机器学习（MACHINE LEARNING）Sklearn全高级使用（看不懂你来打我！）

1 正规化 Normalization

1.1 数据标准化

from sklearn import preprocessing #标准化数据模块
import numpy as np

#建立Array
a = np.array([[10, 2.7, 3.6],
              [-100, 5, -2],
              [120, 20, 40]], dtype=np.float64)

#将normalized后的a打印出
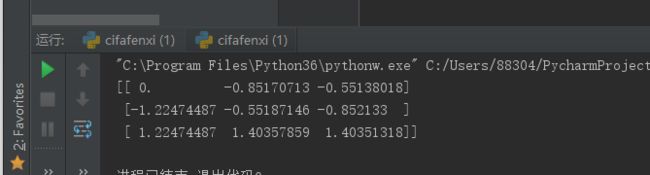
print(preprocessing.scale(a))

1.2 数据标准化对机器学习成效的影响

# 标准化数据模块
from sklearn import preprocessing 
import numpy as np

# 将资料分割成train与test的模块
from sklearn.model_selection import train_test_split

# 生成适合做classification资料的模块 通常用于分类算法。本文用于生成数据集。
from sklearn.datasets.samples_generator import make_classification

# Support Vector Machine中的Support Vector Classifier
from sklearn.svm import SVC #SVC是SVM的一种Type，是用来的做分类的，SVR是SVM的另一种Type，是用来的做回归的。

# 可视化数据的模块
import matplotlib.pyplot as plt



#生成具有2种属性的300笔数据
X, y = make_classification(n_samples=300, n_features=2,n_redundant=0, n_informative=2,
    random_state=22, n_clusters_per_class=1,scale=100)

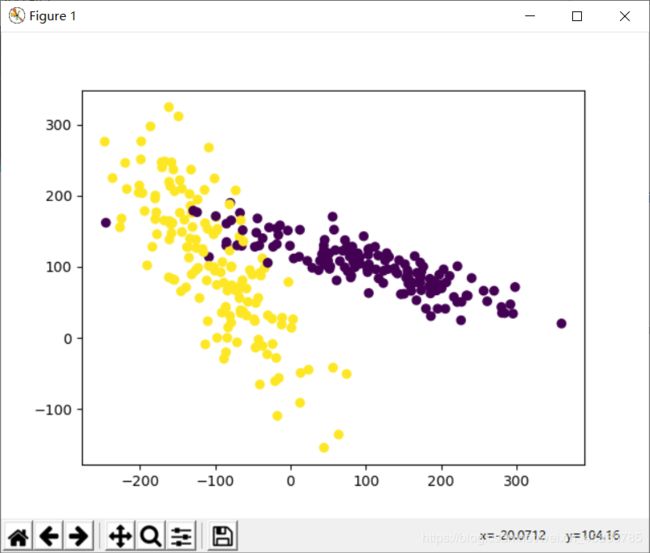
#可视化数据
plt.scatter(X[:, 0], X[:, 1], c=y)
plt.show()

X=preprocessing.scale(X)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
clf = SVC()
clf.fit(X_train, y_train)
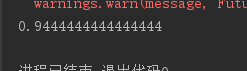
print(clf.score(X_test, y_test))

2 检验神经网络 (Evaluation)

2.1 误差曲线

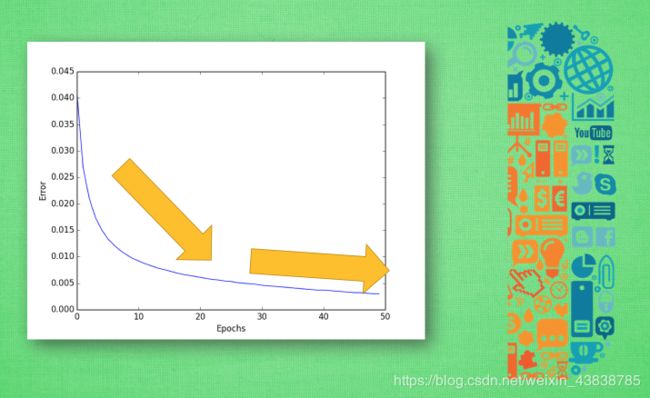
接着, 对于神经网络的评价基本上是基于这30%的测试数据. 想想期末考试虽然花的时间少, 但是占得总成绩肯定要比你平时作业的分多吧. 所以说这30%虽然少, 但是很重要. 然后, 我们就可以开始画图啦! 评价机器学习可以从误差这个值开始, 随着训练时间的变长, 优秀的神经网络能预测到更为精准的答案, 预测误差也会越少 . 到最后能够提升的空间变小, 曲线也趋于水平 . 班上的差生, 从不及格到80分已经不容易啦, 再往上冲刺100分, 就变成了更难的事了. 机器学习也一样. 所以, 如果你的机器学习的误差曲线是这样一条曲线, 那就已经是很不错的学习成果啦.

2.2 准确度曲线

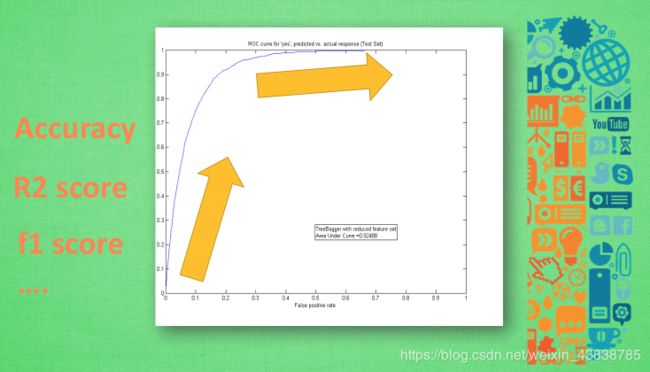
同样, 除了误差曲线, 我们可以看他的精确度曲线. 最好的精度是趋向于100%精确. 比如在神经网络的分类问题中, 100个样本中, 我有90张样本分类正确, 那就是说我的预测精确度是90%. 不过, 不知道大家有没有想过对于回归的问题呢? 怎样看预测值是连续数字的精确度? 这时, 我们可以引用 R2 分数在测量回归问题的精度 . R2给出的最大精度也是100%, 所以分类和回归就都有的统一的精度标准. 除了这些评分标准, 我们还有很多其他的标准, 比如 F1 分数 , 用于测量不均衡数据的精度.

2.3 正规化

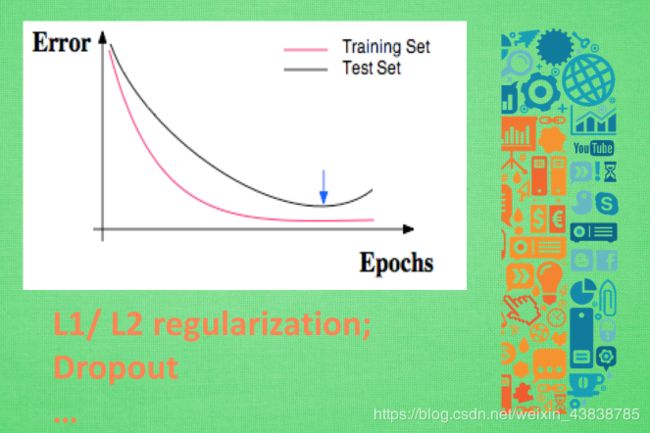
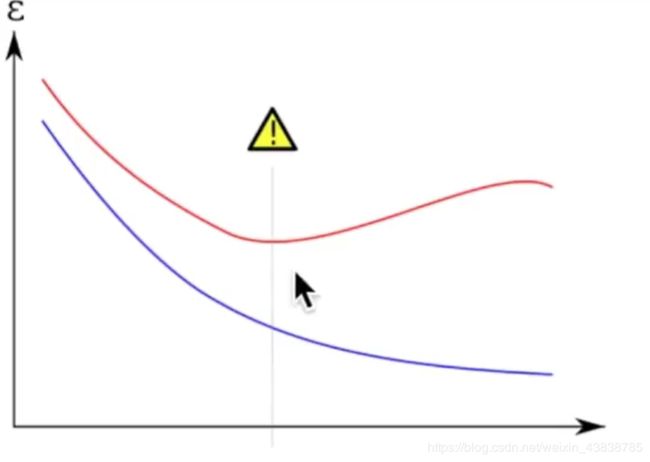
有时候, 意外是猝不及防的, 比如有时候我们明明每一道作业习题都会做, 可是考试分数为什么总是比作业分数低许多? 原来, 我们只复习了作业题,并没有深入, 拓展研究作业反映出来的知识. 这件事情发生在机器学习中, 我们就叫做过拟合. 我们在回到误差曲线, 不过这时我们也把训练误差画出来. 红色的是训练误差, 黑色的是测试误差. 训练时的误差比测试的误差小, 神经网络虽然学习到了知识, 但是对于平时作业太过依赖, 到了考试的时候, 却不能随机应变, 没有成功的把作业的知识扩展开来. 在机器学习中, 解决过拟合也有很多方法 , 比如 l1, l2 正规化, dropout 方法.

2.4 交叉验证

神经网络也有很多参数, 我们怎么确定哪样的参数能够更有效的解决现有的问题呢? 这时, 交叉验证 就是最好的途径了. 交叉验证不仅仅可以用于神经网络的调参, 还能用于其他机器学习方法的调参. 同样是选择你想观看的误差值或者是精确度, 不过横坐标不再是学习时间, 而是你要测试的某一参数 (比如说神经网络层数) . 我们逐渐增加神经层, 然后对于每一个不同层结构的神经网络求出最终的误差或精度, 画在图中. 我们知道, 神经层越多, 计算机所需要消耗的时间和资源就越多, 所以我们只需要找到那个能满足误差要求, 有节约资源的层结构. 比如说误差在0.005一下都能接受 , 那我们就可以采用30层的神经网络结构 .

3 Cross-validation

3.1 Model 基础验证法

from sklearn.datasets import load_iris # iris数据集
from sklearn.model_selection import train_test_split # 分割数据模块
from sklearn.neighbors import KNeighborsClassifier # K最近邻(kNN，k-NearestNeighbor)分类算法

#加载iris数据集
iris = load_iris()
X = iris.data
y = iris.target

#分割数据并
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=4)

#建立模型
knn = KNeighborsClassifier(n_neighbors=5)

#训练模型
knn.fit(X_train, y_train)

#将准确率打印出
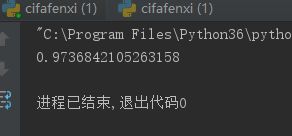
print(knn.score(X_test, y_test))
# 0.973684210526

3.2 Model 交叉验证法(Cross Validation)

cv=5 5个size

一般来说准确率(accuracy)会用于判断分类(Classification)模型的好坏。

from sklearn.datasets import load_iris # iris数据集
from sklearn.model_selection import train_test_split # 分割数据模块
from sklearn.neighbors import KNeighborsClassifier # K最近邻(kNN，k-NearestNeighbor)分类算法
from sklearn.model_selection import cross_val_score # K折交叉验证模块
#加载iris数据集
iris = load_iris()
X = iris.data
y = iris.target

#分割数据并
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=4)

#建立模型
knn = KNeighborsClassifier(n_neighbors=5)

#使用K折交叉验证模块
scores = cross_val_score(knn, X, y, cv=5, scoring='accuracy')

#将5次的预测准确率打印出
print(scores)
# [ 0.96666667  1.          0.93333333  0.96666667  1.        ]

#将5次的预测准确平均率打印出
print(scores.mean())
# 0.973333333333

3.3 以准确率(accuracy)判断（改变n_neighbors）

from sklearn.datasets import load_iris # iris数据集
from sklearn.model_selection import train_test_split # 分割数据模块
from sklearn.neighbors import KNeighborsClassifier # K最近邻(kNN，k-NearestNeighbor)分类算法
from sklearn.model_selection import cross_val_score # K折交叉验证模块
#加载iris数据集
iris = load_iris()
X = iris.data
y = iris.target

#分割数据并
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=4)

import matplotlib.pyplot as plt #可视化模块

#建立测试参数集
k_range = range(1, 31)

k_scores = []

#藉由迭代的方式来计算不同参数对模型的影响，并返回交叉验证后的平均准确率
for k in k_range:
    knn = KNeighborsClassifier(n_neighbors=k)
    scores = cross_val_score(knn, X, y, cv=10, scoring='accuracy') #10个size
    k_scores.append(scores.mean())

#可视化数据
plt.plot(k_range, k_scores)
plt.xlabel('Value of K for KNN')
plt.ylabel('Cross-Validated Accuracy')
plt.show()

从图中可以得知，选择12~18的k值最好。高过18之后，准确率开始下降则是因为过拟合(Over fitting)的问题。

3.4 以平均方差(Mean squared error)

一般来说平均方差(Mean squared error)会用于判断回归(Regression)模型的好坏。

import matplotlib.pyplot as plt
k_range = range(1, 31)
k_scores = []
for k in k_range:
    knn = KNeighborsClassifier(n_neighbors=k)
    loss = -cross_val_score(knn, X, y, cv=10, scoring='mean_squared_error')
    k_scores.append(loss.mean())

plt.plot(k_range, k_scores)
plt.xlabel('Value of K for KNN')
plt.ylabel('Cross-Validated MSE')
plt.show()

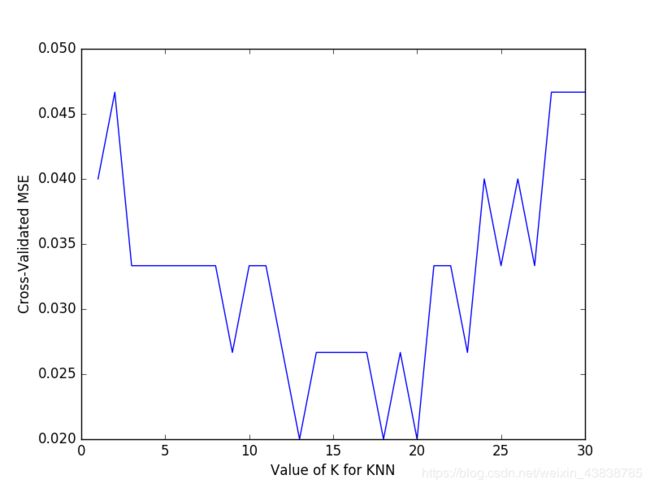
由图可以得知，平均方差越低越好，因此选择13~18左右的K值会最好。

3.5 Learning curve 检视过拟合

mean_squared_error改为neg_mean_squared_error

from sklearn.model_selection import learning_curve #学习曲线模块
from sklearn.datasets import load_digits #digits数据集
from sklearn.svm import SVC #Support Vector Classifier
import matplotlib.pyplot as plt #可视化模块
from sklearn.metrics import mean_squared_error
import numpy as np


digits = load_digits()
X = digits.data
y = digits.target

train_sizes, train_loss, test_loss = learning_curve(
    SVC(gamma=0.001), X, y, cv=10, scoring='neg_mean_squared_error',
    train_sizes=[0.1, 0.25, 0.5, 0.75, 1])

#平均每一轮所得到的平均方差(共5轮，分别为样本10%、25%、50%、75%、100%)
train_loss_mean = -np.mean(train_loss, axis=1)
test_loss_mean = -np.mean(test_loss, axis=1)


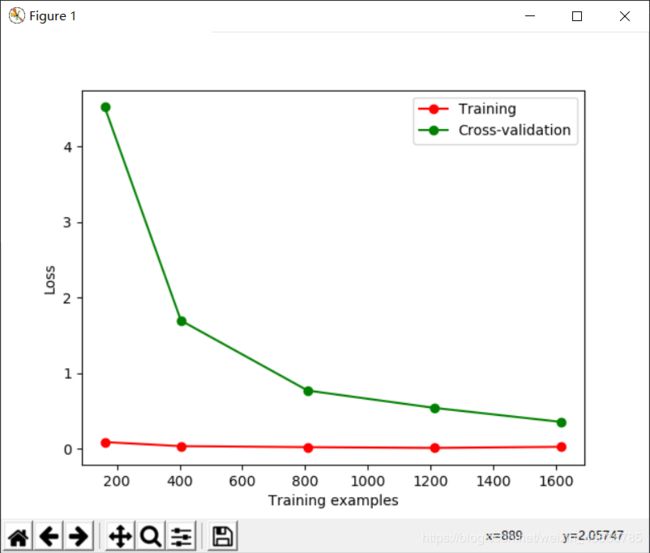
plt.plot(train_sizes, train_loss_mean, 'o-', color="r",
         label="Training")
plt.plot(train_sizes, test_loss_mean, 'o-', color="g",
        label="Cross-validation")

plt.xlabel("Training examples")
plt.ylabel("Loss")
plt.legend(loc="best")
plt.show()

3.6 validation_curve 检视过拟合

, 这一次的 sklearn 中我们用到了sklearn.learning_curve当中的另外一种, 叫做validation_curve,用这一种曲线我们就能更加直观看出改变模型中的参数的时候有没有过拟合(overfitting)的问题了. 这也是可以让我们更好的选择参数的方法.

稍作小修改即可画出图形。这次我们来验证SVC中的一个参数 gamma 在什么范围内能使 model 产生好的结果. 以及过拟合和 gamma 取值的关系.

from sklearn.model_selection import validation_curve #validation_curve模块
from sklearn.datasets import load_digits
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as np

#digits数据集
digits = load_digits()
X = digits.data
y = digits.target

#建立参数测试集
param_range = np.logspace(-6, -2.3, 5)#自己定义

#使用validation_curve快速找出参数对模型的影响
train_loss, test_loss = validation_curve(
    SVC(), X, y, param_name='gamma', param_range=param_range, cv=10, scoring='neg_mean_squared_error')

#平均每一轮的平均方差
train_loss_mean = -np.mean(train_loss, axis=1)
test_loss_mean = -np.mean(test_loss, axis=1)

#可视化图形
plt.plot(param_range, train_loss_mean, 'o-', color="r",
         label="Training")
plt.plot(param_range, test_loss_mean, 'o-', color="g",
        label="Cross-validation")

plt.xlabel("gamma")
plt.ylabel("Loss")
plt.legend(loc="best")
plt.show()

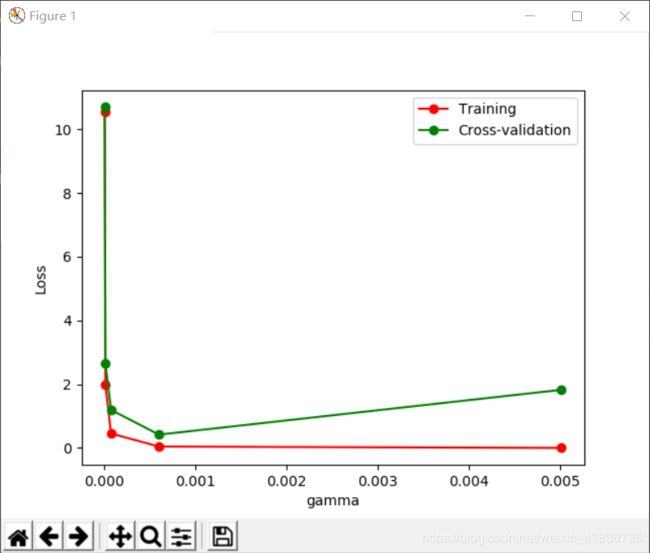
由图中可以明显看到gamma值大于0.001，模型就会有过拟合(Overfitting)的问题。

4 保存模型

4.1 使用 pickle 保存

from sklearn import svm
from sklearn import datasets

clf = svm.SVC()
iris = datasets.load_iris()
X, y = iris.data, iris.target
clf.fit(X,y)


import pickle #pickle模块

#保存Model(注:save文件夹要预先建立，否则会报错)
with open('clf.pickle', 'wb') as f:
    pickle.dump(clf, f)

#读取Model
with open('clf.pickle', 'rb') as f:
    clf2 = pickle.load(f)
    #测试读取后的Model
    print(clf2.predict(X[0:1]))

4.2 用 joblib 保存

from sklearn import svm
from sklearn import datasets

clf = svm.SVC()
iris = datasets.load_iris()
X, y = iris.data, iris.target
clf.fit(X,y)




from sklearn.externals import joblib #jbolib模块

#保存Model(注:save文件夹要预先建立，否则会报错)
joblib.dump(clf, 'clf.pkl')

#读取Model
clf3 = joblib.load('clf.pkl')

#测试读取后的Model
print(clf3.predict(X[0:1]))