飞飞女神的CV课之打好基础（3）
让人又爱又恨的数电阿，我竟然让我のblog整整荒废了一周
不行！不可以！今天就捡起来！~~~冲冲*10^n！
上次说到哪里了，神经网络对吧？
好的，我们今天就来试试
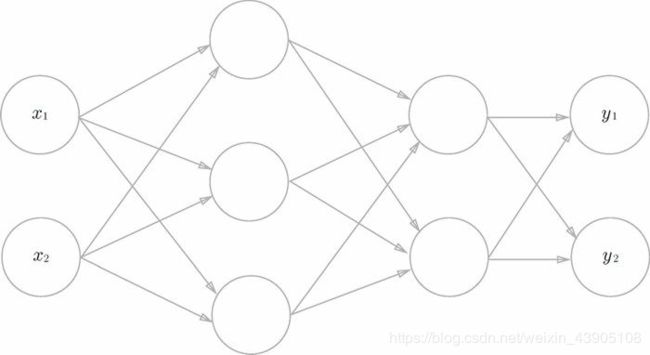
三层神经网络的实现
| 层 | 神经元个数 |
|---|---|
| 第0层（输入层） | 2 |
| 第1层（隐藏层） | 3 |
| 第2层（隐藏层） | 2 |
| 第3层（输出层） | 2 |
符号说明
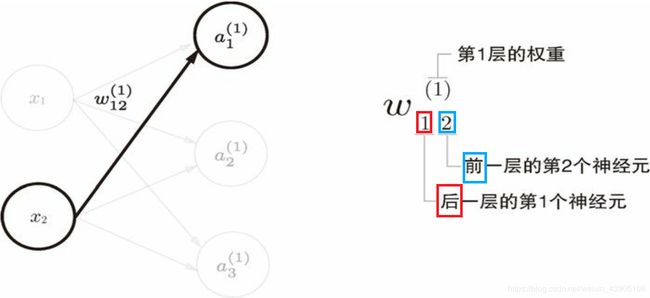
记忆tips：可以理解为它的目的性很强，所以目标神经元是第几个摆在首位。
传递实现
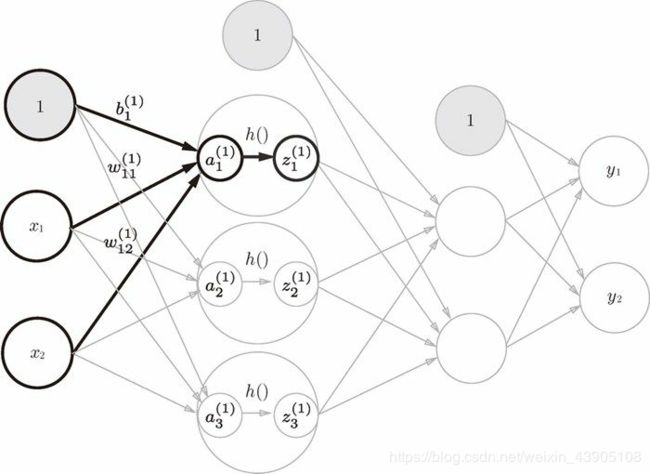
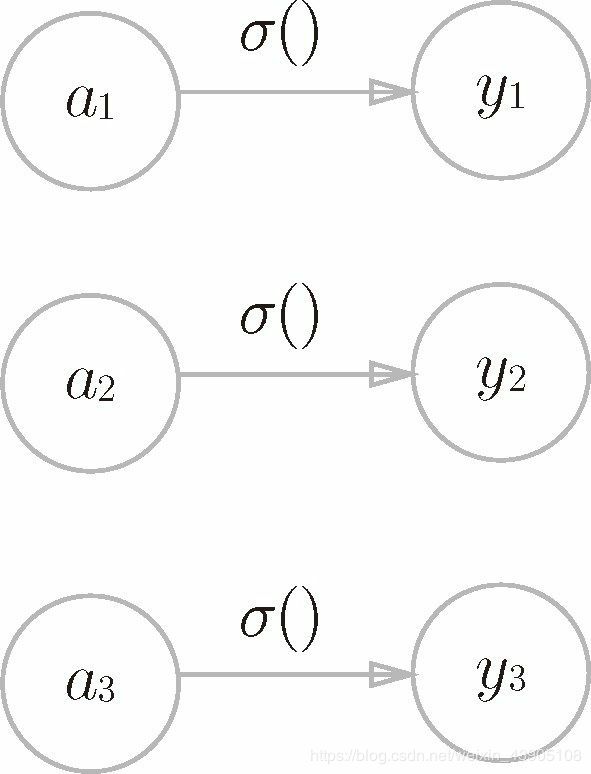
图（1）
这里增加了偏置神经元1，下标只有一个，因为第0层只有一个偏置神经元，所以无所谓从谁出发到1或2或3
根据图（1）可知，应该这样列式子
第一层激活函数计算过程
import numpy as np
#引入sigmoid
import matplotlib.pylab as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
#三层神经网络实现
#第0层到第1层
X = np.array([1.0,0.5])
W1 = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
B1 = np.array([0.1,0.2,0.3])
A1 = np.dot(X,W1) + B1
print(A1)
Z1 = sigmoid(A1)
print(Z1)
第二层激活函数计算过程
#第1层到第2层（接上面）
W2 = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
B2 = np.array([0.1,0.2])
A2 = np.dot(Z1,W2)+B2
Z2 = sigmoid(A2)
print(Z2)
输出层计算过程
#第2层到输出层
def identify_function(x):
return x
W3 = np.array([[0.1,0.3],[0.2,0.4]])
B3 = np.array([0.1,0.2])
A3 = np.dot(Z2,W3) + B3
Y = identify_function(A3)
print(Y)
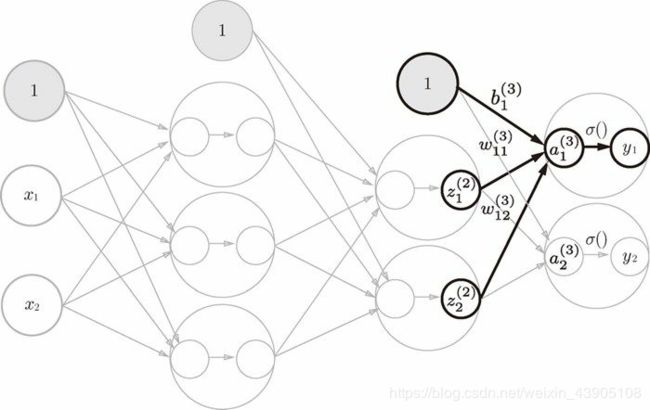
这里定义的identify_function()函数有点像废话，就是“恒等函数”，将其作为输出层的激活函数（用σ()表示，不同于隐藏层的激活函数h()）（其实可以直接写成Y=A3）
代码整理
def identify_function(x):
return x
def init_network():
network={}
network['W1'] = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
network['b1'] = np.array([0.1,0.2,0.3])
network['W2'] = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
network['b2'] = np.array([0.1,0.2])
network['W3'] = np.array([[0.1,0.3],[0.2,0.4]])
network['b3'] = np.array([0.1,0.2])
return network
def forward(network,x):
W1, W2, W3 = network['W1'],network['W2'],network['W3']
b1, b2, b3 = network['b1'],network['b2'],network['b3']
a1 = np.dot(x,W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1,W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2,W3) + b3
y = identify_function(a3)
return y
network = init_network()
x = np.array([1.0,0.5])
y = forward(network,x)
print(y)
输出层设计
机器学习大致可分为回归问题和分类问题，一般而言，回归问题用恒等函数；分类问题用softmax函数。
分类问题：数据属于哪一类的问题（eg:区分图像中的人是男性还是女性）
回归问题：根据某个输入预测一个连续的数值问题（eg:根据一个人的图像预测这个人的体重的问题就是回归问题）
恒等函数
softmax函数
#softmax函数
def softmax(a):
exp_a = np.exp(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
但是，指数存在一个问题——（指数爆炸）溢出，对于计算机，这会出现不可控的后果。在不改变结果的条件下，如何实现正常计算呢？解决办法就是：分子分母同除一个大数。
其实这里的+C是-C，因为指数函数都在x轴上方，所以不用担心会出现负数。
#softmax函数
def softmax(a):
c = np.max(a)
exp_a = np.exp(a - c)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
另外：softmax函数的输出是0.0~1.0之间的实数，而且函数的输出和为1，正是由于这些性质，可以把softmax函数的输出解释为”概率“
import numpy as np
#softmax函数
def softmax(a):
c = np.max(a)
exp_a = np.exp(a - c)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
a = np.array([0.3,2.9,4.0])
y = softmax(a)
print(y)#输出为[0.01821127 0.24519181 0.73659691]
print(np.sum(y))#输出为1.0
可以解释为：y[0]的概率为1.8%，y[1]的概率为24.5%，y[2]的概率为73.7%，可见元素的大小关系并没有改变（a[2]最大，经过softmax函数，还是y[2]最大）。
下期预告：手写数字识别！