CS224N Assignment 2: word2vec (43 Points)

CS224N Assignment 2: word2vec (43 Points)

这一次作业是说如何实现一个 word2vec 的，word2vec 方法的主要思路是 迭代产生结果 。通过每一步的计算损失函数，以及损失函数的梯度，修改当前的单词向量，（这里其实包含了凸优化方法的思路）使用随机梯度下降中的步长以解决最优化问题。

Part 1 Written: Understanding word2vec (23 points)

a) (3 points)

Show that the naive-softmax loss given in Equation (2) is the same as the cross-entropy loss between $y$ and $\hat{y}$ ; i.e., show that:
$$-\sum _{w\in \text{ Vocab }}{y}_w\log \left({\hat{y}}_w\right)=-\log \left({\hat{y}}_o\right)$$
Your answer should be one line.

Proof

$y_w$ 是单位矩阵的一列，因此对于只有中心词 $w_o$ 的位置为 $1$ ，其余为 $0$ ：
$$\begin{gathered} -\sum _{w\in \text{ Vocab }}{y}_w\log \left({\hat{y}}_w\right)=-\sum _{w\in \text{ Vocab } \\ w\ne w_o}{y}_w\log \left({\hat{y}}_w\right)-y_{w_o}\log \left({\hat{y}}_{w_o}\right)=0-log({\hat{y}}_{w_o}) \end{gathered}$$

b) (5 points)

Compute the partial derivative of $J_{\text{naive-softmax }}\left({\mathbf{v}}_c,o,\mathbf{U}\right)$ with respect to $v_c$. Please write your answer in terms of $\mathbf{y},\hat{\mathbf{y}},\text{ and }\mathbf{U}$.

Answer

首先先解释一下：

1. $U$ 代表一个单词作为上下文的坐标；
2. $V$ 代表一个单词作为中心词的坐标；
3. $y$ 是输入（训练集）；
4. $\hat{y}$ 是输出的估计值（对该训练数据的预测）；

$$\begin{array}{rl}\frac{\partial J_{\text{naive-softmax }}}{\partial v_c}& =-\frac{\partial \log Pr(O=o|C=c)}{\partial v_c}=-\frac{\partial \log \left\{\frac{\exp \left({\mathbf{u}}_o^{\top }{\mathbf{v}}_c\right)}{{\sum }_{w\in \mathrm{V}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{b}}\exp \left({\mathbf{u}}_w^{\top }{\mathbf{v}}_c\right)}\right\}}{\partial v_c}\\ & =-\frac{\partial \left[u_o^{\top }{v}_c-\log {\sum }_{w\in \mathrm{V}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{b}}\exp \left(u_w^{\top }{v}_c\right)\right]}{\partial v_c}\\ & =-\left(u_o-\frac{{\sum }_{w\in \text{Vocab}}{u}_w\exp (u_w^{\top }{v}_c)}{{\sum }_{w\in \mathrm{V}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{b}}\exp \left(u_w^{\top }{v}_c\right)}\right)\end{array}$$

将下式代入梯度：
$$P(O=o|C=c)=\frac{\exp \left({\mathbf{u}}_o^{\top }{\mathbf{v}}_c\right)}{{\sum }_{w\in \mathrm{V}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{b}}\exp \left({\mathbf{u}}_w^{\top }{\mathbf{v}}_c\right)}$$
则有
$$\frac{\partial J_{\text{naive-softmax }}}{\partial v_c}=-u_o+\sum _w{u}_{w}P(w|c)$$
因为这里 $u_o=U^{T}y$ 表示取的第 $o$ 个单词的坐标，这里的 $y$ 是独热的，$\sum u_{w}P(w|c)$ 对于给定中心词 $c$ 的概率分布，因此有 $P(w|c)={\hat{y}}_w$ 是我们的预测值，因此上式变为：
$$\frac{\partial J_{\text{naive-softmax }}}{\partial v_c}=U^T(\hat{y}-y)$$

c) (5 points)

Compute the partial derivatives of $J_{\text{naive-softmax }}\left({\mathbf{v}}_c,o,\mathbf{U}\right)$ with respect to each of the ‘outside’ word vectors, $u_w$'s. There will be two cases: when $w=o$, the true ‘outside’ word vector, and $w\ne o$ for all other words. Please write you answer in terms of $\mathbf{y},\hat{\mathbf{y}},\text{ and }{\mathbf{v}}_c$

Answer

1. Case $w=o$
   $$\begin{array}{rl}\frac{\partial J_{\text{naive-softmax }}}{\partial u_o}& =-\frac{\partial \log \left\{\frac{\exp \left({\mathbf{u}}_o^{\top }{\mathbf{v}}_c\right)}{{\sum }_{w\in \mathrm{V}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{b}}\exp \left({\mathbf{u}}_w^{\top }{\mathbf{v}}_c\right)}\right\}}{\partial u_o}\\ & =-\left(v_c-\frac{v_c\exp (u_o^{\top }{v}_c)}{{\sum }_{w\in \mathrm{V}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{b}}\exp \left(u_w^{\top }{v}_c\right)}\right)\\ & =-v_c+v_{c}P(o|c)\end{array}$$
   注意，最后一行是因为求 $u_o$ 的偏导，因此
   $$\frac{\partial {\sum }_{w\ne o}{v}_c\exp (u_w^{\top }{v}_c)}{\partial v_c}=0$$

2. Case $w\ne o$ ，这里避免引发歧义，在求和的地方把符号换成 $i$ 。
   $$\begin{array}{rl}\frac{\partial J_{\text{naive-softmax }}}{\partial u_w}& =-\left(-\frac{v_c\exp (u_w^{\top }{v}_c)}{{\sum }_{i\in \mathrm{V}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{b}}\exp \left(u_i^{\top }{v}_c\right)}\right)\\ & =v_{c}P(w|c)\end{array}$$

因此：
$$\frac{\partial J_{\text{naive-softmax }}}{\partial u_w}=\{\begin{array}{llc}-v_c+v_{c}P(o|c)& & \text{if w=o}\\ v_{c}P(w|c)& & \text{otherwise}\end{array}$$

d) (3 Points)

The sigmoid function is given by Equation;
$$\sigma (x)=\frac{1}{1+e^{-x}}=\frac{e^x}{e^x+1}$$
Please compute the derivative of $\sigma (x)$ with respect to $x$, where $x$ is a scalar. Hint: you may want to write your answer in terms of $\sigma (x)$ .

Answer

$$\frac{d\sigma (x)}{dx}=\frac{e^x(e^x+1)-e^x{e}^x}{(e^x+1{)}^2}=\frac{e^x}{(e^x+1{)}^2}=\sigma (x)(1-\sigma (x))$$

e) (4 points)

Now we shall consider the Negative Sampling loss, which is an alternative to the Naive $softmax$ loss. Assume that K negative samples (words) are drawn from the vocabulary. For simplicity of notation we shall refer to them as $w_1,\cdots ,w_k$ and their outside vectors as $u_1,\dots ,u_K$ . Note that $o\notin \left\{w_1,\cdots ,w_k\right\}$ . For a center word c and an outside word o, the negative sampling loss function is given by:
$$J_{\text{neg-sample }}\left(v_c,o,U\right)=-\log \left(\sigma \left(u_o^{\top }{v}_c\right)\right)-\sum _{k=1}^K\log \left(\sigma \left(-u_k^{\top }{v}_c\right)\right)$$
for a sample $w_1,\cdots ,w_k$ , where $\sigma (.)$ is the sigmoid function.

Please repeat parts (b) and ©, computing the partial derivatives of $J_{\text{neg-sample }}\left(v_c,o,U\right)$ with respect to $v_c,u_o$ and $u_k$ where $k\in [1,K]$ . After you’ve done this, describe with one sentence why thisl oss function is much more effcient to compute than the naive-softmax loss. Note, you should be able to use your solution to part (d) to help compute the necessary gradients here.

Answer

1. With respect to $v_c$
   $$\begin{array}{rl}\frac{\partial J_{\text{neg-sample }}\left(v_c,o,U\right)}{\partial v_c}& =-\frac{\partial \left[\underset{\text{part 1}}{\log \left(\sigma \left(u_o^{\top }{v}_c\right)\right)}+\underset{part2}{\sum _{k=1}^K\log \left(\sigma \left(-u_k^{\top }{v}_c\right)\right)}\right]}{\partial v_c}\end{array}$$
   $\text{part 1}$ 由链式法则：
   $$\frac{\partial \log \left(\sigma (u_o^{\top }{v}_c)\right)}{\partial v_c}=\frac{\sigma (u_o^{\top }{v}_c)(1-\sigma (u_o^{\top }{v}_c))}{\sigma (u_o^{\top }{v}_c)}{u}_o=(1-\sigma (u_o^{\top }{v}_c))u_o$$
   $\text{part 2}$ 由链式法则：
   $$\frac{\partial {\sum }_{k=1}^K\log \left(\sigma \left(-u_k^{\top }{v}_c\right)\right)}{\partial v_c}=\sum _{k=1}^K(1-\sigma (u_k^{\top }{v}_c))u_k$$
   因此：
   $$\begin{array}{rl}\frac{\partial J_{\text{neg-sample }}\left(v_c,o,U\right)}{\partial v_c}& =-\left((1-\sigma (u_o^{\top }{v}_c))u_o-\sum _{k=1}^K(1-\sigma (u_k^{\top }{v}_c))u_k\right)\end{array}$$

2. With respect to $u_o$

   这里注意题干里说的：$o\notin \left\{w_1,\cdots ,w_k\right\}$ ，因此
   $$\begin{array}{rl}\frac{\partial J_{\text{neg-sample }}\left(v_c,o,U\right)}{\partial u_o}& =-\frac{\partial \log \left(\sigma \left(u_o^{\top }{v}_c\right)\right)}{\partial u_o}=-(1-\sigma (u_o^{\top }{v}_c))v_c\end{array}$$

3. With respect to $u_k$
   $$\begin{array}{rl}\frac{\partial J_{\text{neg-sample }}\left(v_c,o,U\right)}{\partial u_k}& =-\frac{\log \left(\sigma \left(-u_k^{\top }{v}_c\right)\right)}{\partial u_k}=-(1-\sigma (-u_k^T{v}_c))v_c\end{array}$$

其实从上面几个导数可以看到一个很好的性质：导数变为乘积，大幅减少运算量，而且保留了原函数中 sigmoid 函数的形式，再次减少这部运算量。

f) (3 points)

Suppose the center word is $c=w_t$ and the context window is $\left[w_{t-m},\dots ,w_{t-1},w_t,w_{t+1},\cdots ,w_{t+m}\right]$ , where m is the context window size. Recall that for the skip-gram version of word2vec, the total loss for the context window is:
$$J_{\text{skip-gram }}\left(v_c,w_{t-m},\dots w_{t+m},U\right)=\sum _{-m\le j\le m,j\ne 0}J\left(v_c,w_{t+j},U\right)$$
Here, $J\left(v_c,w_{t+j},U\right)$ represents an arbitrary loss term for the center word $c=w_t$ and outside word $w_{t+j}$. $J\left(v_c,w_{t+j},U\right)$ could be $J_{\text{naive-softmax }}\left({\mathbf{v}}_c,w_{t+j},\mathbf{U}\right)$ or $J_{\text{neg-sample }}\left({\mathbf{v}}_c,w_{t+j},\mathbf{U}\right)$ , depending on your implementation.

Write down three partial derivatives:
$$\begin{array}{l}\frac{\partial J}{\partial U}=\partial {\mathbf{J}}_{\text{skip-gram }}\left({\mathbf{v}}_c,w_{t-m},\dots w_{t+m},\mathbf{U}\right)/\partial \mathbf{U}\\ \frac{\partial J}{\partial v_c}=\partial {\mathbf{J}}_{\text{skip-gram }}\left({\mathbf{v}}_c,w_{t-m},\dots w_{t+m},\mathbf{U}\right)/\partial {\mathbf{v}}_c\\ \frac{\partial J}{\partial v_w}=\partial {\mathbf{J}}_{\text{skip-gram }}\left({\mathbf{v}}_c,w_{t-m},\dots w_{t+m},\mathbf{U}\right)/\partial {\mathbf{v}}_w\text{ when }w\ne c\end{array}$$

Answer

这里用 neg-sample 来表述所有的损失函数。

对 $U$ 求偏导：
$$\frac{\partial J}{\partial U}=\sum _j\frac{\partial J((v_c,w_{t+j},U))}{\partial U}$$
对 $v_c$ 求偏导：
$$\begin{array}{rl}\frac{\partial J}{\partial v_c}& =\sum _{-m\le j\le m,j\ne 0}\frac{\partial J\left(v_c,w_{t+j},U\right)}{\partial v_c}\\ & =-\sum _{-m\le j\le m,j\ne 0}\left((1-\sigma (u_o^{\top }{v}_c))u_o-\sum _{k=1}^K(1-\sigma (u_k^{\top }{v}_c))u_k\right)\end{array}$$
这个函数是不包含 $v_w$ 这个变量的，因此：
$$\begin{array}{rl}\frac{\partial J}{\partial v_w}& =\sum _{-m\le j\le m,j\ne 0}\frac{\partial J\left(v_c,w_{t+j},U\right)}{\partial v_w}=0\end{array}$$

Part 2 Coding: Implementing word2vec (20 points)

使用随机梯度下降法（stochastic gradient
descent）进行单词向量的训练。首先需要安装一下环境，控制台 cd 到 a2 的目录下输入：

conda env create -f env.yml
conda activate a2

做完之后输入：

conda deactivate

这一个 part 里，注意使用 numpy 程序包使整个代码执行效率更高，因为执行时间也被考虑在最终结果中。

a) (12 points)

We will start by implementing methods in word2vec.py. First, implement the sigmoid method, which takes in a vector and applies the sigmoid function to it. Then implement the softmax loss and gradient in the naiveSoftmaxLossAndGradient method, and negative sampling loss and gradient in the negSamplingLossAndGradient method. Finally, fill in the implementation for the skip-gram model in the skipgram method. When you are done, test your implementation by running python word2vec.py.

Answer:

这部分是对 Word2Vec 的一个实现。

Step 1 实现 Sigmoid 函数

首先，先实现 sigmoid 函数，输入是 np.array 这个数据结构，输出也应该是一个向量。根据定义：

$$\sigma (x)=\frac{1}{1+\exp (-x)}$$

题目要求用一行代码实现，代码实现如下：

def sigmoid(x):
    """
    Compute the sigmoid function for the input here.
    Arguments:
    x -- A scalar or numpy array.
    Return:
    s -- sigmoid(x)
    """

    ### YOUR CODE HERE (~1 Line)
    s = 1 / (np.exp(-x) + 1)
    ### END YOUR CODE

    return s

稍微自己可以测试一下：

sigmoid(np.array([-1,0,1]))
>>> array([0.26894142, 0.5       , 0.73105858])

Step 2 实现 naiveSoftmaxLossAndGradient 函数

在文件夹中有一个 utils 程序包中，有 utils.py 文件，里面包含 softmax 这个函数，我们在实现中需要调用这个函数。

根据之前数学的推导：

1. $\hat{y}=\left[\begin{array}{c}P(1|c)\\ ⋮\\ P(w|c)\\ ⋮\\ P(|V||c)\end{array}\right]=U^{T}y$
2. $J=-y_o\log {\hat{y}}_o=-\log {\hat{y}}_o$ 获得损失函数的值
3. 因为在这里：
   $$\frac{\partial J}{\partial v_c}=U^{\top }(\hat{y}-y)\in {\mathbb{R}}^{|V|\times 1}，\frac{\partial J}{\partial U}=(\hat{y}-y{)}^{\top }{v}_c\in {\mathbb{R}}^{|V|\times n}$$
   为了避免重复工作量，因此先计算出 $\hat{y}-y$ 然后按公式进行编写就可以了。

Remark： 在计算关于 $U$ 的梯度的时候，要注意添加新坐标轴，不然输出的是一个 $1$ 维的常数。

def naiveSoftmaxLossAndGradient(
    centerWordVec,
    outsideWordIdx,
    outsideVectors,
    dataset
):
    """ Naive Softmax loss & gradient function for word2vec models

    Implement the naive softmax loss and gradients between a center word's 
    embedding and an outside word's embedding. This will be the building block
    for our word2vec models.

    Arguments:
    centerWordVec -- numpy ndarray, center word's embedding
                    in shape (word vector length, )
                    (v_c in the pdf handout)
    outsideWordIdx -- integer, the index of the outside word
                    (o of u_o in the pdf handout)
    outsideVectors -- outside vectors is
                    in shape (num words in vocab, word vector length) 
                    for all words in vocab (U in the pdf handout)
    dataset -- needed for negative sampling, unused here.

    Return:
    loss -- naive softmax loss
    gradCenterVec -- the gradient with respect to the center word vector
                     in shape (word vector length, )
                     (dJ / dv_c in the pdf handout)
    gradOutsideVecs -- the gradient with respect to all the outside word vectors
                    in shape (num words in vocab, word vector length) 
                    (dJ / dU)
    """

    ### YOUR CODE HERE (~6-8 Lines)
    
    ### Please use the provided softmax function (imported earlier in this file)
    ### This numerically stable implementation helps you avoid issues pertaining
    ### to integer overflow. 
    U, vc, o = outsideVectors, centerWordVec, outsideWordIdx
    yhat = softmax(np.dot(U, vc))
    loss = -np.log(yhat[o])
    yhat[o] -= 1#(yhat-y)
    gradCenterVec = np.dot(U.T, yhat)
    gradOutsideVecs = np.dot(yhat[:, np.newaxis], vc[:, np.newaxis].T)
    ### END YOUR CODE

    return loss, gradCenterVec, gradOutsideVecs

然后来测试一下：

>>> Reloaded modules: utils, utils.gradcheck, utils.utils
	==== Gradient check for skip-gram with naiveSoftmaxLossAndGradient ====
	Gradient check passed!. Read the docstring of the `gradcheck_naive` method in utils.gradcheck.py to understand what the gradient check does.

Step 3 实现 negSamplingLossAndGradient 函数

同理，按公式一行行进行实现，公式如下：

$$\begin{gathered} J_{\text{neg-sample }}\left(v_c,o,U\right)=-\log \left(\sigma \left(u_o^{\top }{v}_c\right)\right)-\sum _{k=1}^K\log \left(\sigma \left(-u_k^{\top }{v}_c\right)\right) \\ \frac{\partial J_{\text{neg-sample }}\left(v_c,o,U\right)}{\partial v_c}=-\left(\left(1-\sigma \left(u_o^{\top }{v}_c\right)\right)u_o-\sum _{k=1}^K\left(1-\sigma \left(u_k^{\top }{v}_c\right)\right)u_k\right) \\ \frac{\partial J_{\text{neg-sample }}\left(v_c,o,U\right)}{\partial u_o}=-\frac{\partial \log \left(\sigma \left(u_o^{\top }{v}_c\right)\right)}{\partial u_o}=-\left(1-\sigma \left(u_o^{\top }{v}_c\right)\right)v_c \\ \frac{\partial J_{\text{neg-sample }}\left(v_c,o,U\right)}{\partial u_k}=-\frac{\log \left(\sigma \left(-u_k^{\top }{v}_c\right)\right)}{\partial u_k}=-\left(1-\sigma \left(-u_k^T{v}_c\right)\right)v_c \end{gathered}$$

这里由于对不同的索引下标，计算 sigmoid 函数时的参数是不同的，因此只能构造一个 for 循环进行实现。

def negSamplingLossAndGradient(
    centerWordVec,
    outsideWordIdx,
    outsideVectors,
    dataset,
    K=10
):
    """ Negative sampling loss function for word2vec models

    Implement the negative sampling loss and gradients for a centerWordVec
    and a outsideWordIdx word vector as a building block for word2vec
    models. K is the number of negative samples to take.

    Note: The same word may be negatively sampled multiple times. For
    example if an outside word is sampled twice, you shall have to
    double count the gradient with respect to this word. Thrice if
    it was sampled three times, and so forth.

    Arguments/Return Specifications: same as naiveSoftmaxLossAndGradient
    """

    # Negative sampling of words is done for you. Do not modify this if you
    # wish to match the autograder and receive points!
    negSampleWordIndices = getNegativeSamples(outsideWordIdx, dataset, K)
    indices = [outsideWordIdx] + negSampleWordIndices
    
    ### YOUR CODE HERE (~10 Lines)
    U, vc, o = outsideVectors, centerWordVec, outsideWordIdx
    gradCenterVec, gradOutsideVecs = np.zeros(vc.shape), np.zeros(U.shape)
    ### Please use your implementation of sigmoid in here.
    yhat = sigmoid(np.dot(U, vc))
    loss = -np.log(yhat[o])
    yhat[o] -= 1
    gradCenterVec += U[o] * yhat[o]
    gradOutsideVecs[o] += vc * yhat[o]
    for k in range(len(indices)):
        if indices[k] != o:
            neg = indices[k]
            negsig = sigmoid(-np.dot(U[neg], vc))
            loss -= np.log(negsig)
            gradCenterVec += np.multiply(U[neg], 1-negsig)
            gradOutsideVecs[neg] += np.multiply(vc, 1-negsig)
    ### END YOUR CODE

    return loss, gradCenterVec, gradOutsideVecs

这部分没有测试代码，具体对不对在后面比较两种损失函数的而效率的时候进行比较。

Step 4 实现 Skip-Gram

根据上述 f) 题的结果来进行求和计算，公式如下：

$$\begin{gathered} J_{\text{skip-gram }}\left(v_c,w_{t-m},\dots w_{t+m},U\right)=\sum _{-m\le j\le m,j\ne 0}J\left(v_c,w_{t+j},U\right) \\ \frac{\partial J}{\partial U}=\sum _j\frac{\partial J((v_c,w_{t+j},U))}{\partial U} \\ \frac{\partial J}{\partial v_c}=\sum _{-m\le j\le m,j\ne 0}\frac{\partial J\left(v_c,w_{t+j},U\right)}{\partial v_c} \\ \frac{\partial J}{\partial v_w}=\sum _{-m\le j\le m,j\ne 0}\frac{\partial J\left(v_c,w_{t+j},U\right)}{\partial v_w}=0,\text{这部不用纳入计算} \end{gathered}$$

def skipgram(currentCenterWord, windowSize, outsideWords, word2Ind,
             centerWordVectors, outsideVectors, dataset,
             word2vecLossAndGradient = naiveSoftmaxLossAndGradient):
    """ Skip-gram model in word2vec

    Implement the skip-gram model in this function.

    Arguments:
    currentCenterWord -- a string of the current center word
    windowSize -- integer, context window size
    outsideWords -- list of no more than 2*windowSize strings, the outside words
    word2Ind -- a dictionary that maps words to their indices in
              the word vector list
    centerWordVectors -- center word vectors (as rows) is in shape 
                        (num words in vocab, word vector length) 
                        for all words in vocab (V in pdf handout)
    outsideVectors -- outside vectors is in shape 
                        (num words in vocab, word vector length) 
                        for all words in vocab (U in the pdf handout)
    word2vecLossAndGradient -- the loss and gradient function for
                               a prediction vector given the outsideWordIdx
                               word vectors, could be one of the two
                               loss functions you implemented above.

    Return:
    loss -- the loss function value for the skip-gram model
            (J in the pdf handout)
    gradCenterVec -- the gradient with respect to the center word vector
                     in shape (word vector length, )
                     (dJ / dv_c in the pdf handout)
    gradOutsideVecs -- the gradient with respect to all the outside word vectors
                    in shape (num words in vocab, word vector length) 
                    (dJ / dU)
    """

    loss = 0.0
    gradCenterVecs = np.zeros(centerWordVectors.shape)
    gradOutsideVectors = np.zeros(outsideVectors.shape)

    ### YOUR CODE HERE (~8 Lines)
    U, vc = outsideVectors, centerWordVectors
    cur = vc[word2Ind[currentCenterWord]]
    for i in outsideWords:
        outside_i, cur_i = word2Ind[i], word2Ind[currentCenterWord]
        loss_i, gradVC_i, gradU_i = word2vecLossAndGradient(cur, outside_i, U,dataset)
        loss += loss_i
        gradCenterVecs[cur_i] += gradVC_i
        gradOutsideVectors += gradU_i
        
    ### END YOUR CODE
    
    return loss, gradCenterVecs, gradOutsideVectors

第一部分代码测试：

>>> Reloaded modules: utils, utils.gradcheck, utils.utils
	==== Gradient check for skip-gram with naiveSoftmaxLossAndGradient ====
	Gradient check passed!. Read the docstring of the `gradcheck_naive` method in utils.gradcheck.py to understand what the gradient check does.
	======Skip-Gram with naiveSoftmaxLossAndGradient Test Cases======
	The first test passed!
	The second test passed!
	The third test passed!
	All 3 tests passed!
	==== Gradient check for skip-gram with negSamplingLossAndGradient ====
	Gradient check passed!. Read the docstring of the `gradcheck_naive` method in utils.gradcheck.py to understand what the gradient check does.
	======Skip-Gram with negSamplingLossAndGradient======
	The first test passed!
	The second test passed!
	The third test passed!
	All 3 tests passed!

结果通过。

b) (4 points)

Complete the implementation for your SGD optimizer in the sgd method of sgd.py. Test your implementation by running python sgd.py.

Answer：

这部分叫我们实现随机梯度下降法。看得一头雾水，实际上知道是怎么做之后有点想骂人。注意注释里到这里有一句话：

"""
Arguments:
    f -- the function to optimize, it should take a single
         argument and yield two outputs, a loss and the gradient
         with respect to the arguments
"""

用这个函数就能算出残差以及梯度。梯度下降法的主要思路是求出当前点的下降方向（梯度）然后顺着这个下降方向向下 搜索 下一个迭代点。前后两个迭代点的距离称为步长，常见 搜索 的方法有回溯直线搜索、精确直线搜索。这里的步长是题目这里给我们的，直接用就可以了。因此我们需要插入的两句代码如下:

loss, grad = f(x)
x = x - step * grad

执行结果如下：

>>> Running sanity checks...
	iter 100: 0.004578
	iter 200: 0.004353
	iter 300: 0.004136
	iter 400: 0.003929
	iter 500: 0.003733
	iter 600: 0.003546
	iter 700: 0.003369
	iter 800: 0.003200
	iter 900: 0.003040
	iter 1000: 0.002888
	test 1 result: 8.414836786079764e-10
	iter 100: 0.000000
	iter 200: 0.000000
	iter 300: 0.000000
	iter 400: 0.000000
	iter 500: 0.000000
	iter 600: 0.000000
	iter 700: 0.000000
	iter 800: 0.000000
	iter 900: 0.000000
	iter 1000: 0.000000
	test 2 result: 0.0
	iter 100: 0.041205
	iter 200: 0.039181
	iter 300: 0.037222
	iter 400: 0.035361
	iter 500: 0.033593
	iter 600: 0.031913
	iter 700: 0.030318
	iter 800: 0.028802
	iter 900: 0.027362
	iter 1000: 0.025994
	test 3 result: -2.524451035823933e-09
	----------------------------------------
	ALL TESTS PASSED
	----------------------------------------

c) (4 points)

Show time! Now we are going to load some real data and train word vectors with everything you just implemented! We are going to use the Stanford Sentiment Treebank (SST) dataset to train word vectors, and later apply them to a simple sentiment analysis task. You will need to fetch the datasets fi rst. To do this, run sh get datasets.sh. There is no additional code to write for this part; just run python run.py.

Answer：

个人建议直接官网上下载下来，再解压下来导入到 utils 这个文件夹中比较好，直接用 sh get datasets.sh 我个人是没有成功过。

运算结果：

>>> ...
	iter 39970: 9.330720
	iter 39980: 9.410215
	iter 39990: 9.418270
	iter 40000: 9.367644
	sanity check: cost at convergence should be around or below 10
	training took 16580 seconds

一共跑了40000次迭代，跑了我电脑四个半小时（官方说的1到2个小时如果你不是今年新买的电脑的话，千万别信，实在太久了）。收敛性其实也满足了它的要求：低于 10 即可。

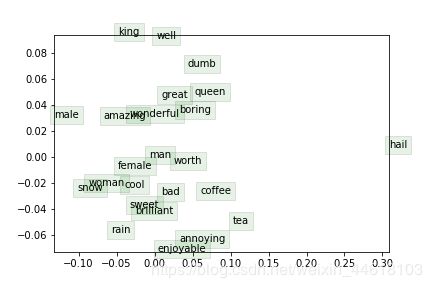
然后这是他选出一些单词的二维坐标的示意图。（这个数据集应该也在不断更新中，你们如果看到跟我不一样，应该是训练集版本的问题，只需要满足 sanity check 就没问题了）这里本来每个单词是10维的，只不过这里降维显示了而已

观察结果：

1. 用法相同的单词很多都被聚类在一起：（比如：great, wonderful, boring 还有 man, female）它们之间的意思不一定相同，但是他们词性是相同的，出现在同一个上下文的概率也很高。
2. 某些归并的效果并不是特别好，因为可以看到 man 和 male 这两个词之间的距离还是较远，然而 female 和 woman 这两个词之间的距离很近，这可能是由于训练集的原因。
3. 其实随机梯度下降法在跑的时候，有些时候损失函数其实是上升的，这可能是由于随机算法的原因，如果选择最速梯度下降法，收敛速度可能会得到一定的提升。