记一次成功做出四道题的 Leetcode 单周赛 —— 第 181 场单周赛及其题目详解
记一次成功做出四道题的 Leetcode 单周赛 —— 第 181 场单周赛及其题目详解
5364. 按既定顺序创建目标数组(3分)
题目来源:https://leetcode-cn.com/problems/create-target-array-in-the-given-order/
给你两个整数数组 nums 和 index。你需要按照以下规则创建目标数组:
- 目标数组 target 最初为空。
- 按从左到右的顺序依次读取 nums[i] 和 index[i],在 target 数组中的下标 index[i] 处插入值 nums[i] 。
- 重复上一步,直到在 nums 和 index 中都没有要读取的元素。
请你返回目标数组。
题目保证数字插入位置总是存在。
示例 1:
输入:nums = [0,1,2,3,4], index = [0,1,2,2,1]
输出:[0,4,1,3,2]
解释:
nums index target
0 0 [0]
1 1 [0,1]
2 2 [0,1,2]
3 2 [0,1,3,2]
4 1 [0,4,1,3,2]
题解
解题思想特别简单,只需要顺序遍历,并模拟流程给出操作就可以了,不需要特别去想别的。时间复杂度 O ( N ) O(N) O(N),空间复杂度 O ( N ) O(N) O(N)。
class Solution(object):
def createTargetArray(self, nums, index):
target = []
n = len(nums)
for i in range(n):
target.insert(index[i], nums[i])
return target
5178. 四因数
来源:https://leetcode-cn.com/problems/four-divisors/
给你一个整数数组 nums,请你返回该数组中恰有四个因数的这些整数的各因数之和。如果数组中不存在满足题意的整数,则返回 0 。
示例:
输入:nums = [21,4,7]
输出:32
解释:
21 有 4 个因数:1, 3, 7, 21
4 有 3 个因数:1, 2, 4
7 有 2 个因数:1, 7
答案仅为 21 的所有因数的和。
题解
没有什么特别的,只需要从两侧向内找每个元素的因数,并判断是否大于4即可。时间复杂度 O ( N M ) O(N\sqrt{M}) O(NM), M M M 为最大的元素。
class Solution(object):
def sumFourDivisors(self, nums):
def Get(x):
lst = []
for i in range(1, int(pow(x, 0.5))+1):
if not x % i:
lst.append(i)
temp = x // i
if temp != lst[-1]:
lst.append(temp)
return lst
count = 0
for i in nums:
temp = Get(i)
# print(i, temp)
if len(temp) == 4:
count += sum(temp)
return count
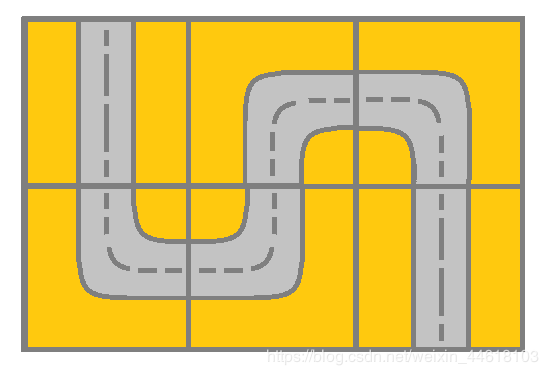
5366. 检查网格中是否存在有效路径
来源:https://leetcode-cn.com/problems/check-if-there-is-a-valid-path-in-a-grid/
给你一个 m x n 的网格 grid。网格里的每个单元都代表一条街道。grid[i][j] 的街道可以是:
- 表示连接左单元格和右单元格的街道。
- 表示连接上单元格和下单元格的街道。
- 表示连接左单元格和下单元格的街道。
- 表示连接右单元格和下单元格的街道。
- 表示连接左单元格和上单元格的街道。
- 表示连接右单元格和上单元格的街道。
输入:grid = [[2,4,3],[6,5,2]]
输出:true
解释:如图所示,你可以从 (0, 0) 开始,访问网格中的所有单元格并到达 (m - 1, n - 1) 。
题解
一般碰到这种网格问题,我个人更倾向于使用BFS算法(只是因为DFS我写的不熟练)。因此我们需要的问题划分为如下两个子问题:
- 如何判定下一步该往哪里走:这里使用的是BFS的思路,按发现顺序,将每个点都走一次。
- 如何判定最终能否到达终点:只需要判断是否能够发现右下角的点即可。
这里需要引入一个小技巧:对于每个走过的点,都标记为 “b”,这只是我个人喜好,你可以标记为任何原本不出现在矩阵中的记号。
对于第一个问题,因为每块方格中的数值决定了它有哪两个方向可以走,因此,一共有 6 × 2 = 12 6\times 2=12 6×2=12 种情况,判断是否能够继续走的程序如下:
def edges(pos, grid):
r, c = pos
m, n = len(grid), len(grid[0])
lst = []
if grid[r][c] == 1:
# 向右
if c < n-1 and grid[r][c+1] in {1, 3, 5}:
lst.append((r, c+1))
# 向左
if c > 0 and grid[r][c-1] in {1, 4, 6}:
lst.append((r, c-1))
elif grid[r][c] == 2:
# 向下
if r < m-1 and grid[r+1][c] in {2, 5, 6}:
lst.append((r+1, c))
# 向上
if r > 0 and grid[r-1][c] in {2, 3, 4}:
lst.append((r-1, c))
elif grid[r][c] == 3:
# 向下
if r < m-1 and grid[r+1][c] in {2, 5, 6}:
lst.append((r+1, c))
# 向左
if c > 0 and grid[r][c-1] in {1, 4, 6}:
lst.append((r, c-1))
elif grid[r][c] == 4:
# 向下
if r < m-1 and grid[r+1][c] in {2, 5, 6}:
lst.append((r+1, c))
# 向右
if c < n-1 and grid[r][c+1] in {1, 3, 5}:
lst.append((r, c+1))
elif grid[r][c] == 5:
# 向上
if r > 0 and grid[r-1][c] in {2, 3, 4}:
lst.append((r-1, c))
# 向左
if c > 0 and grid[r][c-1] in {1, 4, 6}:
lst.append((r, c-1))
elif grid[r][c] == 6:
# 向上
if r > 0 and grid[r-1][c] in {2, 3, 4}:
lst.append((r-1, c))
# 向右
if c < n-1 and grid[r][c+1] in {1, 3, 5}:
lst.append((r, c+1))
return lst
接下来是我们的BFS部分:上述提到的小技巧,就是走过一个点,把他标记为 “b”,只需要一个while循环即可,如果再也走不动了,就退出while循环,进行下一步:
gray = [(0, 0)]
m, n = len(grid), len(grid[0])
if m == 1 and n == 1: return True
while gray:
cur = gray.pop(0)
sur = edges(cur, grid)
if not sur:
break
for s in sur:
gray.append(s)
if s == (m-1, n-1):
return True
grid[cur[0]][cur[1]] = "b"
return False
因此整个函数如下所示:
class Solution(object):
def hasValidPath(self, grid):
def edges(pos, grid):
r, c = pos
m, n = len(grid), len(grid[0])
lst = []
if grid[r][c] == 1:
# 向右
if c < n-1 and grid[r][c+1] in {1, 3, 5}:
lst.append((r, c+1))
# 向左
if c > 0 and grid[r][c-1] in {1, 4, 6}:
lst.append((r, c-1))
elif grid[r][c] == 2:
# 向下
if r < m-1 and grid[r+1][c] in {2, 5, 6}:
lst.append((r+1, c))
# 向上
if r > 0 and grid[r-1][c] in {2, 3, 4}:
lst.append((r-1, c))
elif grid[r][c] == 3:
# 向下
if r < m-1 and grid[r+1][c] in {2, 5, 6}:
lst.append((r+1, c))
# 向左
if c > 0 and grid[r][c-1] in {1, 4, 6}:
lst.append((r, c-1))
elif grid[r][c] == 4:
# 向下
if r < m-1 and grid[r+1][c] in {2, 5, 6}:
lst.append((r+1, c))
# 向右
if c < n-1 and grid[r][c+1] in {1, 3, 5}:
lst.append((r, c+1))
elif grid[r][c] == 5:
# 向上
if r > 0 and grid[r-1][c] in {2, 3, 4}:
lst.append((r-1, c))
# 向左
if c > 0 and grid[r][c-1] in {1, 4, 6}:
lst.append((r, c-1))
elif grid[r][c] == 6:
# 向上
if r > 0 and grid[r-1][c] in {2, 3, 4}:
lst.append((r-1, c))
# 向右
if c < n-1 and grid[r][c+1] in {1, 3, 5}:
lst.append((r, c+1))
return lst
gray = [(0, 0)]
m, n = len(grid), len(grid[0])
if m == 1 and n == 1: return True
while gray:
cur = gray.pop(0)
sur = edges(cur, grid)
if not sur:
break
for s in sur:
gray.append(s)
if s == (m-1, n-1):
return True
grid[cur[0]][cur[1]] = "b"
return False
5367. 最长快乐前缀
来源:https://leetcode-cn.com/problems/longest-happy-prefix/
「快乐前缀」是在原字符串中既是 非空 前缀也是后缀(不包括原字符串自身)的字符串。
给你一个字符串 s,请你返回它的 最长快乐前缀。
如果不存在满足题意的前缀,则返回一个空字符串。
示例 1:
输入:s = "level"
输出:"l"
解释:不包括 s 自己,一共有 4 个前缀("l", "le", "lev", "leve")和
4 个后缀("l", "el", "vel", "evel")。最长的既是前缀也是后缀的字符串是 "l" 。
题解
这题为什么能被冠上 困难 的标签?是因为这道题对时间的要求比较高。常见的切片是不可能在规定时间完成的。因此需要引入另一个技术。
在数据可视化中,有一项技术叫做快速局部直方图技术。大体思想是:统计了一块区域的内部的信息之后,在更新下一个点的时候,只需要更新两条边界线上的数据,就能得到当前块的信息。
具体这个想法怎么应用到这道题上来的呢?首先我们统计整个字符串的信息,利用 https://leetcode-cn.com/problems/compress-string-lcci/ 的方式存储字符串,与之不同的是,我写入的是一个列表(因为pop更加方便)。
在统计了整个字符串之后,复制一份,其中一份从头进行删减操作;另一份从尾向前删减,直到两个列表是相等的,如果相等,恢复字符串即可。
import copy
class Solution(object):
def longestPrefix(self, s):
lst = []
for i in s:
if not lst or lst[-2] != i:
lst.append(i)
lst.append(1)
elif lst[-2] == i:
lst[-1] += 1
l = lst
r = copy.copy(lst)
for i in range(len(s)):
if l[-1] == 1:
l.pop()
l.pop()
else:
l[-1] -= 1
if r[1] == 1:
r.pop(0)
r.pop(0)
else:
r[1] -= 1
if l == r:
break
s = ""
for i in range(0, len(l), 2):
s += l[i]*(l[i+1])
return s
整体来说,这次周赛做下来其实是比较顺利的,因为题目里出现都是自己熟悉的知识点。当然这也是我第一次能够在规定时间内做出四道题,排名前7%,在此留念。