机器学习：K-Means聚类、DBSCAN聚类

1、K-Means聚类

K-Means聚类算法的思想简单，对于给定的样本集，按照样本之间的距离大小，将样本划分为K个簇，让簇内的点尽可能紧密的连在一起，簇间的距离尽可能大。
假设簇划分为$(C_1,C_2,...,C_k)$，则损失函数为：
$E={\sum }_{i=1}^k{\sum }_{x\in C_i}{\Vert x-{\mu }_i\Vert }_2^2$

1.1K-Means算法流程
步骤1：初始化聚类个数k和k个初始质心
步骤2：计算每个样本到k个质心的欧式距离，根据距离大小，将样本划分到与之距离最近的簇中
步骤3：更新每个簇的质心
步骤4：重复步骤2-3，直到满足收敛要求（质心不再变化）

1.2K-Means优缺点
优点：原理简单，实现容易，聚类效果中上，时间复杂度O(N)
缺点：对离群点，噪声点敏感，需要设定聚类个数，结果不一定是全局最优，只能保证局部最优，无法识别具有复杂形状的簇

# KMeans
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import numpy as np

# 生成数据
x, y = make_blobs(n_samples=100, random_state=42)

# kmeans聚类
kmeans = KMeans(n_clusters=3).fit(x)

# 可视化
x_min, x_max = x[:, 0].min() - 1, x[:, 0].max() + 1
y_min, y_max = x[:, 1].min() - 1, x[:, 1].max() + 1

xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02))
z = kmeans.predict(np.c_[xx.ravel(), yy.ravel()])

zz = z.reshape(xx.shape)

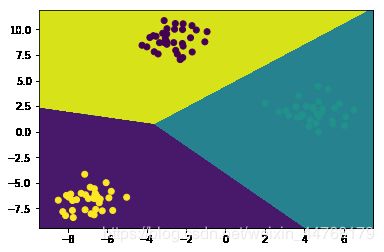
plt.contourf(xx, yy, zz)
plt.scatter(x[:, 0], x[:, 1], c=y)
plt.show()

2、DBSCAN聚类

2.1基本概念
DBSCAN(Density-Based Spatial Clustering of Application with Noise)是一种典型的基于密度的聚类算法，在DBSCAN算法中将数据点分为一下三类：
核心点。在半径Eps内含有超过MinPts数目的点
边界点。在半径Eps内点的数量小于MinPts，但是落在核心点的邻域内
噪音点。既不是核心点也不是边界点的点

在这里有两个量，一个是半径Eps，另一个是指定的数目MinPts。
一些其他的概念
(1)Eps邻域。简单来讲就是与点$p$的距离小于等于Eps的所有的点的集合，可以表示为$N_{Eps}(p)$。
(2)直接密度可达。如果$p$在核心对象的Eps邻域内，则称对象$p$从对象$q$出发是直接密度可达的。
(3)密度可达。对于对象链：$p_1,p_2,...,p_n$，$p_{i+1}$是从$p_i$关于Eps和MinPts直接密度可达的，则对象是从对象关于Eps和MinPts密度可达的。

2.2DBSCAN算法流程图
步骤1：将所有样本标记为核心点、边界点或者噪声点
步骤2：删除噪声点
步骤3：为距离在Eps之内的所有核心点之间赋予一条边
步骤4：每组连通的核心点形成一个簇
步骤5：将每个边界点指派到一个与之关联的核心点的簇中

# DBSCAN密度聚类
from sklearn.datasets import make_circles
from sklearn.cluster import DBSCAN
import matplotlib.pyplot as plt

# 随机生成数据
x, y = make_circles(n_samples=1000, noise=0.03, random_state=42, factor=0.7)

# 密度聚类
db = DBSCAN(eps=0.1, min_samples=10).fit(x)

# 可视化原始数据
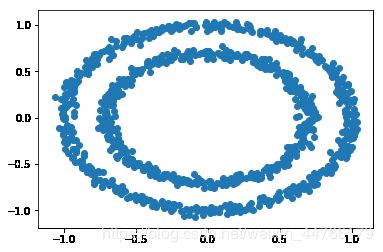
plt.scatter(x[:, 0], x[:, 1])
plt.show()

# 聚类后可视化
y_pred = db.fit_predict(x)
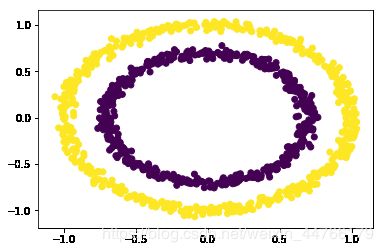
plt.scatter(x[:, 0], x[:, 1], c=y_pred)
plt.show()

K-Means和DBSCAN的区别

• K-Means和DBSCAN都是将每个样本指派到单个簇的划分算法，但K-Means一般聚类所有对象，而DBSCAN会丢弃被它识别的噪声点
• K-Means使用簇的基本原型概念，而DBSCAN使用基于密度的概念
• K-Means很难处理非球型的簇和不同大小的簇，DBSCAN可以处理不同大小的簇和球型的簇，并且不太受噪声点和离群点的影响
• K-Means可以用于稀疏的高维数据，DBSCAN通常在这类数据上的性能表现差，因为对于高维数据，传统的欧式距离密度定义不能很好的处理它
• K-Means需要指定质心个数，DBSCAN需要指定邻域半径Eps和最少点数MinPts