深入理解梯度下降法

对于随机梯度和批量梯度的介绍可参考这一篇文章，作者总结的很好：https://www.cnblogs.com/lliuye/p/9451903.html

但看了很多，总觉得理解的还不是很清楚，所以这篇文献我想换个角度，用自己的话来梳理和总结一下。

假设数据集如下，有三个样本，具体取值不重要

一：$\{x_1^{(1)},x_2^{(1)}，y^{(1)}\}$

二：$\{x_1^{(2)},x_2^{(2)}，y^{(2)}\}$

三：$\{x_1^{(3)},x_2^{(3)}，y^{(3)}\}$

假设函数为：
​ $$h(x^{(i)})={\theta }_0{x}_1^{(i)}+{\theta }_1{x}_1^{(i)}$$

全部样本的损失函数为：
​ $$J({\theta }_0,{\theta }_1)=\frac{1}{2m}\sum _{i=1}^m(h(x^{(i)})-y^i{)}^2$$

其中$m$为样本数，$i$为参数个数

注意这里的损失函数是对全部样本的损失函数求和后再平均的，即均方误差。多除2是为了好约掉求导后的2，

所以这里的损失函数可以理解为全部样本的平均损失函数。

单个样本的损失函数为：
​ $$loss=\frac{1}{2}(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$

对于一个二维的样本数据，其生成的损失函数的图像都如图曲面所示：

对此图像的理解可以如下：针对一个给定的样本，即$x_1$,$x_2$已知，带入$h(x^{(i)})={\theta }_0{x}_1^{(i)}+{\theta }_1{x}_1^{(i)}$计算预测值,而其中${\theta }_0,{\theta }_1$是未知的，也是需要我们求的。我们采用了最简单粗暴的方法来列举了各种${\theta }_0,{\theta }_1$的可能组合，针对每一组组合，计算对应的$h(x^{(i)})$和$J({\theta }_0,{\theta }_1)$,于是就得到了大量的$J({\theta }_0,{\theta }_1)$值，在一个三维空间中标志出来，就形成了上图所示的一个曲面。

梯度下降法的三个要素：步长、初始值和归一化

梯度下降法就是在决定了步长和初始值后，从初始值开始，计算其梯度（梯度是一个向量，具有大小和方向），沿着其负梯度方向进行下降。最终的目的是为了找到损失函数的最小值，即上图曲面中的最低点（很多时候找的是极小值，只有凸函数才有全局最优，上图就是凸函数形成的曲面）。最低点对应的参数组合$({\theta }_0,{\theta }_1)$就是我们想要的最佳参数值。

每一个样本都对应着一个这样的曲面，所以三个样本会有三个这样的曲面由于$x_1和x_2$的取值不同，所以生成的$J({\theta }_0,{\theta }_1)$曲面肯定不一样，最后找到的最佳$({\theta }_0,{\theta }_1)$也会不一样。

假设三个样本生成的三个曲面如下（可以想象成是不一样的，我偷懒复制一下），分别命名为A、B、C

好，接下来就可以进一步理解随机梯度下降和批量梯度下降了

1.随机梯度下降法

在随机梯度下降中，我们知道每次随机采用一个样本数据进行梯度下降（不管怎么选，全部样本还是都得用完），即每次只选择A、B、C三个曲面中的一个，计算梯度更新$\theta$

SGD迭代一次的过程如下：

（1）计算单个样本的损失函数为：
​ $$J^{(i)}({\theta }_0,{\theta }_1)=\frac{1}{2}(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$

（2）对损失函数个各个θ求偏导,即求某一方向上的梯度：
​ $$\frac{{\Delta }^{J(i)}({\theta }_0,{\theta }_1)}{{\theta }_j}=(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$$

（3）最后，更新各个θ：
​ $${\theta }_j:={\theta }_j-\alpha (h_{\theta }(x^{(i))}-y^{(i)})x_j^{(i)}$$

2.批量梯度下降法

相较于随机梯度下降每次迭代只计算一个样本的损失函数，批量梯度下降法每次迭代都要计算全部样本的损失函数，这是两者主要的区别点，即步骤（1）的区别，另外两步是一样的。

BGD迭代一次的过程如下：

（1）计算全部样本的损失函数为：
​ $$J^{(i)}({\theta }_0,{\theta }_1)=\frac{1}{2m}\sum _{i=1}^m(h(x^{(i)})-y^i{)}^2$$

（2）对损失函数个各个θ求偏导,即求某一方向上的梯度：
​ $$\frac{{\Delta }^{J(i)}({\theta }_0,{\theta }_1)}{{\theta }_j}=(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$$

（3）最后，更新各个θ：
​ $${\theta }_j:={\theta }_j-\alpha (h_{\theta }(x^{(i))}-y^{(i)})x_j^{(i)}$$

小结BGD和SGD：

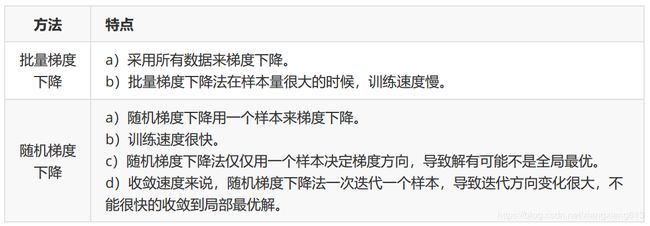
随机梯度下降法比批量梯度下降法快，比如一个30W数量的样本集，批量梯度下降法设置迭代10次，则损失函数的计算量为$10\ast 30W$次，随机梯度下降法每次选择一个样本计算损失函数，则计算量为$30W\ast 1次$，明显快得多。