深度学习还不够好,安全的人工智能需要贝叶斯深度学习
深度学习还不够好,安全的人工智能需要贝叶斯深度学习
Deep Learning Is Not Good Enough, We Need Bayesian Deep Learning for Safe AI
理解模型的不确定度(uncertainty)是机器学习的关键。但能够理解不确定度的传统机器学习方法(如高斯过程,Gaussian processes),无法应用于如图像、视频等高维数据。深度学习(deep learning)能够高效处理该类数据,但其难以对不确定度建模。
本文旨在:
(1)给出不确定度的类型,并建模。
(2)使用不确定度为多任务深度学习模型减重。
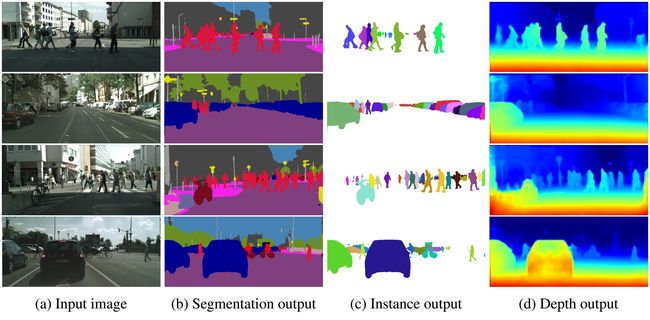
图像深度估计示例:(1)图像深度估计贝叶斯神经网络输入样本;(2)深度估计输出;(3)估计的不确定度。
不确定度类型(types of uncertainty)
认知不确定度和随机不确定度(epistemic and aleatoric uncertainty)
认知不确定度(epistemic uncertainty)
认知不确定度(epistemic uncertainty)描述了根据给定训练集得到的模型的不确定度。这种不确定度可通过提供用足够多的数据消除,也被称为模型不确定度(model uncertainty)。
认知不确定度对下列应用至关重要:
(1)安全至上的应用,认知不确定度是理解模型泛化能力的关键;
(2)训练数据稀疏的小数据集。
随机不确定度(aleatoric uncertainty)
随机不确定度(aleatoric uncertainty)描述了关于数据无法解释的信息的不确定度。例如,图像的随机不确定度可以归因于遮挡、缺乏视觉特征或过度曝光区域等。这种不确定度可通过以更高精度观察所有解释性变量(explanatory variables)的能力来消除。
随机不确定度对下列应用至关重要:
(1)海量数据(large data),此时认知不确定度几乎被完全消除;
(2)实时(real-time)应用,取消蒙特卡罗采样(Monte Carlo sampling),用输入数据的确知函数(a deterministic function of the input data)表示随机模型(aleatoric models)。
随机不确定度可细分分为两个类:
(1)数据相关(data-dependant)不确定度或异方差不确定度(heteroscedastic uncertainty):依赖于输入数据且模型输出为预测的随机不确定度。
(2)任务相关(task-dependant)不确定度或同方差不确定度(homoscedastic uncertainty):不依赖于输入数据的的随机不确定度;对于所有输入数据,它为常量;它在不同的任务之间变化;它不是模型输出;它可用来描述依赖任务的不确定度。
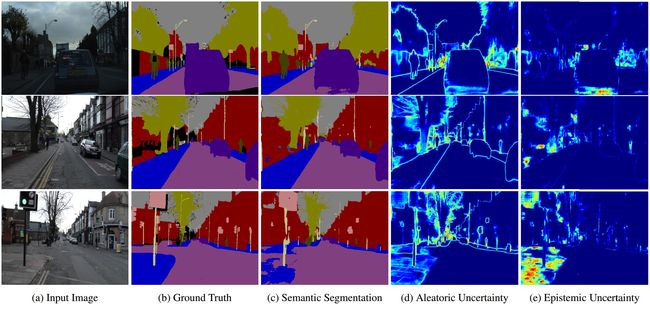
示例:图像语义分割中的随机不确定度与认知不确定度,随机不确定度给出了有噪标签的物体边界。第三行给出模型对人行道(footpath)不熟悉时,图像语义分割失败的案例,其对应的认知不确定度变大。
贝叶斯深度学习(Bayesian deep learning)
贝叶斯深度学习(Bayesian deep learning)是深度学习(deep learning)与贝叶斯概率论(Bayesian probability theory)的交叉领域,它给出了深度学习架构的不确定度评估原理(principled uncertainty estimates)。
贝叶斯深度学习利用深度学习的层次表示(hierarchical representation power)对复杂任务进行建模,同时对复杂的多模态后验分布(multi-modal posterior distributions)进行推理。贝叶斯深度学习模型(Bayesian deep learning models)通过模型权重的分布(distributions over model weights),或学习直接映射输出概率(a direct mapping to probabilistic outputs)对不确定度进行估计。
- 改变损失函数对异方差随机不确定度(heteroscedastic aleatoric uncertainty)建模
异方差不确定度是输入数据的函数,因此可通过学习输入到输出的确知映射(a deterministic mapping)对其预测。对于回归问题(regression tasks),可定义类似欧式距离( L 2 L_2 L2, L = ∥ y − y ^ ∥ 2 \mathcal{L}=\|y − \hat{y}\|^2 L=∥y−y^∥2)的损失函数:
(1) L = ∥ y − y ^ ∥ 2 2 σ 2 + 1 2 log σ 2 \mathcal{L}=\frac{{\|y − \hat{y}\|}^2}{2 \sigma^2} + \frac{1}{2}\log \sigma^2 \tag{1} L=2σ2∥y−y^∥2+21logσ2(1)
其中, y ^ \hat{y} y^和 σ 2 \sigma^2 σ2分别为模型预测的均值和方差。当模型预测误差很大时,上式通过增加不确定度减小残差项(residual term); 1 2 log σ 2 \frac{1}{2}\log \sigma^2 21logσ2为惩罚项,防止不确定度(unceitainty term)趋于无穷大。
同方差不确定度建模方法类似,但不确定度参数不再是模型输出,而是可优化的自由参数。
认知不确定度的建模需要计算模型及其参数的分布,常用方法为蒙特卡罗采样(Monte Carlo dropout sampling),用伯努利分布(Bernoulli distribution)抽取网络权值。用dropout训练模型,在测试阶段,用不同的随机dropout掩模从网络中随机采样则,输出分布的统计量(statistics)能够反映模型的认知不确定度。
| Training Data | Testing Data | Aleatoric Variance | Epistemic Variance |
|---|---|---|---|
| Trained on dataset #1 | Tested on dataset #1 | 0.485 | 2.78 |
| Trained on 25% dataset #1 | Tested on dataset #1 | 0.506 | 7.73 |
| Trained on dataset #1 | Tested on dataset #2 | 0.461 | 4.87 |
| Trained on 25% dataset #1 | Tested on dataset #2 | 0.388 | 15.0 |
结果表明:当训练数据集很小或者测试数据与训练数据差异显著时,认知不确定度急剧增大;而随机不确定度保持相对不变,其原因在于它是用同一传感器在相同问题上测试的。
多任务学习的不确定度(uncertainty for multi-task learning)
通过共享表示(a shared representation)学习多个目标,多任务学习(multi-task learning)旨提高学习效率和预测精度。多任务学习对限制计算复杂度的系统至关重要。将所有任务合并到一个模型中能够减少计算量,允许系统实时运行(run in real-time)。
大多数多任务模型使用损失加权和训练不同的任务,其性能严重依赖于各子任务损失间的相对权值,权值调整极其困难,因而限制了多任务学习的应用。
由于同方差不确定度与输入数据无关,因此可将其解释为任务不确定度(task uncertainty),用来加权多任务学习模型的损失。
场景理解算法(scene understanding algorithms)必须能够同时理解场景的几何形状和其语义(多任务学习问题)。在深度感知问题中,由于多任务学习能够使用其它子任务(如语义分割)的线索(and vice versa),因此它提高了深度感知的平顺性和准确性。
挑战(some challenging research questions)
- 实时认知不确定度(real-time epistemic uncertainty)
- 贝叶斯深度学习的基准(benchmarks for Bayesian deep learning models):如何定量测量不确定度(measure the calibration of uncertainty)
- 描术多模型分布的推理技术(better inference techniques to capture multi-modal distributions)
参考文献:
A. Kendall & Y. Gal, What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision?, 2017
A. Kendall, Y. Gal & R. Cipolla, Multi-Task Learning Using Uncertainty to Weigh Losses for Scene Geometry and Semantics, 2017