十、简单线性回归的python实现(详解)
4. 简单线性回归的python实现
点击标题即可获取源代码和笔记
4.1 导入相关包
import numpy as np
import pandas as pd
import random
import matplotlib as mpl
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['simhei'] # 显示中文
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
%matplotlib inline # 将图片嵌套在输出框中显示,而不是单独跳出一张图片
4.2 导入数据集并探索数据
ex0 = pd.read_table("./datas/ex0.txt",header=None)
ex0.head()
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 1.0 | 0.067732 | 3.176513 |
| 1 | 1.0 | 0.427810 | 3.816464 |
| 2 | 1.0 | 0.995731 | 4.550095 |
| 3 | 1.0 | 0.738336 | 4.256571 |
| 4 | 1.0 | 0.981083 | 4.560815 |
ex0.shape
(200, 3)
ex0.describe()
| 0 | 1 | 2 | |
|---|---|---|---|
| count | 200.0 | 200.000000 | 200.000000 |
| mean | 1.0 | 0.488319 | 3.835601 |
| std | 0.0 | 0.292943 | 0.503443 |
| min | 1.0 | 0.014855 | 3.078132 |
| 25% | 1.0 | 0.234368 | 3.452775 |
| 50% | 1.0 | 0.466573 | 3.839350 |
| 75% | 1.0 | 0.730712 | 4.247613 |
| max | 1.0 | 0.995731 | 4.692514 |
4.3 构建辅助函数
ex0.iloc[:,-1].values
array([3.176513, 3.816464, 4.550095, 4.256571, 4.560815, 3.929515,
3.52617 , 3.156393, 3.110301, 3.149813, 3.476346, 4.119688,
4.282233, 3.486582, 4.655492, 3.965162, 3.5149 , 3.125947,
4.094115, 3.476039, 3.21061 , 3.190612, 4.631504, 4.29589 ,
3.085028, 3.44808 , 3.16744 , 3.364266, 3.993482, 3.891471,
3.143259, 3.114204, 3.851484, 4.621899, 4.580768, 3.620992,
3.580501, 4.618706, 3.676867, 4.641845, 3.175939, 4.26498 ,
3.558448, 3.436632, 3.831052, 3.182853, 3.498906, 3.946833,
3.900583, 4.238522, 4.23308 , 3.521557, 3.203344, 4.278105,
3.555705, 3.502661, 3.859776, 4.275956, 3.916191, 3.587961,
3.183004, 4.225236, 4.231083, 4.240544, 3.222372, 4.021445,
3.567479, 3.56258 , 4.262059, 3.208813, 3.169825, 4.193949,
3.491678, 4.533306, 3.550108, 4.636427, 3.557078, 3.552874,
3.494159, 3.206828, 3.195266, 4.221292, 4.413372, 4.184347,
3.742878, 3.201878, 4.648964, 3.510117, 3.274434, 3.579622,
3.489244, 4.237386, 3.913749, 3.22899 , 4.286286, 4.628614,
3.239536, 4.457997, 3.513384, 3.729674, 3.834274, 3.811155,
3.598316, 4.692514, 4.604859, 3.864912, 3.184236, 3.500796,
3.743365, 3.622905, 4.310796, 3.583357, 3.901852, 3.233521,
3.105266, 3.865544, 4.628625, 4.231213, 3.791149, 3.968271,
4.25391 , 3.19471 , 3.996503, 3.904358, 3.503976, 4.557545,
3.699876, 4.613614, 3.140401, 4.206717, 3.969524, 4.476096,
3.136528, 4.279071, 3.200603, 3.299012, 3.209873, 3.632942,
3.248361, 3.995783, 3.563262, 3.649712, 3.951845, 3.145031,
3.181577, 4.637087, 3.404964, 3.873188, 4.633648, 3.154768,
4.623637, 3.078132, 3.913596, 3.221817, 3.938071, 3.880822,
4.176436, 4.648161, 3.332312, 4.240614, 4.532224, 4.557105,
4.610072, 4.636569, 4.229813, 3.50086 , 4.245514, 4.605182,
3.45434 , 3.180775, 3.38082 , 4.56502 , 3.279973, 4.554241,
4.63352 , 4.281037, 3.844426, 3.891601, 3.849728, 3.492215,
4.592374, 4.632025, 3.75675 , 3.133555, 3.567919, 4.363382,
3.560165, 4.564305, 4.215055, 4.174999, 4.58664 , 3.960008,
3.529963, 4.213412, 3.908685, 3.585821, 4.374394, 3.213817,
3.952681, 3.129283])
ex0.iloc[:,-1].values.shape
(200,)
(ex0.iloc[:,-1].values).T
array([3.176513, 3.816464, 4.550095, 4.256571, 4.560815, 3.929515,
3.52617 , 3.156393, 3.110301, 3.149813, 3.476346, 4.119688,
4.282233, 3.486582, 4.655492, 3.965162, 3.5149 , 3.125947,
4.094115, 3.476039, 3.21061 , 3.190612, 4.631504, 4.29589 ,
3.085028, 3.44808 , 3.16744 , 3.364266, 3.993482, 3.891471,
3.143259, 3.114204, 3.851484, 4.621899, 4.580768, 3.620992,
3.580501, 4.618706, 3.676867, 4.641845, 3.175939, 4.26498 ,
3.558448, 3.436632, 3.831052, 3.182853, 3.498906, 3.946833,
3.900583, 4.238522, 4.23308 , 3.521557, 3.203344, 4.278105,
3.555705, 3.502661, 3.859776, 4.275956, 3.916191, 3.587961,
3.183004, 4.225236, 4.231083, 4.240544, 3.222372, 4.021445,
3.567479, 3.56258 , 4.262059, 3.208813, 3.169825, 4.193949,
3.491678, 4.533306, 3.550108, 4.636427, 3.557078, 3.552874,
3.494159, 3.206828, 3.195266, 4.221292, 4.413372, 4.184347,
3.742878, 3.201878, 4.648964, 3.510117, 3.274434, 3.579622,
3.489244, 4.237386, 3.913749, 3.22899 , 4.286286, 4.628614,
3.239536, 4.457997, 3.513384, 3.729674, 3.834274, 3.811155,
3.598316, 4.692514, 4.604859, 3.864912, 3.184236, 3.500796,
3.743365, 3.622905, 4.310796, 3.583357, 3.901852, 3.233521,
3.105266, 3.865544, 4.628625, 4.231213, 3.791149, 3.968271,
4.25391 , 3.19471 , 3.996503, 3.904358, 3.503976, 4.557545,
3.699876, 4.613614, 3.140401, 4.206717, 3.969524, 4.476096,
3.136528, 4.279071, 3.200603, 3.299012, 3.209873, 3.632942,
3.248361, 3.995783, 3.563262, 3.649712, 3.951845, 3.145031,
3.181577, 4.637087, 3.404964, 3.873188, 4.633648, 3.154768,
4.623637, 3.078132, 3.913596, 3.221817, 3.938071, 3.880822,
4.176436, 4.648161, 3.332312, 4.240614, 4.532224, 4.557105,
4.610072, 4.636569, 4.229813, 3.50086 , 4.245514, 4.605182,
3.45434 , 3.180775, 3.38082 , 4.56502 , 3.279973, 4.554241,
4.63352 , 4.281037, 3.844426, 3.891601, 3.849728, 3.492215,
4.592374, 4.632025, 3.75675 , 3.133555, 3.567919, 4.363382,
3.560165, 4.564305, 4.215055, 4.174999, 4.58664 , 3.960008,
3.529963, 4.213412, 3.908685, 3.585821, 4.374394, 3.213817,
3.952681, 3.129283])
(ex0.iloc[:,-1].values).T.shape
(200,)
'''
函数功能:输入DF数据集(最后一列为标签),返回特征矩阵和标签矩阵
'''
def get_Mat(dataSet):
xMat = np.mat(dataSet.iloc[:,:-1].values)
yMat = np.mat(dataSet.iloc[:,-1].values).T
return xMat,yMat
# 查看函数运行结果
xMat,yMat = get_Mat(ex0)
xMat.shape
(200, 2)
xMat
matrix([[1. , 0.067732],
[1. , 0.42781 ],
[1. , 0.995731],
[1. , 0.738336],
[1. , 0.981083],
[1. , 0.526171],
[1. , 0.378887],
[1. , 0.033859],
[1. , 0.132791],
[1. , 0.138306],
[1. , 0.247809],
[1. , 0.64827 ],
[1. , 0.731209],
[1. , 0.236833],
[1. , 0.969788],
[1. , 0.607492],
[1. , 0.358622],
[1. , 0.147846],
[1. , 0.63782 ],
[1. , 0.230372],
[1. , 0.070237],
[1. , 0.067154],
[1. , 0.925577],
[1. , 0.717733],
[1. , 0.015371],
[1. , 0.33507 ],
[1. , 0.040486],
[1. , 0.212575],
[1. , 0.617218],
[1. , 0.541196],
[1. , 0.045353],
[1. , 0.126762],
[1. , 0.556486],
[1. , 0.901144],
[1. , 0.958476],
[1. , 0.274561],
[1. , 0.394396],
[1. , 0.87248 ],
[1. , 0.409932],
[1. , 0.908969],
[1. , 0.166819],
[1. , 0.665016],
[1. , 0.263727],
[1. , 0.231214],
[1. , 0.552928],
[1. , 0.047744],
[1. , 0.365746],
[1. , 0.495002],
[1. , 0.493466],
[1. , 0.792101],
[1. , 0.76966 ],
[1. , 0.251821],
[1. , 0.181951],
[1. , 0.808177],
[1. , 0.334116],
[1. , 0.33863 ],
[1. , 0.452584],
[1. , 0.69477 ],
[1. , 0.590902],
[1. , 0.307928],
[1. , 0.148364],
[1. , 0.70218 ],
[1. , 0.721544],
[1. , 0.666886],
[1. , 0.124931],
[1. , 0.618286],
[1. , 0.381086],
[1. , 0.385643],
[1. , 0.777175],
[1. , 0.116089],
[1. , 0.115487],
[1. , 0.66351 ],
[1. , 0.254884],
[1. , 0.993888],
[1. , 0.295434],
[1. , 0.952523],
[1. , 0.307047],
[1. , 0.277261],
[1. , 0.279101],
[1. , 0.175724],
[1. , 0.156383],
[1. , 0.733165],
[1. , 0.848142],
[1. , 0.771184],
[1. , 0.429492],
[1. , 0.162176],
[1. , 0.917064],
[1. , 0.315044],
[1. , 0.201473],
[1. , 0.297038],
[1. , 0.336647],
[1. , 0.666109],
[1. , 0.583888],
[1. , 0.085031],
[1. , 0.687006],
[1. , 0.949655],
[1. , 0.189912],
[1. , 0.844027],
[1. , 0.333288],
[1. , 0.427035],
[1. , 0.466369],
[1. , 0.550659],
[1. , 0.278213],
[1. , 0.918769],
[1. , 0.886555],
[1. , 0.569488],
[1. , 0.066379],
[1. , 0.335751],
[1. , 0.426863],
[1. , 0.395746],
[1. , 0.694221],
[1. , 0.27276 ],
[1. , 0.503495],
[1. , 0.067119],
[1. , 0.038326],
[1. , 0.599122],
[1. , 0.947054],
[1. , 0.671279],
[1. , 0.434811],
[1. , 0.509381],
[1. , 0.749442],
[1. , 0.058014],
[1. , 0.482978],
[1. , 0.466776],
[1. , 0.357767],
[1. , 0.949123],
[1. , 0.41732 ],
[1. , 0.920461],
[1. , 0.156433],
[1. , 0.656662],
[1. , 0.616418],
[1. , 0.853428],
[1. , 0.133295],
[1. , 0.693007],
[1. , 0.178449],
[1. , 0.199526],
[1. , 0.073224],
[1. , 0.286515],
[1. , 0.182026],
[1. , 0.621523],
[1. , 0.344584],
[1. , 0.398556],
[1. , 0.480369],
[1. , 0.15335 ],
[1. , 0.171846],
[1. , 0.867082],
[1. , 0.223855],
[1. , 0.528301],
[1. , 0.890192],
[1. , 0.106352],
[1. , 0.917886],
[1. , 0.014855],
[1. , 0.567682],
[1. , 0.068854],
[1. , 0.603535],
[1. , 0.53205 ],
[1. , 0.651362],
[1. , 0.901225],
[1. , 0.204337],
[1. , 0.696081],
[1. , 0.963924],
[1. , 0.98139 ],
[1. , 0.987911],
[1. , 0.990947],
[1. , 0.736021],
[1. , 0.253574],
[1. , 0.674722],
[1. , 0.939368],
[1. , 0.235419],
[1. , 0.110521],
[1. , 0.218023],
[1. , 0.869778],
[1. , 0.19683 ],
[1. , 0.958178],
[1. , 0.972673],
[1. , 0.745797],
[1. , 0.445674],
[1. , 0.470557],
[1. , 0.549236],
[1. , 0.335691],
[1. , 0.884739],
[1. , 0.918916],
[1. , 0.441815],
[1. , 0.116598],
[1. , 0.359274],
[1. , 0.814811],
[1. , 0.387125],
[1. , 0.982243],
[1. , 0.78088 ],
[1. , 0.652565],
[1. , 0.87003 ],
[1. , 0.604755],
[1. , 0.255212],
[1. , 0.730546],
[1. , 0.493829],
[1. , 0.257017],
[1. , 0.833735],
[1. , 0.070095],
[1. , 0.52707 ],
[1. , 0.116163]])
# xMat.A ,把matrix变为array类型
xMat.A[:,1]
array([0.067732, 0.42781 , 0.995731, 0.738336, 0.981083, 0.526171,
0.378887, 0.033859, 0.132791, 0.138306, 0.247809, 0.64827 ,
0.731209, 0.236833, 0.969788, 0.607492, 0.358622, 0.147846,
0.63782 , 0.230372, 0.070237, 0.067154, 0.925577, 0.717733,
0.015371, 0.33507 , 0.040486, 0.212575, 0.617218, 0.541196,
0.045353, 0.126762, 0.556486, 0.901144, 0.958476, 0.274561,
0.394396, 0.87248 , 0.409932, 0.908969, 0.166819, 0.665016,
0.263727, 0.231214, 0.552928, 0.047744, 0.365746, 0.495002,
0.493466, 0.792101, 0.76966 , 0.251821, 0.181951, 0.808177,
0.334116, 0.33863 , 0.452584, 0.69477 , 0.590902, 0.307928,
0.148364, 0.70218 , 0.721544, 0.666886, 0.124931, 0.618286,
0.381086, 0.385643, 0.777175, 0.116089, 0.115487, 0.66351 ,
0.254884, 0.993888, 0.295434, 0.952523, 0.307047, 0.277261,
0.279101, 0.175724, 0.156383, 0.733165, 0.848142, 0.771184,
0.429492, 0.162176, 0.917064, 0.315044, 0.201473, 0.297038,
0.336647, 0.666109, 0.583888, 0.085031, 0.687006, 0.949655,
0.189912, 0.844027, 0.333288, 0.427035, 0.466369, 0.550659,
0.278213, 0.918769, 0.886555, 0.569488, 0.066379, 0.335751,
0.426863, 0.395746, 0.694221, 0.27276 , 0.503495, 0.067119,
0.038326, 0.599122, 0.947054, 0.671279, 0.434811, 0.509381,
0.749442, 0.058014, 0.482978, 0.466776, 0.357767, 0.949123,
0.41732 , 0.920461, 0.156433, 0.656662, 0.616418, 0.853428,
0.133295, 0.693007, 0.178449, 0.199526, 0.073224, 0.286515,
0.182026, 0.621523, 0.344584, 0.398556, 0.480369, 0.15335 ,
0.171846, 0.867082, 0.223855, 0.528301, 0.890192, 0.106352,
0.917886, 0.014855, 0.567682, 0.068854, 0.603535, 0.53205 ,
0.651362, 0.901225, 0.204337, 0.696081, 0.963924, 0.98139 ,
0.987911, 0.990947, 0.736021, 0.253574, 0.674722, 0.939368,
0.235419, 0.110521, 0.218023, 0.869778, 0.19683 , 0.958178,
0.972673, 0.745797, 0.445674, 0.470557, 0.549236, 0.335691,
0.884739, 0.918916, 0.441815, 0.116598, 0.359274, 0.814811,
0.387125, 0.982243, 0.78088 , 0.652565, 0.87003 , 0.604755,
0.255212, 0.730546, 0.493829, 0.257017, 0.833735, 0.070095,
0.52707 , 0.116163])
xMat.A[:,1].shape
(200,)
yMat
matrix([[3.176513],
[3.816464],
[4.550095],
[4.256571],
[4.560815],
[3.929515],
[3.52617 ],
[3.156393],
[3.110301],
[3.149813],
[3.476346],
[4.119688],
[4.282233],
[3.486582],
[4.655492],
[3.965162],
[3.5149 ],
[3.125947],
[4.094115],
[3.476039],
[3.21061 ],
[3.190612],
[4.631504],
[4.29589 ],
[3.085028],
[3.44808 ],
[3.16744 ],
[3.364266],
[3.993482],
[3.891471],
[3.143259],
[3.114204],
[3.851484],
[4.621899],
[4.580768],
[3.620992],
[3.580501],
[4.618706],
[3.676867],
[4.641845],
[3.175939],
[4.26498 ],
[3.558448],
[3.436632],
[3.831052],
[3.182853],
[3.498906],
[3.946833],
[3.900583],
[4.238522],
[4.23308 ],
[3.521557],
[3.203344],
[4.278105],
[3.555705],
[3.502661],
[3.859776],
[4.275956],
[3.916191],
[3.587961],
[3.183004],
[4.225236],
[4.231083],
[4.240544],
[3.222372],
[4.021445],
[3.567479],
[3.56258 ],
[4.262059],
[3.208813],
[3.169825],
[4.193949],
[3.491678],
[4.533306],
[3.550108],
[4.636427],
[3.557078],
[3.552874],
[3.494159],
[3.206828],
[3.195266],
[4.221292],
[4.413372],
[4.184347],
[3.742878],
[3.201878],
[4.648964],
[3.510117],
[3.274434],
[3.579622],
[3.489244],
[4.237386],
[3.913749],
[3.22899 ],
[4.286286],
[4.628614],
[3.239536],
[4.457997],
[3.513384],
[3.729674],
[3.834274],
[3.811155],
[3.598316],
[4.692514],
[4.604859],
[3.864912],
[3.184236],
[3.500796],
[3.743365],
[3.622905],
[4.310796],
[3.583357],
[3.901852],
[3.233521],
[3.105266],
[3.865544],
[4.628625],
[4.231213],
[3.791149],
[3.968271],
[4.25391 ],
[3.19471 ],
[3.996503],
[3.904358],
[3.503976],
[4.557545],
[3.699876],
[4.613614],
[3.140401],
[4.206717],
[3.969524],
[4.476096],
[3.136528],
[4.279071],
[3.200603],
[3.299012],
[3.209873],
[3.632942],
[3.248361],
[3.995783],
[3.563262],
[3.649712],
[3.951845],
[3.145031],
[3.181577],
[4.637087],
[3.404964],
[3.873188],
[4.633648],
[3.154768],
[4.623637],
[3.078132],
[3.913596],
[3.221817],
[3.938071],
[3.880822],
[4.176436],
[4.648161],
[3.332312],
[4.240614],
[4.532224],
[4.557105],
[4.610072],
[4.636569],
[4.229813],
[3.50086 ],
[4.245514],
[4.605182],
[3.45434 ],
[3.180775],
[3.38082 ],
[4.56502 ],
[3.279973],
[4.554241],
[4.63352 ],
[4.281037],
[3.844426],
[3.891601],
[3.849728],
[3.492215],
[4.592374],
[4.632025],
[3.75675 ],
[3.133555],
[3.567919],
[4.363382],
[3.560165],
[4.564305],
[4.215055],
[4.174999],
[4.58664 ],
[3.960008],
[3.529963],
[4.213412],
[3.908685],
[3.585821],
[4.374394],
[3.213817],
[3.952681],
[3.129283]])
'''
函数功能:数据集可视化
'''
def plotShow(dataSet):
xMat,yMat = get_Mat(dataSet)
plt.scatter(xMat.A[:,1],yMat.A,c='b',s=5)
plt.show()
plotShow(ex0)
4.5 计算回归系数
'''
函数功能:计算回归系数
参数说明:
dataSet:原始数据集
返回:
ws:回归系数
'''
def standRegres(dataSet):
xMat,yMat = get_Mat(dataSet)
xTx = xMat.T * xMat
if np.linalg.det(xTx) == 0:
print('矩阵为奇异矩阵,无法求逆!')
return
ws = xTx.I*(xMat.T*yMat) # xTx.I ,用来求逆矩阵
return ws
说明:det(A)指的是矩阵A的行列式(determinant),如果det(A)=0,则说明矩阵A是奇异矩阵,不可逆。
ws = standRegres(ex0)
ws
matrix([[3.00774324],
[1.69532264]])
4.6 绘制最佳拟合直线
'''
函数功能:绘制散点图和最佳拟合直线
'''
def plotReg(dataSet):
xMat,yMat = get_Mat(dataSet)
plt.scatter(xMat.A[:,1],yMat.A,c='b',s=5)
ws = standRegres(dataSet)
yHat = xMat*ws
plt.plot(xMat[:,1],yHat,c='r')
plt.xlabel("第2列特征的数值:xMat[:,1]")
plt.ylabel("预测值:yHat")
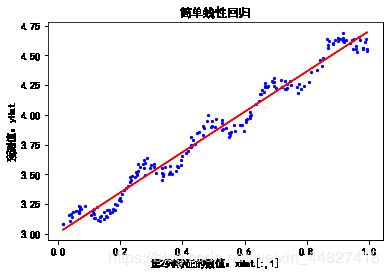
plt.title('简单线性回归')
plt.show()
# 绘制ex0数据集的散点图和最佳拟合直线
plotReg(ex0)
4.7 计算相关系数
xMat,yMat = get_Mat(ex0)
ws = standRegres(ex0)
yHat = xMat*ws
np.corrcoef(yHat.T,yMat.T) # 参数需要保证两个都是行向量
array([[1. , 0.98647356],
[0.98647356, 1. ]])
该矩阵包含所有两两组合的相关系数。可以看到,对角线上全部为1.0,因为自身匹配肯定是最完美的,而yHat和yMat的相关系数为0.98。看起来似乎是一个不错的结果。但是仔细观察数据集,会发现数据呈现有规律的波动,但是直线似乎没有很好的捕捉到这些波动。
局部加权线性回归
#此段代码供大家参考
xMat,yMat = get_Mat(ex0)
x=0.5
xi = np.arange(0,1.0,0.01)
k1,k2,k3=0.5,0.1,0.01
w1 = np.exp((xi-x)**2/(-2*k1**2))
w2 = np.exp((xi-x)**2/(-2*k2**2))
w3 = np.exp((xi-x)**2/(-2*k3**2))
#创建画布
fig = plt.figure(figsize=(6,8),dpi=100)
#子画布1,原始数据集
fig1 = fig.add_subplot(411)
plt.scatter(xMat.A[:,1],yMat.A,c='b',s=5)
#子画布2,k=0.5
fig2 = fig.add_subplot(412)
plt.plot(xi,w1,color='r')
plt.legend(['k = 0.5'])
#子画布3,k=0.1
fig3 = fig.add_subplot(413)
plt.plot(xi,w2,color='g')
plt.legend(['k = 0.1'])
#子画布4,k=0.01
fig4 = fig.add_subplot(414)
plt.plot(xi,w3,color='orange')
plt.legend(['k = 0.01'])
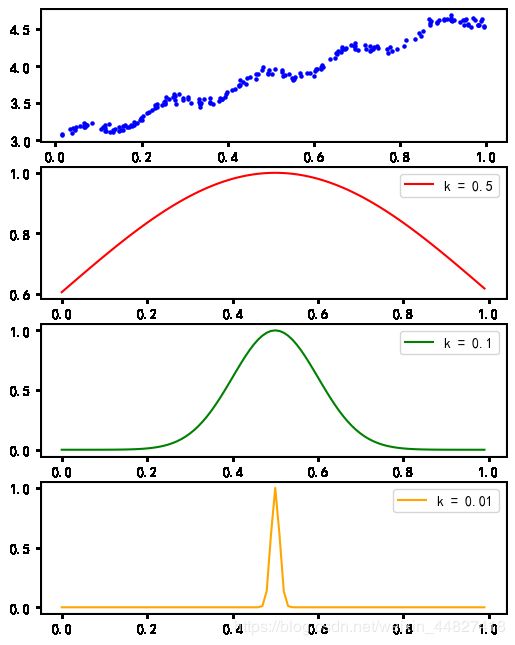
plt.show()
这里假定我们预测的点是x=0.5,最上面的图是原始数据集,从下面三张图可以看出随着k的减小,被用于训练模型的数据点越来越少。
1. 构建LWLR函数
这个过程与简单线性函数的基本一致,唯一不同的是加入了权重weights,这里我将权重参数求解和预测yHat放在了一个函数里面。
# np.eye(5) 单位矩阵
a_eye = np.eye(5)
a_eye[0,2]=55
a_eye
array([[ 1., 0., 55., 0., 0.],
[ 0., 1., 0., 0., 0.],
[ 0., 0., 1., 0., 0.],
[ 0., 0., 0., 1., 0.],
[ 0., 0., 0., 0., 1.]])
a_eye[0]
array([ 1., 0., 55., 0., 0.])
a_eye.T
array([[ 1., 0., 0., 0., 0.],
[ 0., 1., 0., 0., 0.],
[55., 0., 1., 0., 0.],
[ 0., 0., 0., 1., 0.],
[ 0., 0., 0., 0., 1.]])
a_eye.T[0]
array([1., 0., 0., 0., 0.])
'''
函数功能:计算局部加权线性回归的预测值
参数说明:
testMat:测试集
xMat:训练集的特征矩阵
yMat:训练集的标签矩阵
返回:
yHat:函数预测值
'''
def LWLR(testMat,xMat,yMat,k=1.0):
n = testMat.shape[0] # 测试数据集行数
m = xMat.shape[0] # 训练集特征矩阵行数
weights = np.mat(np.eye(m)) # 用单位矩阵来初始化权重矩阵,
yHat = np.zeros(n) # 用0矩阵来初始化预测值矩阵
for i in range(n):
for j in range(m):
diffMat = testMat[i] - xMat[j]
weights[j,j] = np.exp(diffMat*diffMat.T / (-2*k**2))
xTx = xMat.T*(weights*xMat)
if np.linalg.det(xTx) == 0:
print('矩阵为奇异矩阵,无法求逆')
return
ws = xTx.I*(xMat.T*(weights*yMat))
yHat[i] = testMat[i] * ws
return ws,yHat
xMat
matrix([[1. , 0.067732],
[1. , 0.42781 ],
[1. , 0.995731],
[1. , 0.738336],
[1. , 0.981083],
[1. , 0.526171],
[1. , 0.378887],
[1. , 0.033859],
[1. , 0.132791],
[1. , 0.138306],
[1. , 0.247809],
[1. , 0.64827 ],
[1. , 0.731209],
[1. , 0.236833],
[1. , 0.969788],
[1. , 0.607492],
[1. , 0.358622],
[1. , 0.147846],
[1. , 0.63782 ],
[1. , 0.230372],
[1. , 0.070237],
[1. , 0.067154],
[1. , 0.925577],
[1. , 0.717733],
[1. , 0.015371],
[1. , 0.33507 ],
[1. , 0.040486],
[1. , 0.212575],
[1. , 0.617218],
[1. , 0.541196],
[1. , 0.045353],
[1. , 0.126762],
[1. , 0.556486],
[1. , 0.901144],
[1. , 0.958476],
[1. , 0.274561],
[1. , 0.394396],
[1. , 0.87248 ],
[1. , 0.409932],
[1. , 0.908969],
[1. , 0.166819],
[1. , 0.665016],
[1. , 0.263727],
[1. , 0.231214],
[1. , 0.552928],
[1. , 0.047744],
[1. , 0.365746],
[1. , 0.495002],
[1. , 0.493466],
[1. , 0.792101],
[1. , 0.76966 ],
[1. , 0.251821],
[1. , 0.181951],
[1. , 0.808177],
[1. , 0.334116],
[1. , 0.33863 ],
[1. , 0.452584],
[1. , 0.69477 ],
[1. , 0.590902],
[1. , 0.307928],
[1. , 0.148364],
[1. , 0.70218 ],
[1. , 0.721544],
[1. , 0.666886],
[1. , 0.124931],
[1. , 0.618286],
[1. , 0.381086],
[1. , 0.385643],
[1. , 0.777175],
[1. , 0.116089],
[1. , 0.115487],
[1. , 0.66351 ],
[1. , 0.254884],
[1. , 0.993888],
[1. , 0.295434],
[1. , 0.952523],
[1. , 0.307047],
[1. , 0.277261],
[1. , 0.279101],
[1. , 0.175724],
[1. , 0.156383],
[1. , 0.733165],
[1. , 0.848142],
[1. , 0.771184],
[1. , 0.429492],
[1. , 0.162176],
[1. , 0.917064],
[1. , 0.315044],
[1. , 0.201473],
[1. , 0.297038],
[1. , 0.336647],
[1. , 0.666109],
[1. , 0.583888],
[1. , 0.085031],
[1. , 0.687006],
[1. , 0.949655],
[1. , 0.189912],
[1. , 0.844027],
[1. , 0.333288],
[1. , 0.427035],
[1. , 0.466369],
[1. , 0.550659],
[1. , 0.278213],
[1. , 0.918769],
[1. , 0.886555],
[1. , 0.569488],
[1. , 0.066379],
[1. , 0.335751],
[1. , 0.426863],
[1. , 0.395746],
[1. , 0.694221],
[1. , 0.27276 ],
[1. , 0.503495],
[1. , 0.067119],
[1. , 0.038326],
[1. , 0.599122],
[1. , 0.947054],
[1. , 0.671279],
[1. , 0.434811],
[1. , 0.509381],
[1. , 0.749442],
[1. , 0.058014],
[1. , 0.482978],
[1. , 0.466776],
[1. , 0.357767],
[1. , 0.949123],
[1. , 0.41732 ],
[1. , 0.920461],
[1. , 0.156433],
[1. , 0.656662],
[1. , 0.616418],
[1. , 0.853428],
[1. , 0.133295],
[1. , 0.693007],
[1. , 0.178449],
[1. , 0.199526],
[1. , 0.073224],
[1. , 0.286515],
[1. , 0.182026],
[1. , 0.621523],
[1. , 0.344584],
[1. , 0.398556],
[1. , 0.480369],
[1. , 0.15335 ],
[1. , 0.171846],
[1. , 0.867082],
[1. , 0.223855],
[1. , 0.528301],
[1. , 0.890192],
[1. , 0.106352],
[1. , 0.917886],
[1. , 0.014855],
[1. , 0.567682],
[1. , 0.068854],
[1. , 0.603535],
[1. , 0.53205 ],
[1. , 0.651362],
[1. , 0.901225],
[1. , 0.204337],
[1. , 0.696081],
[1. , 0.963924],
[1. , 0.98139 ],
[1. , 0.987911],
[1. , 0.990947],
[1. , 0.736021],
[1. , 0.253574],
[1. , 0.674722],
[1. , 0.939368],
[1. , 0.235419],
[1. , 0.110521],
[1. , 0.218023],
[1. , 0.869778],
[1. , 0.19683 ],
[1. , 0.958178],
[1. , 0.972673],
[1. , 0.745797],
[1. , 0.445674],
[1. , 0.470557],
[1. , 0.549236],
[1. , 0.335691],
[1. , 0.884739],
[1. , 0.918916],
[1. , 0.441815],
[1. , 0.116598],
[1. , 0.359274],
[1. , 0.814811],
[1. , 0.387125],
[1. , 0.982243],
[1. , 0.78088 ],
[1. , 0.652565],
[1. , 0.87003 ],
[1. , 0.604755],
[1. , 0.255212],
[1. , 0.730546],
[1. , 0.493829],
[1. , 0.257017],
[1. , 0.833735],
[1. , 0.070095],
[1. , 0.52707 ],
[1. , 0.116163]])
xMat[0]
matrix([[1. , 0.067732]])
xMat[0] - xMat[1]
matrix([[ 0. , -0.360078]])
2. 不同k值的结果图
我们调整k值,然后查看不同k值对模型的影响
xMat,yMat = get_Mat(ex0)
#将数据点排列(argsort()默认升序排列,返回索引)
srtInd = xMat[:,1].argsort(0)
srtInd
matrix([[151],
[ 24],
[ 7],
[114],
[ 26],
[ 30],
[ 45],
[121],
[106],
[113],
[ 21],
[ 0],
[153],
[197],
[ 20],
[136],
[ 93],
[149],
[169],
[ 70],
[ 69],
[199],
[183],
[ 64],
[ 31],
[ 8],
[132],
[ 9],
[ 17],
[ 60],
[143],
[ 80],
[128],
[ 85],
[ 40],
[144],
[ 79],
[134],
[ 52],
[138],
[ 96],
[172],
[135],
[ 88],
[158],
[ 27],
[170],
[146],
[ 19],
[ 43],
[168],
[ 13],
[ 10],
[ 51],
[165],
[ 72],
[192],
[195],
[ 42],
[111],
[ 35],
[ 77],
[102],
[ 78],
[137],
[ 74],
[ 89],
[ 76],
[ 59],
[ 87],
[ 98],
[ 54],
[ 25],
[179],
[107],
[ 90],
[ 55],
[140],
[124],
[ 16],
[184],
[ 46],
[ 6],
[ 66],
[ 67],
[186],
[ 36],
[109],
[141],
[ 38],
[126],
[108],
[ 99],
[ 1],
[ 84],
[118],
[182],
[176],
[ 56],
[100],
[123],
[177],
[142],
[122],
[ 48],
[194],
[ 47],
[112],
[119],
[ 5],
[198],
[147],
[155],
[ 29],
[178],
[101],
[ 44],
[ 32],
[152],
[105],
[ 92],
[ 58],
[115],
[154],
[191],
[ 15],
[130],
[ 28],
[ 65],
[139],
[ 18],
[ 11],
[156],
[189],
[129],
[ 71],
[ 41],
[ 91],
[ 63],
[117],
[166],
[ 94],
[133],
[110],
[ 57],
[159],
[ 61],
[ 23],
[ 62],
[193],
[ 12],
[ 81],
[164],
[ 3],
[175],
[120],
[ 50],
[ 83],
[ 68],
[188],
[ 49],
[ 53],
[185],
[196],
[ 97],
[ 82],
[131],
[145],
[171],
[190],
[ 37],
[180],
[104],
[148],
[ 33],
[157],
[ 39],
[ 86],
[150],
[103],
[181],
[127],
[ 22],
[167],
[116],
[125],
[ 95],
[ 75],
[173],
[ 34],
[160],
[ 14],
[174],
[ 4],
[161],
[187],
[162],
[163],
[ 73],
[ 2]], dtype=int64)
xMat[srtInd]
matrix([[[1. , 0.014855]],
[[1. , 0.015371]],
[[1. , 0.033859]],
[[1. , 0.038326]],
[[1. , 0.040486]],
[[1. , 0.045353]],
[[1. , 0.047744]],
[[1. , 0.058014]],
[[1. , 0.066379]],
[[1. , 0.067119]],
[[1. , 0.067154]],
[[1. , 0.067732]],
[[1. , 0.068854]],
[[1. , 0.070095]],
[[1. , 0.070237]],
[[1. , 0.073224]],
[[1. , 0.085031]],
[[1. , 0.106352]],
[[1. , 0.110521]],
[[1. , 0.115487]],
[[1. , 0.116089]],
[[1. , 0.116163]],
[[1. , 0.116598]],
[[1. , 0.124931]],
[[1. , 0.126762]],
[[1. , 0.132791]],
[[1. , 0.133295]],
[[1. , 0.138306]],
[[1. , 0.147846]],
[[1. , 0.148364]],
[[1. , 0.15335 ]],
[[1. , 0.156383]],
[[1. , 0.156433]],
[[1. , 0.162176]],
[[1. , 0.166819]],
[[1. , 0.171846]],
[[1. , 0.175724]],
[[1. , 0.178449]],
[[1. , 0.181951]],
[[1. , 0.182026]],
[[1. , 0.189912]],
[[1. , 0.19683 ]],
[[1. , 0.199526]],
[[1. , 0.201473]],
[[1. , 0.204337]],
[[1. , 0.212575]],
[[1. , 0.218023]],
[[1. , 0.223855]],
[[1. , 0.230372]],
[[1. , 0.231214]],
[[1. , 0.235419]],
[[1. , 0.236833]],
[[1. , 0.247809]],
[[1. , 0.251821]],
[[1. , 0.253574]],
[[1. , 0.254884]],
[[1. , 0.255212]],
[[1. , 0.257017]],
[[1. , 0.263727]],
[[1. , 0.27276 ]],
[[1. , 0.274561]],
[[1. , 0.277261]],
[[1. , 0.278213]],
[[1. , 0.279101]],
[[1. , 0.286515]],
[[1. , 0.295434]],
[[1. , 0.297038]],
[[1. , 0.307047]],
[[1. , 0.307928]],
[[1. , 0.315044]],
[[1. , 0.333288]],
[[1. , 0.334116]],
[[1. , 0.33507 ]],
[[1. , 0.335691]],
[[1. , 0.335751]],
[[1. , 0.336647]],
[[1. , 0.33863 ]],
[[1. , 0.344584]],
[[1. , 0.357767]],
[[1. , 0.358622]],
[[1. , 0.359274]],
[[1. , 0.365746]],
[[1. , 0.378887]],
[[1. , 0.381086]],
[[1. , 0.385643]],
[[1. , 0.387125]],
[[1. , 0.394396]],
[[1. , 0.395746]],
[[1. , 0.398556]],
[[1. , 0.409932]],
[[1. , 0.41732 ]],
[[1. , 0.426863]],
[[1. , 0.427035]],
[[1. , 0.42781 ]],
[[1. , 0.429492]],
[[1. , 0.434811]],
[[1. , 0.441815]],
[[1. , 0.445674]],
[[1. , 0.452584]],
[[1. , 0.466369]],
[[1. , 0.466776]],
[[1. , 0.470557]],
[[1. , 0.480369]],
[[1. , 0.482978]],
[[1. , 0.493466]],
[[1. , 0.493829]],
[[1. , 0.495002]],
[[1. , 0.503495]],
[[1. , 0.509381]],
[[1. , 0.526171]],
[[1. , 0.52707 ]],
[[1. , 0.528301]],
[[1. , 0.53205 ]],
[[1. , 0.541196]],
[[1. , 0.549236]],
[[1. , 0.550659]],
[[1. , 0.552928]],
[[1. , 0.556486]],
[[1. , 0.567682]],
[[1. , 0.569488]],
[[1. , 0.583888]],
[[1. , 0.590902]],
[[1. , 0.599122]],
[[1. , 0.603535]],
[[1. , 0.604755]],
[[1. , 0.607492]],
[[1. , 0.616418]],
[[1. , 0.617218]],
[[1. , 0.618286]],
[[1. , 0.621523]],
[[1. , 0.63782 ]],
[[1. , 0.64827 ]],
[[1. , 0.651362]],
[[1. , 0.652565]],
[[1. , 0.656662]],
[[1. , 0.66351 ]],
[[1. , 0.665016]],
[[1. , 0.666109]],
[[1. , 0.666886]],
[[1. , 0.671279]],
[[1. , 0.674722]],
[[1. , 0.687006]],
[[1. , 0.693007]],
[[1. , 0.694221]],
[[1. , 0.69477 ]],
[[1. , 0.696081]],
[[1. , 0.70218 ]],
[[1. , 0.717733]],
[[1. , 0.721544]],
[[1. , 0.730546]],
[[1. , 0.731209]],
[[1. , 0.733165]],
[[1. , 0.736021]],
[[1. , 0.738336]],
[[1. , 0.745797]],
[[1. , 0.749442]],
[[1. , 0.76966 ]],
[[1. , 0.771184]],
[[1. , 0.777175]],
[[1. , 0.78088 ]],
[[1. , 0.792101]],
[[1. , 0.808177]],
[[1. , 0.814811]],
[[1. , 0.833735]],
[[1. , 0.844027]],
[[1. , 0.848142]],
[[1. , 0.853428]],
[[1. , 0.867082]],
[[1. , 0.869778]],
[[1. , 0.87003 ]],
[[1. , 0.87248 ]],
[[1. , 0.884739]],
[[1. , 0.886555]],
[[1. , 0.890192]],
[[1. , 0.901144]],
[[1. , 0.901225]],
[[1. , 0.908969]],
[[1. , 0.917064]],
[[1. , 0.917886]],
[[1. , 0.918769]],
[[1. , 0.918916]],
[[1. , 0.920461]],
[[1. , 0.925577]],
[[1. , 0.939368]],
[[1. , 0.947054]],
[[1. , 0.949123]],
[[1. , 0.949655]],
[[1. , 0.952523]],
[[1. , 0.958178]],
[[1. , 0.958476]],
[[1. , 0.963924]],
[[1. , 0.969788]],
[[1. , 0.972673]],
[[1. , 0.981083]],
[[1. , 0.98139 ]],
[[1. , 0.982243]],
[[1. , 0.987911]],
[[1. , 0.990947]],
[[1. , 0.993888]],
[[1. , 0.995731]]])
xSort=xMat[srtInd][:,0]
xSort
matrix([[1. , 0.014855],
[1. , 0.015371],
[1. , 0.033859],
[1. , 0.038326],
[1. , 0.040486],
[1. , 0.045353],
[1. , 0.047744],
[1. , 0.058014],
[1. , 0.066379],
[1. , 0.067119],
[1. , 0.067154],
[1. , 0.067732],
[1. , 0.068854],
[1. , 0.070095],
[1. , 0.070237],
[1. , 0.073224],
[1. , 0.085031],
[1. , 0.106352],
[1. , 0.110521],
[1. , 0.115487],
[1. , 0.116089],
[1. , 0.116163],
[1. , 0.116598],
[1. , 0.124931],
[1. , 0.126762],
[1. , 0.132791],
[1. , 0.133295],
[1. , 0.138306],
[1. , 0.147846],
[1. , 0.148364],
[1. , 0.15335 ],
[1. , 0.156383],
[1. , 0.156433],
[1. , 0.162176],
[1. , 0.166819],
[1. , 0.171846],
[1. , 0.175724],
[1. , 0.178449],
[1. , 0.181951],
[1. , 0.182026],
[1. , 0.189912],
[1. , 0.19683 ],
[1. , 0.199526],
[1. , 0.201473],
[1. , 0.204337],
[1. , 0.212575],
[1. , 0.218023],
[1. , 0.223855],
[1. , 0.230372],
[1. , 0.231214],
[1. , 0.235419],
[1. , 0.236833],
[1. , 0.247809],
[1. , 0.251821],
[1. , 0.253574],
[1. , 0.254884],
[1. , 0.255212],
[1. , 0.257017],
[1. , 0.263727],
[1. , 0.27276 ],
[1. , 0.274561],
[1. , 0.277261],
[1. , 0.278213],
[1. , 0.279101],
[1. , 0.286515],
[1. , 0.295434],
[1. , 0.297038],
[1. , 0.307047],
[1. , 0.307928],
[1. , 0.315044],
[1. , 0.333288],
[1. , 0.334116],
[1. , 0.33507 ],
[1. , 0.335691],
[1. , 0.335751],
[1. , 0.336647],
[1. , 0.33863 ],
[1. , 0.344584],
[1. , 0.357767],
[1. , 0.358622],
[1. , 0.359274],
[1. , 0.365746],
[1. , 0.378887],
[1. , 0.381086],
[1. , 0.385643],
[1. , 0.387125],
[1. , 0.394396],
[1. , 0.395746],
[1. , 0.398556],
[1. , 0.409932],
[1. , 0.41732 ],
[1. , 0.426863],
[1. , 0.427035],
[1. , 0.42781 ],
[1. , 0.429492],
[1. , 0.434811],
[1. , 0.441815],
[1. , 0.445674],
[1. , 0.452584],
[1. , 0.466369],
[1. , 0.466776],
[1. , 0.470557],
[1. , 0.480369],
[1. , 0.482978],
[1. , 0.493466],
[1. , 0.493829],
[1. , 0.495002],
[1. , 0.503495],
[1. , 0.509381],
[1. , 0.526171],
[1. , 0.52707 ],
[1. , 0.528301],
[1. , 0.53205 ],
[1. , 0.541196],
[1. , 0.549236],
[1. , 0.550659],
[1. , 0.552928],
[1. , 0.556486],
[1. , 0.567682],
[1. , 0.569488],
[1. , 0.583888],
[1. , 0.590902],
[1. , 0.599122],
[1. , 0.603535],
[1. , 0.604755],
[1. , 0.607492],
[1. , 0.616418],
[1. , 0.617218],
[1. , 0.618286],
[1. , 0.621523],
[1. , 0.63782 ],
[1. , 0.64827 ],
[1. , 0.651362],
[1. , 0.652565],
[1. , 0.656662],
[1. , 0.66351 ],
[1. , 0.665016],
[1. , 0.666109],
[1. , 0.666886],
[1. , 0.671279],
[1. , 0.674722],
[1. , 0.687006],
[1. , 0.693007],
[1. , 0.694221],
[1. , 0.69477 ],
[1. , 0.696081],
[1. , 0.70218 ],
[1. , 0.717733],
[1. , 0.721544],
[1. , 0.730546],
[1. , 0.731209],
[1. , 0.733165],
[1. , 0.736021],
[1. , 0.738336],
[1. , 0.745797],
[1. , 0.749442],
[1. , 0.76966 ],
[1. , 0.771184],
[1. , 0.777175],
[1. , 0.78088 ],
[1. , 0.792101],
[1. , 0.808177],
[1. , 0.814811],
[1. , 0.833735],
[1. , 0.844027],
[1. , 0.848142],
[1. , 0.853428],
[1. , 0.867082],
[1. , 0.869778],
[1. , 0.87003 ],
[1. , 0.87248 ],
[1. , 0.884739],
[1. , 0.886555],
[1. , 0.890192],
[1. , 0.901144],
[1. , 0.901225],
[1. , 0.908969],
[1. , 0.917064],
[1. , 0.917886],
[1. , 0.918769],
[1. , 0.918916],
[1. , 0.920461],
[1. , 0.925577],
[1. , 0.939368],
[1. , 0.947054],
[1. , 0.949123],
[1. , 0.949655],
[1. , 0.952523],
[1. , 0.958178],
[1. , 0.958476],
[1. , 0.963924],
[1. , 0.969788],
[1. , 0.972673],
[1. , 0.981083],
[1. , 0.98139 ],
[1. , 0.982243],
[1. , 0.987911],
[1. , 0.990947],
[1. , 0.993888],
[1. , 0.995731]])
#计算不同k取值下的y估计值yHat
ws1,yHat1 = LWLR(xMat,xMat,yMat,k=1.0)
ws2,yHat2 = LWLR(xMat,xMat,yMat,k=0.01)
ws3,yHat3 = LWLR(xMat,xMat,yMat,k=0.003)
#创建画布
fig = plt.figure(figsize=(6,8),dpi=100)
#子图1绘制k=1.0的曲线
fig1=fig.add_subplot(311)
plt.scatter(xMat[:,1].A,yMat.A,c='b',s=2)
plt.plot(xSort[:,1],yHat1[srtInd],linewidth=1,color='r')
plt.title('局部加权回归曲线,k=1.0',size=10,color='r')
#子图2绘制k=0.01的曲线
fig2=fig.add_subplot(312)
plt.scatter(xMat[:,1].A,yMat.A,c='b',s=2)
plt.plot(xSort[:,1],yHat2[srtInd],linewidth=1,color='r')
plt.title('局部加权回归曲线,k=0.01',size=10,color='r')
#子图3绘制k=0.003的曲线
fig3=fig.add_subplot(313)
plt.scatter(xMat[:,1].A,yMat.A,c='b',s=2)
plt.plot(xSort[:,1],yHat3[srtInd],linewidth=1,color='r')
plt.title('局部加权回归曲线,k=0.003',size=10,color='r')
#调整子图的间距
plt.tight_layout(pad=1.2)
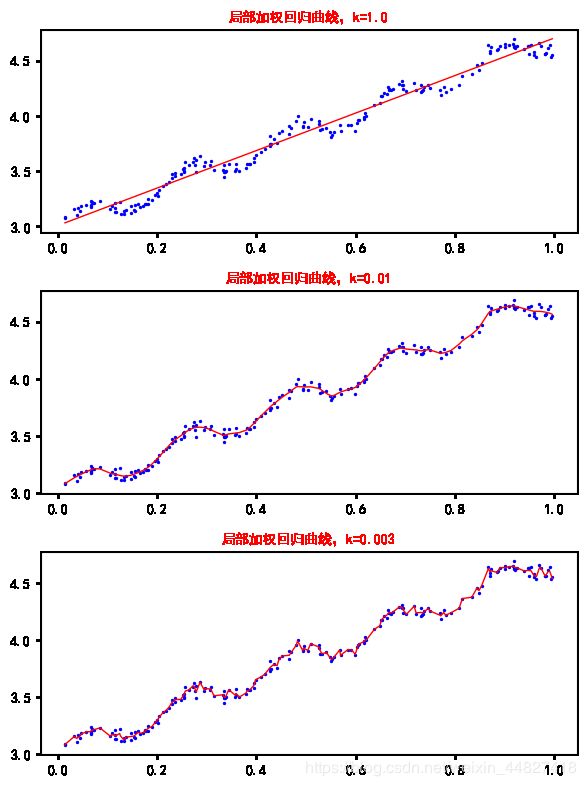
plt.show()
这三个图是不同平滑值绘出的局部加权线性回归结果。当k=1.0时,模型的效果与最小二乘法差不多;k=0.01时,该模型基本上已经挖出了数据的潜在规律,当继续减小到k=0.003时,会发现模型考虑了太多的噪音,进而导致了过拟合现象。
#四种模型相关系数比较
np.corrcoef(yHat.T,yMat.T) # 最小二乘法
array([[1. , 0.98647356],
[0.98647356, 1. ]])
np.corrcoef(yHat1,yMat.T) # k=1.0模型
array([[1. , 0.98647703],
[0.98647703, 1. ]])
np.corrcoef(yHat2,yMat.T) # k=0.01模型
array([[1. , 0.9985249],
[0.9985249, 1. ]])
np.corrcoef(yHat3,yMat.T) # k=0.003模型
array([[1. , 0.99931945],
[0.99931945, 1. ]])
局部加权线性回归也存在一个问题——增加了计算量,因为它对每个点预测都要使用整个数据集。从不同k值的结果图中可以看出,当k=0.01时模型可以很好地拟合数据潜在规律,但是同时看一下,k值与权重关系图,可以发现,当k=0.01时,大部分数据点的权重都接近0,也就是说他们基本上可以不用带入计算。所以如果一开始就能去掉这些数据点的计算,那么就可以大大减少程序的运行时间了,从而缓解计算量增加带来的问题。后面我们会讲解这个操作。