python数据可视化之Seaborn(三):分布可视化
写在开头:今天开始分享一下seaborn对于数据集分布的设计。该文章主要借鉴seaborn文档,会附在结尾链接。
前文回顾:
第一节分享了Seaborn绘图的整体颜色与风格比例调控,可点击链接查看。
python数据可视化之Seaborn(一)
第二节分享了连续、分类、离散数据的绘图颜色的方法,可点击链接查看。
python数据可视化之Seaborn(二)
Seaborn可视化内容安排
在Seaborn的学习中安排如下,
一、画风设置:会简单介绍一下绘图风格(一)与颜色风格(二)的设置;
二、绘图技巧:这里会介绍数据集(三)、相关数据(四)、分类数据(五)、线性关系(六)可视化的相关内容;
三、结构网络:本节主要介绍数据识别结构网络的绘图(七)。
二、Seaborn绘图技巧
数据集分布可视化
当我们处理数据集数据的时候,我们往往需要查看数据的分布情况,判断其属于哪种分布,或者判断其是否正态, 因为在有些统计模型下需要正态的假定,本章我们就会对单变量数据的分布直方图、核密度图,双变量分布矩阵图进行和一些个性化设置进行分享。
绘制单变量分布
在绘制图之前我们先载入本章需要的包,
import numpy as np
import pandas as pd
from scipy import stats, integrate
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
np.random.seed(42)
直方图
在seaborn中,对于单变量数据分布方法观察最便捷的方式就是绘制直方图和核密度估计,使用的就是distplot()函数,直方图其实就是根据数据的大小,将数据分成一段一段的矩形,来观察数据的分布情况。
sns.set_style("darkgrid")
x = np.random.normal(size=200)
sns.distplot(x, color='y')
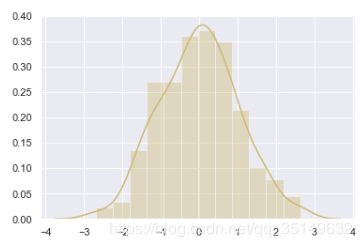
我们可以移除核密度估计线,在轴上加上垂直小标签来表示数据所在的位置,同样还可以调整矩阵的数量,来对图像进行重新绘制,
sns.distplot(x, kde=False, rug=True, bins=20)
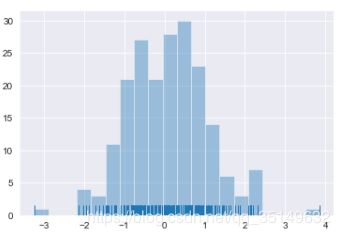
绘制直方图可以粗略的观察到数据的分布情况,但直方图存在比较大的缺陷就是其边界问题,直方图的边界过于强硬,将数据按照固定的不能移动的距离进行分类,使得图形包容性不够强。为此引入了核密度分析,核密度函数图引入了核函数,使得边界变得灵活。
核密度估计
核密度估计能够将直方图的信息更加全面的包括进来,绘制出更加光滑的曲线,同样可以通过distplot()函数表示,
sns.distplot(x, hist=False, rug=True, color='g')

当然除了distplot()可以绘制核密度函数图,还可以单独使用kdeplot()绘制核密度,核密度估计最重要的两个参数一个是核函数的选择,另一个是窗宽的选择,窗宽的选择类似于直方图矩形的宽长度的选择,核函数的选择也就是记录一个窗宽里数量的方法,一般是添加距离中心的数会赋予更大的权重,远离中心赋予更小的权重。但最重要的还是窗宽的选择,一般软件会自动选择最优窗宽,下面给大家进行展示,
sns.kdeplot(x)
sns.kdeplot(x, bw=.25, label="bw:0.25")
sns.kdeplot(x, bw=3, label="bw:3")
plt.legend()
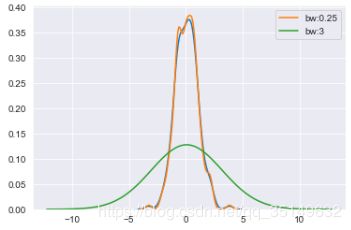
从上图可以看到,自动选择曲线和0.25窗宽的曲线相近,说明自动选择的窗宽可能近似于0.25。当然因为上述的绘图包含了全部的信息,为了删去左右较远的信息,可以调节cut参数进行调节。
sns.kdeplot(x, shade=True, cut=0, color='y')
sns.rugplot(x, color='y')

数据分布拟合
我们还能够通过distplot()函数对数据分布进行拟合绘制出一条光滑曲线,
x = np.random.gamma(7, size=200)
sns.distplot(x, kde=False, fit=stats.gamma)

绘制双变量分布
有时候双变量分布的可视化也是比较重要的,比如为了观察人群身体形态分布,身高体重二维变量就能够很好的反映出一个综合的情况,在seaborn中绘图可以使用jointplot()进行绘图,首先我们把数据进行模拟生成,根据经验我们设置一下身高和体重的模拟数据。可以利用jointplot()绘制出一个二维的散点图。
二维散点图
#设置均值与协方差矩阵
mean, cov = [1.7, 130], [(1, .65),(.65, 1)]
data = np.random.multivariate_normal(mean, cov, 200)
#生成结构化格式
df = pd.DataFrame(data, columns=["x", "y"])
sns.jointplot(x='x', y='y', data=df)

Hexbin绘图
hexbin图是直方图的双变量类型的变种,用六边形的颜色来表示在该区域观测量的大小,可以利用jointplot()内置参数进行绘制,
with sns.axes_style("white"):
sns.jointplot(x=x, y=y, kind="hex", color="r")
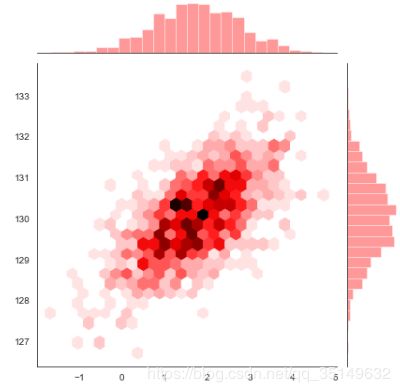
核密度估计
除了hexbin和散点图来绘制二元分布的方法外,还可以通过核密度估计来进行双变量的可视化,使用的是多元核密度估计的方法,该方法与单变量的核密度估计差别不大。
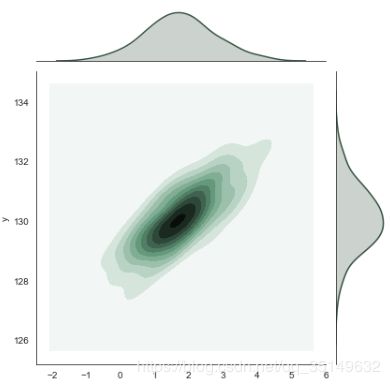
同样也可以使用kdeplot()函数来绘制二维核密度图形,
f, ax= plt.subplots(figsize=(7, 7))
sns.kdeplot(df.x, df.y, ax=ax)
sns.rugplot(df.x, color="g", ax=ax)
sns.rugplot(df.y, vertical=True, ax=ax)

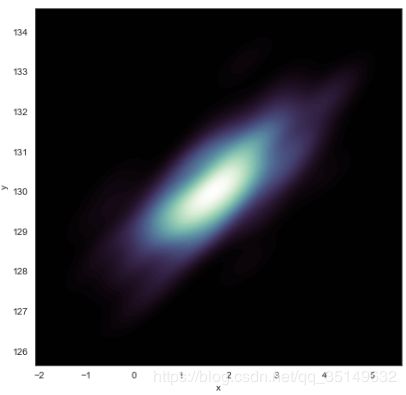
为了使得图形更加的光滑,可以改变n_levels参数的值使得出现更多的圈,来使得图像柔和,
f, ax = plt.subplots(figsize=(7, 7))
cmap = sns.cubehelix_palette(start=.5, rot=-.6, as_cmap=True, dark=0, light=1, reverse=True)
ax = sns.kdeplot(df.x, df.y, cmap=cmap, n_levels=100, shade=True)
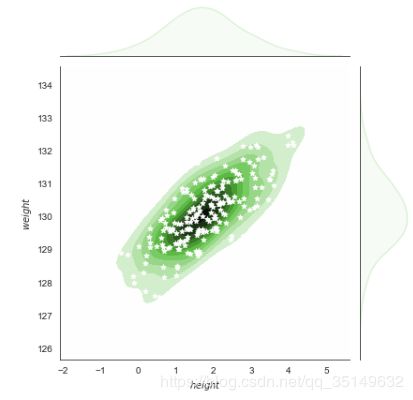
对于jointplot的个性化绘图,还可以添加更多图层来调整可视化,使用的方法是JointGrid()里面添加图层的方法,
plt.figure(figsize=(7,7))
sns.set_palette(sns.color_palette("GnBu"))
g = sns.jointplot(x="x", y="y", data=df, kind="kde")
g.plot_joint(plt.scatter, c="w", s=30, linewiDth=1, marker="*")
#这里的collections[0].set_alpha(0.1)是设置添加背景图层的透明图,具体不是很明白
g.ax_joint.collections[0].set_alpha(0.1)
g.set_axis_labels("$height$","$weight$")
可视化分布矩阵
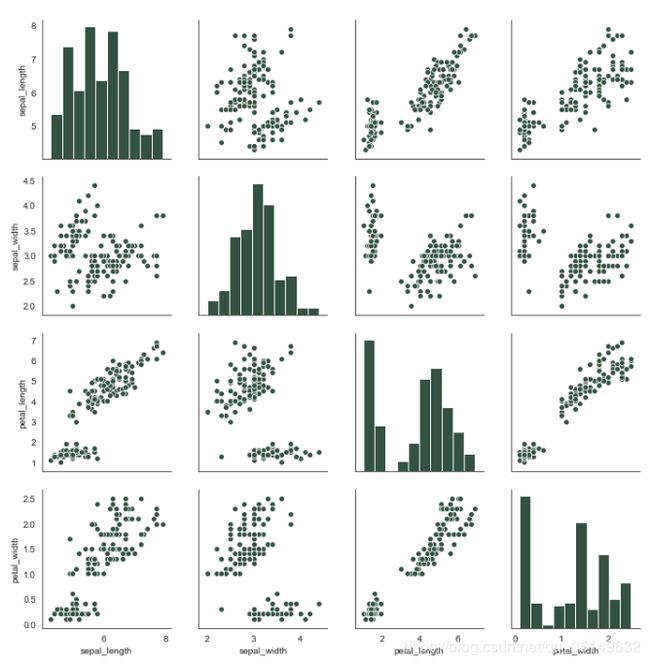
可视化分布矩阵,就有一点像相关可视化矩阵一样,就是横纵分别为多个变量,然后图像表示两两之间的关系,这种图适合在变量不是很多的时候使用,
sns.set_palette(sns.color_palette("BuGn_d"))
iris = sns.load_dataset("iris")
sns.pairplot(iris)
joinplot()有joinGrid()函数,同样pairplot()函数有PairGrid()一样,
sns.set_palette(sns.color_palette("RdPu"))
g = sns.PairGrid(iris, hue="species")
g = g.map_diag(plt.hist)
g = g.map_offdiag(plt.scatter)
g = g.add_legend()

结语
本节讲述了如何去展示数据的分布可视化,这是了解数据分布的第一步,后文会进一步展示面对不同数据的情况下,可以绘制哪些图形。
谢谢阅读。
参考
Seaborn可视化文档
Seaborn函数文档