Interpretable Machine Learning中GLM,GAM等
关于GLM,GAM等的描述
线性回归模型的最大优势也是最大的弱点是预测被建模为特征的加权和。此外,线性模型还有许多其他假设。所有这些假设在实际中经常被违反的坏消息是给定特征的结果可能具有非高斯分布,特征可能相互作用,特征与结果之间的关系可能是非线性的。好消息是,统计界已经开发了各种修改,将线性回归模型从简单的刀片转换为瑞士刀。
如广义线性模型(GLM)和广义加法模型(GAM)可扩展线性模型。
让记住线性回归模型的公式:
![]()
线性回归模型假设实例的结果y可以通过其p特征的加权和以及遵循高斯分布的单个误差ε来表示。 通过将数据强制转换为公式的紧身胸衣,我们获得了大量的模型可解释性。 特征效应是相加的,意味着没有相互作用,并且关系是线性的,意味着特征的增加可以直接转化为预测结果的增加/减少。 线性模型允许我们将特征和预期结果之间的关系压缩为单个数字,即估计的权重。
但是,对于许多现实世界的预测问题,简单的加权和过于严格。 在本章中,我们将了解经典线性回归模型的三个问题以及如何解决它们。 可能违反假设的问题还有很多,但我们将重点关注以下三个问题:
问题1:给定特征的目标结果y不遵循高斯分布。
示例:假设我想预测在给定的一天骑自行车的时间。作为特征我有一天的类型,天气等。如果我使用线性模型,它可以预测负分钟,因为它假定高斯分布不会在0分钟停止。此外,如果我想用线性模型预测概率,我可以得到负数或大于1的概率。
解决方案:广义线性模型(GLM)。
问题2:这些特征相互影响。
示例:平均而言,小雨对我骑车的欲望有轻微的负面影响。但是在夏天,在高峰时段,我欢迎下雨,因为那时所有的天气晴朗的骑车人都呆在家里,我自己也有自行车道!这是时间和天气之间的相互作用,纯粹的加性模型无法捕捉。
解决方案:手动添加交互。
问题3:特征与y之间的真实关系不是线性的。
示例:在0到25摄氏度之间,温度对我骑自行车的愿望的影响可以是线性的,这意味着从0到1度的增加导致循环期望的增加从20增加到21。但是在更高的温度下,我的动力是循环水平甚至减少 - 我不喜欢在太热的时候骑自行车。
解决方案:广义附加模型(GAM);特征转换。
非高斯结果 - GLM
线性回归模型假设给定输入特征的结果遵循高斯分布。这个假设排除了许多情况:结果也可以是一个类别(癌症与健康),计数(儿童数量),事件发生的时间(机器故障的时间)或非常倾斜的结果一些非常高的值(家庭收入)。线性回归模型可以扩展到对所有这些类型的结果进行建模。此扩展名称为广义线性模型或简称GLM。在本章中,我将使用名称GLM来表示通用框架和该框架中的特定模型。任何GLM的核心概念是:保持特征的加权和,但允许非高斯结果分布,并通过可能的非线性函数连接该分布的预期均值和加权和。例如,逻辑回归模型假定结果的伯努利分布,并使用逻辑函数链接预期均值和加权和。
GLM使用链接函数g在数学上将特征的加权和与假定分布的平均值相关联,其可以根据结果的类型灵活地选择。
![]()
GLM由三个部分组成:链接函数g,加权和XTβ(有时称为线性预测器)和来自指定EY的指数族的概率分布。
指数族(The exponential family)是一组分布,可以使用相同(参数化)公式编写,该公式包括指数,分布的均值和方差以及一些其他参数。我不会进入数学细节,因为这是一个我不想进入的非常大的宇宙。维基百科有一个来自指数家族的整齐分布列表。可以为您的GLM选择此列表中的任何分发。根据您要预测的结果类型,选择合适的分布。结果是否属于某事(例如,住在一个家庭中的儿童人数)?那么泊松分布可能是一个不错的选择。结果总是积极的(例如两次事件之间的时间)?那么指数分布可能是一个不错的选择。
让我们将经典线性模型视为GLM的一个特例。经典线性模型中高斯分布的链接函数只是标识函数。高斯分布由均值和方差参数参数化。平均值描述了我们平均预期的值,方差描述了这个值围绕该平均值变化的程度。在线性模型中,链接函数将特征的加权和与高斯分布的均值相关联。
在GLM框架下,这个概念推广到任何分布(来自指数族)和任意链接函数。如果y是某事物的数量,例如某人在某一天饮用的咖啡数量,我们可以使用具有Poisson分布的GLM和自然对数作为链接函数对其进行建模:
![]()
逻辑回归模型也是GLM,它假定伯努利分布并使用逻辑函数作为链接函数。 逻辑回归中使用的二项分布的均值是y为1的概率。
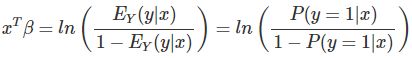
如果我们解决这个方程将P(y = 1)放在一边,我们得到逻辑回归公式:

来自指数族的每个分布都具有规范链接函数,该函数可以从分布中以数学方式导出。 GLM框架使得可以独立于分布选择链接函数特征。如何选择正确的链接函数?没有完美的标准。您需要考虑有关目标分布的知识,以及理论考虑因素以及模型与实际数据的匹配程度。对于某些数据,规范链接函数可能会导致对该数据无效的值。在指数分布的情况下,规范链接函数是负逆,其可以导致在指数分布的域之外的否定预测。
非线性效应 - GAM
世界不是线性的。线性模型中的线性意味着无论实例在特定特征中具有什么值,将值增加一个单位始终对预测结果具有相同的影响。可以合理地假设在10摄氏度时将温度升高一度对租赁自行车的数量有同样的影响,因为当它已经有40度时,温度会升高吗?直观地说,人们期望将温度从10摄氏度提高到11摄氏度会对自行车租赁产生积极影响,从40到41会产生负面影响,这也是如此,正如您将在本书的许多示例中看到的那样。温度特性对租赁自行车的数量有线性的积极影响,但在某些时候它会变平,甚至在高温下也会产生负面影响。线性模型并不关心,它将尽职尽责地找到最佳线性平面(通过最小化欧几里德距离)。
您可以使用以下技术之一建模非线性关系:
简单转换特征(例如对数)
特征分类
广义加法模型(GAM)
为什么不“简单地”允许(广义)线性模型学习非线性关系? 这就是GAM背后的动机。 GAM放宽了关系必须是简单加权和的限制,而是假设结果可以通过每个特征的任意函数的总和来建模。 数学上,GAM中的关系如下所示:
![]()
该公式类似于GLM公式,不同之处在于线性项βjxj被更灵活的函数fj(xj)代替。 GAM的核心仍然是特征效果的总和,但您可以选择允许某些特征与输出之间的非线性关系。 框架也涵盖了线性效果,因为要线性处理特征,您可以将它们的fj(xj)限制为仅采用xjβj的形式。
最大的问题是如何学习非线性函数。答案称为“样条线”或“样条函数”(spline functions)。样条函数是可以组合的函数,以便逼近任意函数。有点像堆积乐高积木来构建更复杂的东西。有许多令人困惑的方法来定义这些样条函数。如果您有兴趣了解更多关于定义样条线的所有方法,我祝您旅途愉快。我不打算在这里详细介绍,我只想建立直觉。理解样条函数对我个人帮助最大的是可视化各个样条函数并查看数据矩阵的修改方式。例如,要使用样条曲线对温度建模,我们会从数据中删除温度特征,并将其替换为4列,每列代表样条函数。通常你会有更多的样条函数,我只是减少了数字用于说明目的。这些新样条曲线特征的每个实例的值取决于实例的温度值。与所有线性效应一起,GAM然后还估计这些样条权重。 GAM还引入了权重的惩罚项,使它们接近于零。这有效地降低了样条的灵活性并减少了过度拟合。然后通过交叉验证调整通常用于控制曲线灵活性的平滑度参数。忽略惩罚项,使用样条曲线进行非线性建模是一种奇特的特征工程。
优点
线性模型的所有这些扩展本身就是一个宇宙。无论您使用线性模型遇到什么问题,您都可能会找到修复它的扩展。
大多数方法已经使用了几十年。例如,GAM已有近30年的历史。来自工业界的许多研究人员和从业人员对线性模型非常有经验。
除了进行预测之外,还可以使用模型进行推理,得出有关数据的结论 - 假设模型假设未被违反。您可以获得权重,显着性检验,预测间隔等的置信区间。
统计软件通常具有非常好的接口,以适应GLM,GAM和更多特殊的线性模型。
许多机器学习模型的不透明性来自1)缺乏稀疏性,这意味着使用了许多特征,2)以非线性方式处理的特征,这意味着您需要不止一个权重来描述效果,以及3)特征之间相互作用的建模。假设线性模型具有高度可解释性但通常不适应现实,扩展提供了一种实现平滑过渡到更灵活模型的好方法,同时保留了一些可解释性。
缺点
线性模型的大多数修改使得模型不易解释。任何不是身份功能的链接功能(在GLM中)都会使解释复杂化;相互作用也使解释复杂化;非线性特征效果要么不太直观(如对数变换),要么不能再由单个数字(例如样条函数)汇总。
GLM,GAM等依赖于有关数据生成过程的假设。如果违反这些规则,权重的解释将不再有效。
基于树的集合(如随机森林或梯度树增强)的性能在许多情况下比最复杂的线性模型更好。