自动控制原理笔记
首先分析一下,自动控制原理这门学科研究的就是系统的稳定性
通过构建系统的数学模型,并通过不同的分析方法来分析并且校正系统
所以学的就是模型的构建和系统的分析(主要矛盾)
simulink教程
1.自动控制系统的分类
对于自动控制系统有多种分类方法
如按控制方式分可以分为开环控制,反馈控制,复合控制等;
按元件类型可分为机械系统,电气系统,机电系统,液压系统,气动系统,生物系统等
按系统功能分可分为温度控制系统,压力控制系统,位置控制系统等
按系统性能可分为线性系统和非线性系统,连续系统和离散系统,定常系统和时变系统,确定性系统和不确定性系统等
按输入量变化可分为恒值控制系统,随动系统,和程序控制系统等
1.稳定性
2.快速性
3.准确性
3.自动控制的数学模型
1.静态条件下(变量各阶导数为零),描述变量之间关系的代数方程脚静态数学模型,描述变量各阶倒数之间关系的微分方程叫动态数学模型
2.建立控制系统数学模型的方法有 分析法 和 实验法 两种,自控原理这本书用的是分析法
3.时域中常用的数学模型有微分方程,差分方程和状态方程;复数域中有传递函数,结构图;频域有频率特性
时域数学模型
常用的电气元件,力学元件微分方程的建立P21-24
掌握要点:电感电容电阻的电压电流表达式,基尔霍夫定律,电枢回路电压平衡方程,电磁转矩方程,电动机轴上的转矩平衡方程,牛顿运动定律,阻尼力表达式,弹力表达式...
控制系统的微分方程的建立
先由系统原理图画出系统方块图,并分别列写组成系统元件的微分方程,然后,消去中间变量变得到描述系统输出量与输入量之间关系的微分方程。
注意1.信号传递的单向性2.前后级元件的影响
线性微分方程的特性:可叠加性
线性微分方程的求解(重点):
1.考虑初始条件,对微分方程中的每一项分别进行拉氏变换,将微分方程转换为变量s的代数方程
2.由代数方程求出输出量拉氏变换函数的表达式
3.对输出量拉氏变换函数求反变换,得到输出量的时域表达式,即为所求微分方程的解
非线性方程的线性化
复数域数学模型
传递函数的定义:零初始条件下,系统输出量的拉氏变换与输入量的拉式变换之比
传递函数的性质:m≤n,且所有系数均为实数
传递函数的零极点:传递函数的零极点分布图可以更形象的反应系统的全面特性。
传递函数的极点就是微分方程的特征根,因此他们决定了所描述系统自由运动的模态而且在强迫运动中(即零初始条件响应)也会包含这些自由运动的模态。
传递函数的零点并不形成自由运动的模态,但它们却影响各模态在响应中所占的比重,因而也影响曲线的形状。
除了零、极点这种数学模型之外,还有一种数学模型是以典型环节的形式来表述的,也就是说 这个系统的数学模型,
我们能够把它写做:传递函数 等于 由一些比例环节或者是一阶的微分环节或者是二阶的微分环节 比上 积分环节或者一
阶惯性环节或者二阶的震荡环节等等,这样的形式来表示的,这样的数学模型的形式,我们在频域分析法当中经常会见到。
控制系统的结构图与信号流图
控制系统的结构图包含四个基本单元:
1.信号线2.引出点(或测量点)3.比较点(或综合店)4.方框(或环节)
结构图的简化
1.串联方框的简化2.并联方框的简化3.反馈连接方框的简化4.比较点和引出的移动
简化规则P44-45
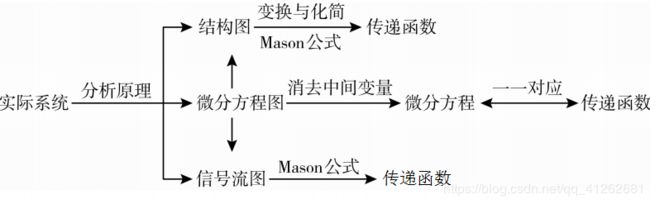
方法1 求系统的传递函数,我们可以先分析系统的工作原理,利用它的工作原理列出它的动态结构图,
然后利用动态结构图的化简或者是直接在动态结构图当中利用Mason公式,我们可以求得系统的传递函数。
方法2 除此之外,如果现在我们得到的数学模型是时域当中的微分方程,只要对这样的微分方程消去中间变量,
然后得到一个仅仅与输入和输出有关的这样一个微分方程,我们只要把微分算子使用s来取带,
一样可以得到系统的传递函数。
方法3 当然,如果系统的数学模型得到的是信号流图,我们可以在信号流图上面直接利用 Mason增益公式
来求解系统的传递函数。
常见的模型
无源网络(比如:RLC电路)、有源网络(比如:由理想运放搭建而成的模拟电路)、简单的电气控制系统(比如:简单的电力拖动、一些电力控制系统),简单力学系统等。
电路通常用到电路元件复数域(复阻抗法)
R - R,L - sL,C - 1/sC
第三章 时域分析方法
1.系统时间响应的性能指标
1.典型输入信号:便于数学分析和实验研究
单位阶跃函数
单位斜坡函数
单位加速度函数
单位脉冲函数
正弦函数
2.动态过程和稳态过程
动态过程:动态过程又称为过渡过程或瞬态过程,指系统在典型输入信号作用下,系统输出量从初始状态到最终状态的响应过程.
稳态过程:稳态过程指系统在典型输入信号作用下,当时间t趋于无穷时,系统输出量的表现方式。
3.动态性能和稳态性能
动态性能
上升时间tr 想用从终值10%上升到终值90%所需的时间;对于有振荡的系统,也可理解为响应从零上升到终值所需的时间。
上升时间越快,响应速度越快
峰值时间tp:指响应超过其终值到达第一个峰值所需的时间
调节时间ts 指响应到达并保持在终值+-5%内所需要的最短时间
超调量σ% 值响应的最大偏移量c(tp)与最终值c(∞)的差与终值c(∞)比的百分数
稳态性能
稳态误差是描述系统稳态性能的一种性能指标
运动方程的阶数通常和系统中储能机构的个数有关
2.一阶系统的时域分析
一阶方程作为运动方程的控制系统,称为一阶系统。有些高阶系统的特性,通常可以用一阶系统的特性来近似表征。
对于不同形式的一阶系统,其响应特性的数学表达式具有不同的物理意义
传递函数为1/(Ts+1)
1.一阶系统的单位阶跃响应
c ( t ) = 1 − e − t / T c(t)=1-e^{-t/T} c(t)=1−e−t/T
T反映系统的额惯性,惯性越小,响应速度越快,惯性越大,响应速度越慢

T=1
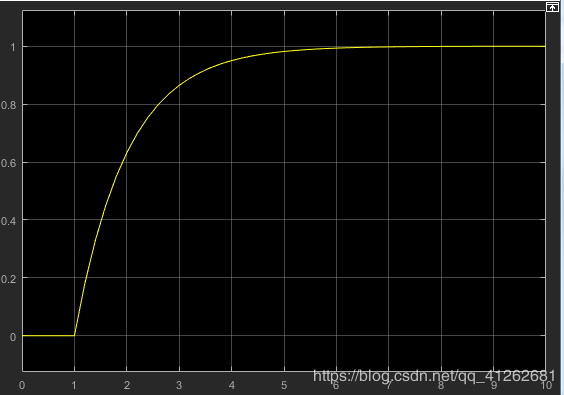
T=2

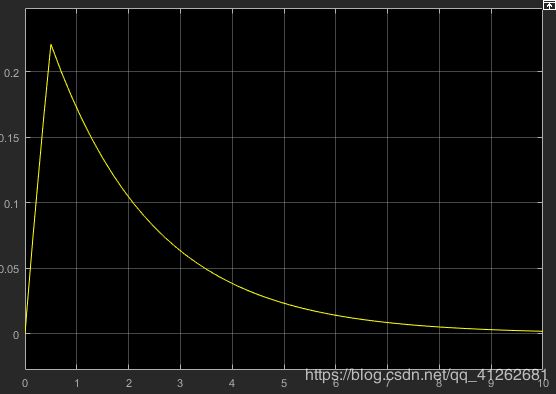
2.一阶系统的单位脉冲响应
c ( t ) = 1 / T e − t / T , t > = 0 c(t)=1/Te^{-t/T},t>=0 c(t)=1/Te−t/T,t>=0
惯性越小,响应速度越好
T=1

T=2
3.一阶系统的额单位斜坡响应
c ( t ) = ( t − T ) + T e − t / T , t > = 0 c(t)=(t-T)+Te{-t/T},t>=0 c(t)=(t−T)+Te−t/T,t>=0
稳态分量是与输入斜坡函数斜率相同但时间滞后T的函数

研究线性定常系统的时间响应,不必对每种输入信号形式进行测定和计算,只需要选取一种典型形式研究
3.二阶系统的时域分析
二阶系统极为普遍,不少高阶系统的特性在一定条件下可用二阶系统的特性来表征。
二阶系统的标准形式
Φ ( s ) = C ( s ) R ( s ) = ω n 2 s 2 + 2 ζ ω n s + ω n 2 \Phi(s)=\frac{C(s)}{R(s)}=\frac{\omega_n^2}{s^2+2\zeta \omega_ns+\omega_n^2} Φ(s)=R(s)C(s)=s2+2ζωns+ωn2ωn2
令分母 s 2 + 2 ζ ω n s + ω n 2 s^2+2\zeta \omega_ns+\omega_n^2 s2+2ζωns+ωn2=0得到二阶系统的两个极点为
s1,2= − ζ ω n + − ω n ζ 2 − 1 -\zeta\omega_n+-\omega_n\sqrt{\zeta^2-1} −ζωn+−ωnζ2−1

ζ < 0 \zeta<0 ζ<0,不稳定
0 < ζ < 1 0<\zeta<1 0<ζ<1,欠阻尼
ζ = 1 \zeta=1 ζ=1,临界
ζ > 1 \zeta>1 ζ>1,过阻尼