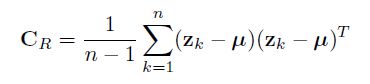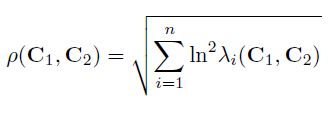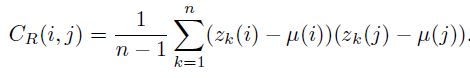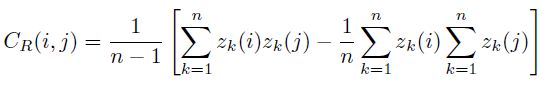Region Covariance: A Fast Descriptor for Detection and Classification算法总结
传统的像素级特征比如颜色、梯度、滤波响应等等它们对光照变化和非刚性运动的描述不够鲁棒,而在像素级特征之上延伸出的直方图表述了一种无参的联合分布,然而随着特征数目的增加,联合分布的表达是呈指数增加的。另外,关键点的检测以及描述在匹配局部图像上非常有效,然而它们只包含了局部信息,没有利用全局的信息。
与直方图类似,协方差也能作为特征描述,并且协方差的特征维度要小很多。实验证明,协方差特征比其他特征性能要优越。
协方差矩阵提取算法流程如下:
1. 计算图像的特征矩阵
I表示原图像,可以是灰度图也可以是彩色图。I的大小为W*H,令d为特征维度,那么F的维度为W*H*d。提取的特征可以是亮度、颜色、梯度、滤波响应等等的级联。
2. 计算特征协方差矩阵
n为图像中像素总个数,Zk表示第k个像素点的特征,d*1维向量,u为特征的均值,也是d*1维,所以协方差矩阵的维数为d*d,大大降低了特征维度。
3. 计算协方差的相似度
由于协方差矩阵不属于欧式空间,所以并不能将此特征应用于那些常用的依赖于欧式空间的机器学习方法中,可以依据上式来计算两个特征的相似度,其中
![]() 是C1和C2的特征值,用下式来计算:
是C1和C2的特征值,用下式来计算:
且Xi不等于0。相似度越小表明两个特征越相似,当且仅当两个特征相等的时候相似度为0。
补充说明:
1.用协方差矩阵来作为区域的描述已足够,它对视角以及姿态的轻微改变有一定的鲁棒性。
2.它是多种特征的融合,展现了它们一定的相关性。协方差矩阵对角元素表明了每种特征的方差,非对角元素表明了它们之间的相关性。
3.它对个别像素受到噪声干扰的情况也有鲁棒性,因为协方差的计算是求平均的过程。
4.协方差矩阵并不完全具有旋转、尺度不变性,比如当基本的特征中包含像素点方向信息时,旋转不变性不再适用,尺度不变也是类似的。应该具体问题具体对待选择合适的基本特征。
积分图快速计算方法:
由于协方差矩阵中第(i,j)个元素可以写成如下形式:
根据均值的定义,上式可以简化为:
因此我们可以构造出d+d2个积分图像,其中表示z(i)的有d个积分图,表示z(i)z(j)的有d2个。
整个图像的积分图表示为:
简写成:
图像的平方积分图表示为:
简写成:
所以协方差矩阵可以写成:
其中:
![]()
应用——对象检测:
博主最近正好在研究图像比对识别问题,与论文中第三节内容相似,故也总结一下文中方法,第四节分类问题不在此赘述。
在对象检测问题中,给定一个目标图像,我们需要在任意的其他图像中找到并定位目标图像。文中使用的特征是像素位置、颜色、一阶导数、二阶导数,组成了一个9维特征。
其中导数可以通过[-1,0,1]和[-1,2,-1]来计算。协方差矩阵是9*9维的。
对于一个目标图像,用5个协方差矩阵来表述:
首先计算全局图像的协方差C1,使用滑窗的方法来定位。在每个位置我们分析9个不同尺度大小的滑窗来精确定位,其中4个比原图像小,4个比原图像大,相邻尺度之间的比例为15%,在最小的尺度上每次滑动的距离为3个像素,相邻尺度之间滑动的增加距离也为15%。这样我们通过C1选择出1000个最相近的目标位置,然后我们利用C1-C5在这1000个位置里继续搜索,差异度通过下式来计算:
该表达式实质上是舍弃了最不匹配的协方差矩阵,并对另外4个的相似度求和,这样做的目的是提高了对遮挡和光照的变化的鲁棒性。最后差异度最小的区域作为匹配的区域。
协方差特征比直方图计算快且效果好,在C++下能够达到实时。