动手学习深度学习pytorch版——多层感知机与softmax层

  本系列是基于亚马逊李沐老师的教材《动手学习深度学习》，以及 李沐老师对应的视频教程内容展开。但是李沐老师课程中使用的深度学习框架是MXNet，其实选择什么框架并不是重点，重点应该是其中的内容。课程既然叫动手学习深度学习，那当然要动手操作。用MXNet重复一遍教材内容并没有很好的学习效果，另外，我本身还是更喜欢使用pytorch框架，因此，希望将该教材的内容用pytorch实现一遍，并学习相关的知识内容。希望能给其他喜欢pytorch的读者一些帮助。 代码开源供学习使用，如引用请注明出处，谢谢。

1. 内容简介

  在“线性回归”章节的内容中，我们介绍了如何实现一个属于自己的线性层，并用自己简单生成的数据集进行了验证，了解了一些有关深度学习训练和pytorch框架的基本知识。在本篇内容中，我们将使用更接近现实情况的数据集，并搭建一个更复杂的神经网络，来完成一个分类问题。

1.1 数据集介绍

  使用的数据集是Fashion_MNIST，该数据集共有70000个样本，60000个样本作为训练集，10000个样本作为测试集。70000个样本中，总共包含10种类别的常见物品(见下图)。每张图片的尺寸是28*28的，所以我们可以将图片张开成为1×784的一维向量，作为我们网络的输入。网络的输出就是1×10的向量，向量中的每个元素都可以理解为属于每个种类的预测概率，比如向量的第一个元素代表输入图像属于pullover类别的概率。

1.2 多层感知机(MLP,Multilayer Perceptron)介绍

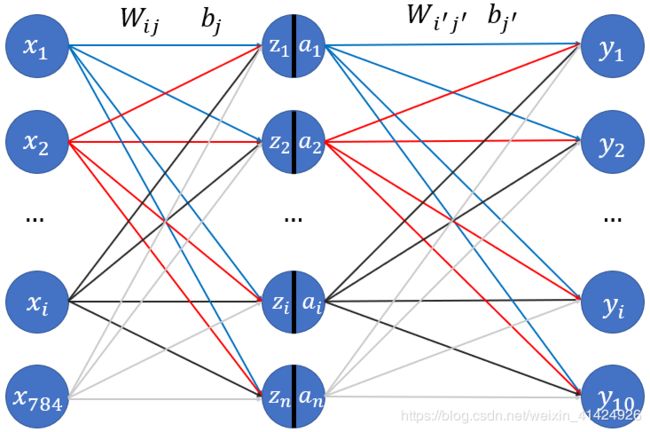
  多层感知机其实就是多个线性层叠加起来的网络，这里我们以两个线性层叠加为例子。第一个线性层的输入就是图像像素个数，也就是784，每个像素都代表输入样本的一个特征，如下图的$x_1-x_{784}$。非输入和输出的层为我们称为隐藏层，如下图的$z_1-z_n$，其中这里的n取1000。然后，经过第一个线性层的计算后，输入数据应当从784个特征转化成了1000个特征，再将这1000个特征输入到第二个线性层中，第二个线性层输出维度为10，代表每个类别的概率。具体结构图如下：

  注意到上图中有几个特点：

• 图中每个结点可以当作一个神经元。每层的输入神经元和所有的输出神经元都有一条线连着，每条线上都有一个权值$W_{ij}$，表示输入的第i个神经元与输出的第j个神经元的权值系数。另外，每个输出神经元都配有一个偏置系数$b_j$。所以，一个输出神经元对应所有输入神经元的结构，就是我们在“线性回归”里使用的简单线性层。这里只是把线性层的输出神经元个数变成了n个。那么，对应于每个输出神经元$z_i$，其计算公式为：
  $$z_j=x\times W_{:,j}$$

  其中，x是输入向量，$W_{:,j}$是W矩阵第j列的列向量。

• 在隐藏层的神经元中，除了$z_i$外，还有$a_i$，是什么呢？$a_i$是$z_i$经过激活函数激活后的数值，假设激活函数是$\sigma (x)$，那么就有：
  $$a_i=\sigma (z_i)$$
  常用的激活函数在下文中会介绍。这里说明一下为什么要激活函数，因为如果不使用激活函数，那么其实上述网络的输出就是$y=(x\times W+b)\times W^{\prime }+b^{\prime }\iff y=x\times W_{new}+b_{new}$，也就是说，无论你叠多少层线性层，如果不加激活函数，那么其实和只有一层线性层是等价的。而加入了激活函数后，通常激活函数是非线性的，所以就有：
  $$y=\sigma (x\times W+b)\times W^{\prime }+b^{\prime }$$
  这样，整个网络的映射就具备了非线性能力，不再等价于普通的线性层了。注意，最后一层线性层的输出通常就不需要激活函数激活了，对于分类问题，会使用下文提到的Softmax层进行归纳总结。
• 图中所有的$W_{ij},W_{i^{\prime }{j}^{\prime }},b_j,b_{j^{\prime }}$都是网络的参数，都是需要进行训练更新的。

1.3 激活函数

  激活函数其实种类特别特别多，有时间再专门介绍各种激活函数的特点及对比。这里就介绍最基本的三种：
  1).Sigmoid函数
$$\sigma (x)=\frac{1}{1+e^{-x}}$$

  这是最早的激活函数。

  2).ReLU函数

$$\sigma (x)=max(x,0)$$

  看起来就是简单的取最大值函数，但是因为它具有计算简单且性能较好的特性，是使用的最广泛的激活函数。

  3).tanh函数
$$\sigma (x)=\frac{1-e^{-2x}}{1+e^{-2x}}$$

1.4 Softmax层

  先说明一下Softmax层的计算方法：
  假设网络的输出是$y=(y_1,y_2,...,y_{10})$，分别代表输入样本x对应于每个类别的概率，那么softmax的计算方式为：
$$y_i^{\prime }=\frac{e^{y_i}}{{\sum }_{i=1}^{10}{e}^{y_i}},输出值域为y_i^{\prime }\in [0,1]$$

  简单来说就是先以所有输出为指数求e为底的指数数值，然后再进行标准化，使得${\sum }_{i=1}^{10}{y}_i^{\prime }=1$。这种标准化操作还是很好理解的，就是让输出变成对应每个类别的相对概率，比如$y_1^{\prime }=0.5$则说明该样本属于第一类的情况，在它相对于属于其他所有类的情况中，出现的概率为0.5。
  为什么Softmax要用e指数进行标准化，而不是其他方式(如min-max方式)？
  其实softmax的公式是基于最大熵模型理论的。最大熵模型简单来说就是：在已知部分知识的前提下(也就是已知网络输出的十个数值)，关于未知分布(也就是样本属于十个类别的概率)最合理的推断就是符合已知知识最不确定或最随机的推断（也就是熵值最大)。其原则是承认已知事物（知识），且对未知事物不做任何假设，没有任何偏见。而已知网络的输出，求其真实概率分布的最大熵模型的解，就是softmax的表达式。
  也就是说，网络输出了十个数值，我们希望用这十个数值来求出样本属于每个类别最合理的概率模型，这个模型理论上来说就是最大熵模型，其求解公式就是softmax的数学表达式。

1.5 交叉熵损失函数

  假设随机变量X，其对应的真实概率密度是p(x)，模型预测的概率密度是q(x)。
  KL散度(相对熵)是度量模型预测的结果信息量和真实事件的信息量之间的差值，即熵差。
$$KL(p||q)=\sum _i[p(x_i)\log \frac{p(x_i)}{q(x_i)}]=\sum _{i}p(x_i)\log p(x_i)-\sum _{i}p(x_i)\log q(x_i)=H(p,q)-H(p)$$

  前一部分是真实事件的熵值，为定值，后一部分就是交叉熵：
$$交叉熵：H(p,q)=-\sum _{i}p(x_i)\log q(x_i)$$

  可以理解为用预测的概率分布$q(x_i)$代替真实分布$p(x_i)$，来求解事件的熵值。因为两个分布交叉使用，所以叫交叉熵。交叉熵大于真实事件的熵值。
  从上述表达式可以看出，$\because H(p,q)\ge H(p)$，所以交叉熵越小，样本预测概率越接近真实概率。因此，将每个样本的交叉熵作为损失值，然后取均值，就是交叉熵损失函数：
$Loss=-{\sum }_{i=1}^m{\sum }_{j=1}^{10}p(x_j^{(i)})\log q(x_j^{(i)})=-\frac{1}{m}{\sum }_{i=1}^m{\sum }_{j=1}^{10}{y}_j^{(i)}\log {\hat{y}}_j^{(i)}$

  实际使用的时候，看起来好像是求和，但是其实$y^{(i)}=(y_1^{(i)},y_2^{(i)},...,y_{10}^{(i)})$中只有一个是1，其余全是0，所以其实$loss=-\log {\hat{y}}_j^{(i)}$，其中的下标j对应于$y_j^{(i)}=1$。

1.6 网络的最终输出

  经过上述折腾，最终网络经过softmax层会输出$y=(y_1,y_2,...,y_{10})$，且${\sum }_{i=1}^{10}{y}_i=1$。此时，选择其中最大的$y_i$，其对应的标签序号 $i$ 就是网络最终预测的分类类别。

2. 多层感知机——从零开始

2.1 激活函数的代码实现

def my_relu(inputs):
    """将输入数据inputs与和inputs维度相同的全零tensor比较，每个位置取两者的较大值"""
    return torch.max(inputs,torch.zeros_like(inputs))


def my_sigmoid(inputs):
    # 必须保证输入的tensor数据类型是float，否则计算会失去意义
    if inputs.type()!=torch.FloatTensor:
        inputs = inputs.float()
    return 1.0 / (1 + torch.exp(-inputs))


def my_tanh(inputs):
    # 必须保证输入的tensor数据类型是float，否则计算会失去意义
    if inputs.type()!=torch.FloatTensor:
        inputs = inputs.float()
    return (1 - torch.exp(-2 * inputs)) / (1 + torch.exp(-2 * inputs))

2.2 softmax层的代码实现

def my_softmax(inputs):
    """计算输入的inputs数据的softmax，并返回计算后的数值"""
    inputs.exp_()
    m = inputs.size()[0]
    # 因为输入softmax层的是m×10的张量，其中m是batchsize的样本数量
    # 需要inputs张量中的每个元素都除以对应行的元素之和，所以在对inputs张量的每行求和后，需要repeat成(m,10)的矩阵
    # 这样就可以实现原始计算目标
    inputs_sum = torch.sum(inputs,dim=1).reshape(m,1).repeat((1,10))
    return inputs/inputs_sum

2.3 交叉熵损失函数的计算

def my_cross_entropy_loss(preds,labels):
    """交叉熵损失函数"""
    # preds[i,j]存放的是第i个样本，其对应属于第j类的预测概率
    # labels是(m,1)的列向量，对应于样本的标签，10类所以labels是0-9的整数
    m = labels.size()[0]
    return torch.sum(-torch.log(preds[list(range(m)),labels]))/m

2.4 线性层模块的定义

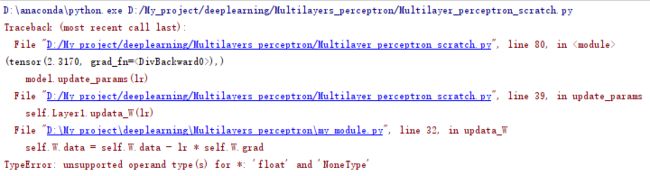
  和“线性回归”章节中的网络类很相似，稍微进行了一些修改。线性层中的权值和偏置都乘0.01是因为，最后一个线性层的网络输出要经过softmax层，而softmax的计算是包含指数e为底的幂次计算，如果网络输出数值过大，很容易导致softmax之后的结果全为nan(如下图)。因此，为了让网络初始的时候输出的数值减小一些，就需要将网络参数的初始化数值减小，所以乘了0.01。

  另外，设置系数w,b的requires_grad()属性的顺序需要非常注意，如果顺序不对，则会出现如下图所示的错误信息，警告你系数的梯度不存在。

class my_Linear(object):
    """线性层"""
    def __init__(self, inputs_num, outputs_num, is_cuda=False):
        """初始化线性层参数
        :param inputs_num: 线性层输入神经元个数
        :param outputs_num: 线性层输出神经元个数
        :param is_cuda: 是否使用GPU计算
        """
        if is_cuda:
            # 在送进cuda前如果设置requires_grad=True，送进cuda后则is_leaf会变为False
            # 而pytorch默认最终只会保留叶子结点的梯度，这样会导致系数的梯度被清空，无法更新，所以要注意顺序
            self.W = 0.01 * torch.randn((inputs_num, outputs_num)).cuda()
            self.b = 0.01 * torch.randn((1, outputs_num)).cuda()
            self.W.requires_grad_()
            self.b.requires_grad_()
        else:
            # 就算下面式子改成self.W = 0.01 * torch.randn((inputs_num,outputs_num),requires_grad=True)
            # 在训练的时候还是会出问题，系数的梯度会清零，因为torch.randn()是一个张量，它是计算图的叶子节点，其梯度会保存
            # 而0.01 * torch.randn()是一个新的张量，它已经不是叶子节点了，所以它的梯度不会保存
            # 乘0.01是因为要做softmax，权值系数的初始化不能太大，否则会导致网络输出的数值爆炸
            self.W = 0.01 * torch.randn((inputs_num,outputs_num))
            self.b = 0.01 * torch.randn((1,outputs_num))
            # 所以要在计算完后，重新定义self.W.requires_grad_，让self.W变成可导的且其is_leaf=True,使其梯度不要清零
            self.W.requires_grad_()
            self.b.requires_grad_()

    def forward(self,X):
        X = torch.mm(X,self.W)+self.b
        return X

    def __call__(self,X):
        return self.forward(X)

    def updata_W(self,lr):
        self.W.data = self.W.data - lr * self.W.grad
        self.b.data = self.b.data - lr * self.b.grad

    def zero_grad(self):
        if self.W.grad is not None:
            self.W.grad.zero_()

        if self.b.grad is not None:
            self.b.grad.zero_()

2.5 多层感知机网络的代码实现

  为了简单起见，下面的代码只采用了两层线性层，感兴趣的读者可以自行增加更多的线性层，使用不同的激活函数，来看看网络的效果。

class MLP_Net(object):
    def __init__(self, inputs_num, outputs_num, AF_type='relu', is_cuda=False):
        """
        初始化
        :param inputs_num: 网络输入的维数
        :param outputs_num: 网络输出的维数
        :param AF_type: 网络中使用的激活函数类型，['relu','sigmoid','tanh']三种供选择
        """
        self.Layer1 = my_Linear(inputs_num, 1000, is_cuda)
        self.Layer2 = my_Linear(1000, outputs_num, is_cuda)
        self.AF_dict = {"relu":my_relu, "sigmoid":my_sigmoid, "tanh":my_tanh}  # 创建包含3种激活函数的字典
        self.AF_type = AF_type

    def forward(self, inputs):
        inputs = self.Layer1(inputs)
        inputs = self.AF_dict[self.AF_type](inputs)  # 根据AF_type的输入，选择对应的激活函数进行激活
        inputs = self.Layer2(inputs)
        inputs = my_softmax(inputs)
        return inputs

    def __call__(self, inputs):
        return self.forward(inputs)

    def update_params(self, lr):
    	"""更新网络参数，就是更新每一个线性层内部的参数"""
        self.Layer1.updata_W(lr)
        self.Layer2.updata_W(lr)

    def zero_grad(self):
    	"""将每一个线性层内部参数的梯度归零"""
        self.Layer1.zero_grad()
        self.Layer2.zero_grad()

2.6 数据集的获取

  由于pytorch对应的torchvision.datasets中有提供Fashion_MNIST的数据集载入，所以这里就不再麻烦自己创建数据集的Dataset类了，直接使用提供好的API下载并导入数据。当然，读者可以自己下载对应数据集，并自己完成数据的导入和Dataset类的创建，提高自己的熟练度。另外说明一下，pytorch导入的FashionMNIST数据集，已经帮你把图片标准化过了，也就是图片中的像素数值全都是[0,1]范围内的数值，而不是[0,255]。数据导入的代码如下：

from torchvision import datasets,transforms
def data_load():
    train_Data = datasets.FashionMNIST("../datasets/Fashion_MNIST/", download=True, transform=transforms.ToTensor()) # transform是对数据进行预处理，这里是将图片数据转化为tensor类型
    test_Data = datasets.FashionMNIST("../datasets/Fashion_MNIST/", download=True, train=False, transform=transforms.ToTensor())
    return train_Data, test_Data

2.7 开始训练啦

if __name__ == '__main__':
    train_set, test_set= data_load()
    epoch = 10
    batchsize = 100
    lr = 0.01
    model = MLP_Net(28*28, 10, AF_type='relu')
    train_dataloader = DataLoader(train_set, batch_size=batchsize, shuffle=True)
    test_dataloader = DataLoader(test_set, batch_size=1, shuffle=False)

    # 训练过程可视化，需要开启visdom
    is_vis = False
    if is_vis:
        vis = visdom.Visdom()
        viswin1 = vis.line(np.array([0]), np.array([0]),
                           opts=dict(title="Training acc/epoch", xlabel="epoch", ylabel="accuracy"))
        viswin2 = vis.line(np.array([0]), np.array([0]),
                           opts=dict(title="Test acc/epoch", xlabel="epoch", ylabel="accuracy"))

    it = 0
    acc_x = np.zeros((epoch+1,2))
    acc_y = np.zeros((epoch+1,2))
    for e in range(epoch):
        acc = 0
        for x,y in train_dataloader:
            it += 1
            x = x.reshape(batchsize,-1)
            # x = x.cuda()
            # y = y.cuda()
            pred = model(x)
            loss = my_cross_entropy_loss(pred,y)
            model.zero_grad()
            loss.backward()
            model.update_params(lr)
            print("epoch %d | loss = %.2f"%(e,loss.item()))
            pred = torch.argmax(pred, dim=1)
            pred = pred.long()
            pred[pred!=y]=0
            pred[pred>0]=1
            acc += torch.sum(pred)

        acc = acc.float()
        acc_y[e+1,0] = acc.numpy()/60000.0
        acc_x[e+1,0] = e+1
        if is_vis:
            vis.line(np.array([acc/60000.0]),np.array([e+1]), viswin1, update='append')

        acc = 0
        n = 0
        for x,y in test_dataloader:
            x = x.reshape(1,-1)
            # x = x.cuda()
            # y = y.cuda()
            pred = model(x)
            pred = torch.argmax(pred,dim=1)
            n += 1
            pred = pred.long()
            if pred==y:
                acc += 1
        print("*******************************************************")
        print("acc:%.2f"%(1.0*acc/n))
        print("*******************************************************")
        acc_y[e+1,1] = 1.0*acc/n
        acc_x[e+1, 1] = e + 1
        if is_vis:
            vis.line(np.array([1.0*acc/n]), np.array([e+1]), viswin2, update='append')
    if is_vis:
        vis.line(acc_y,acc_x,opts=dict(title="compare acc/epoch", xlabel="epoch", ylabel="accuracy"))

3.多层感知机——pytorch版

3.1 多层感知机网络模块的搭建

  可以看到，使用pytorch框架为我们搭建网络省了很多事，你只要按网络结构把所需要的网络层都叠加在nn.Sequential()里面就可以了，注意，Sequential里不同的网络层之间有逗号分隔。还要注意网络的上下层之间，通道数要一一对应，也就是上层网络的输出通道数要等于下层网络的输入通道数。如果需要激活，就在需要激活的网络层后面加上对应的激活函数层。softmax也是一样。

class MLP_Net(nn.Module):
    def __init__(self, inputs_num, outputs_num, AF_type=None):
        super(MLP_Net,self).__init__()
        self.Layer = nn.Sequential(
            nn.Linear(inputs_num, 1000),
            nn.ReLU(),  # 激活函数层
            nn.Linear(1000, outputs_num),
            nn.Softmax()  # softmax层
        )

    def forward(self, inputs):
        return self.Layer(inputs)

3.2 开始训练啦

  其实用pytorch提供的模块进行训练的代码和之前从零开始的训练代码非常类似。只是由于pytorch提供了损失函数和优化器的API，所以不需要再定义损失函数和优化器，只需要直接使用就可以了。具体代码如下：

if __name__ == '__main__':
    train_set, test_set= data_load()
    epoch = 10
    batchsize = 100
    lr = 0.01
    model = MLP_Net(28*28, 10, AF_type='relu')
    train_dataloader = DataLoader(train_set, batch_size=batchsize, shuffle=True)
    test_dataloader = DataLoader(test_set, batch_size=1, shuffle=False)

    # 训练过程可视化
    is_vis = False
    if is_vis:
        vis = visdom.Visdom()
        viswin1 = vis.line(np.array([0]), np.array([0]),
                           opts=dict(title="Training acc/epoch", xlabel="epoch", ylabel="accuracy"))
        viswin2 = vis.line(np.array([0]), np.array([0]),
                           opts=dict(title="Test acc/epoch", xlabel="epoch", ylabel="accuracy"))

    it = 0
    acc_x = np.zeros((epoch+1,2))
    acc_y = np.zeros((epoch+1,2))
    criterion = nn.CrossEntropyLoss()   ###定义交叉熵损失###
    optimizer = torch.optim.SGD(model.parameters(),lr=lr)   ###定义优化器###
    for e in range(epoch):
        acc = 0
        model.train()  ###设置网络的使用模式###
        for x,y in train_dataloader:
            it += 1
            x = x.reshape(batchsize,-1)
            # x = x.cuda()
            # y = y.cuda()
            pred = model(x)
            loss = criterion(pred,y)
            optimizer.zero_grad()  ###优化器梯度清零###
            loss.backward()
            optimizer.step()  ###优化器更新参数###
            print("epoch %d | loss = %.2f"%(e,loss.item()))
            pred = torch.argmax(pred, dim=1)
            pred = pred.long()
            pred[pred!=y]=0
            pred[pred>0]=1
            acc += torch.sum(pred)

        acc = acc.float()
        acc_y[e+1,0] = acc.numpy()/60000.0
        acc_x[e+1,0] = e+1
        if is_vis:
            vis.line(np.array([acc/60000.0]),np.array([e+1]), viswin1, update='append')

        acc = 0
        n = 0
        model.eval()  # 设置网络为inference模式
        for x,y in test_dataloader:
            x = x.reshape(1,-1)
            # x = x.cuda()
            # y = y.cuda()
            pred = model(x)
            pred = torch.argmax(pred,dim=1)
            n += 1
            pred = pred.long()
            if pred==y:
                acc += 1
        print("************************************************************************************************")
        print("acc:%.2f"%(1.0*acc/n))
        print("************************************************************************************************")
        acc_y[e+1,1] = 1.0*acc/n
        acc_x[e+1, 1] = e + 1
        if is_vis:
            vis.line(np.array([1.0*acc/n]), np.array([e+1]), viswin2, update='append')
    if is_vis:
        vis.line(acc_y,acc_x,opts=dict(title="compare acc/epoch", xlabel="epoch", ylabel="accuracy"))

4. 结果分析

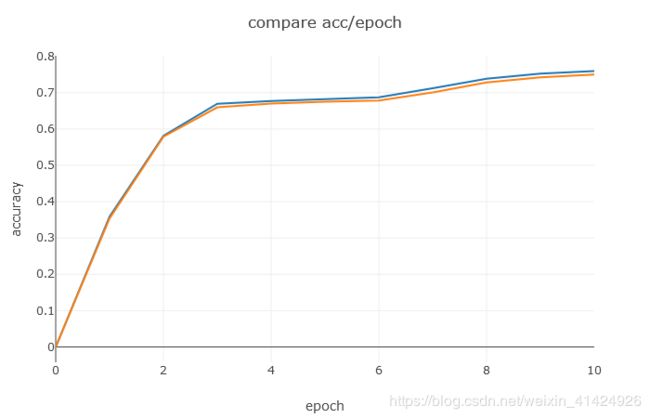
  下图可以看到，我们自己手写的网络，其训练过程看起来更平稳，而且最终的准确率也比pytorch版本的高了大概10个百分点。不仅如此，pytorch版本的网络收敛速度还慢得多，本来打算都跑10个epoch，但是发现pytorch版跑完10个epoch居然还没收敛，因此就跑了25个epoch。其实结果还是蛮惊喜的，这是我这么多次手写代码第一次效果跑赢官方API的一次。原因目前还没找到，有知道的大神可以留言告知一下。从训练过程来看，pytorch搭建的网络它的loss下降的速度也比我们自己写的要慢，尤其是前几轮loss下降的很小。

参数	batchsize=100 lr=0.01	最终测试集准确率
从零开始		0.83
pytorch		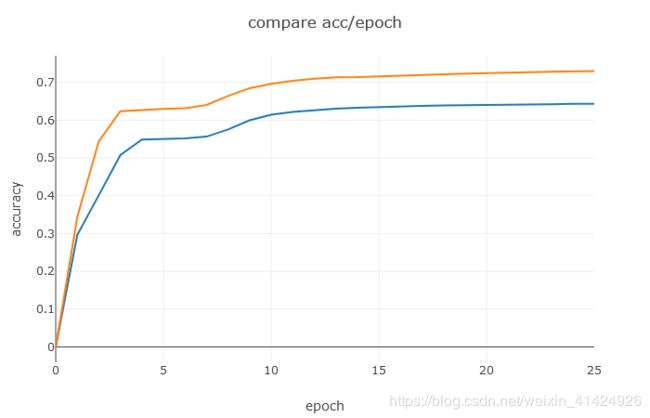0.73

参数	batchsize=10 lr=0.01	最终测试集准确率
从零开始		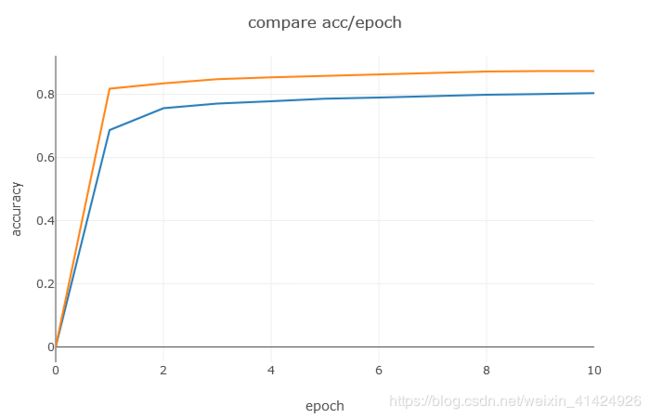0.87
pytorch		0.82

  这里顺便说一下，可能很多人都很奇怪，为什么测试集的准确率会一直高于训练集的准确率？当然，巧合是一种解释；样本没有划分均衡也是有可能导致这种情况的(比如特征比较明显的都划分到测试集里了)。但是，此处最重要的原因是，这里的训练准确率是在训练过程中计算的，这时候，每个batch训练后更新网络参数，再训练下一个batch，网络是一边训练一边更新一边计算准确率的，所以其实这个训练准确率的获取并不是使用一个参数固定的网络，而是一个仍在不断更新进步的网络。而测试集的准确率是在一个epoch结束后才进行测试计算的，这时候对于一个epoch，训练以及结束，网络不再更新，此时的网络应该是当前epoch下的最优网络(最优是相对于当前epoch来说是最优的)，那测试效果当然要比训练过程中使用未达到最优的网络要好一些。最简单的验证方式就是，在一个epoch训练完后，同时那训练集和测试集都进行准确率计算，这时候得到的结果就如下图，这时候就是理想的情况，训练集准确率高于测试集。当然，通常不会这么做，因为这样又要把训练的所有样本预测一遍，非常浪费时间。