84. Largest Rectangle in Histogram. 单调栈

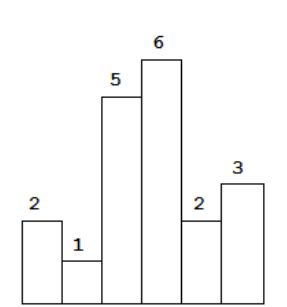
Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

The largest rectangle is shown in the shaded area, which has area = 10 unit.

Example:

Input: [2,1,5,6,2,3]
Output: 10

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/largest-rectangle-in-histogram

1.vecotr几个声明

vector  vec;          //声明一个int型向量
vector  vec(5);       //声明一个初始大小为5的int向量
vector  vec(10, 1);   //声明一个初始大小为10且值都是1的向量

2.解题思路
遍历每个木板，对每一块木板分别向左向右拓展，知道遇见比自身低的木板，然后用高度✖宽度。
使用栈进行求解，从左到右遍历，栈空则入栈，若栈非空，检查栈顶，若栈顶大于等于自身则出栈，直至栈空或者栈顶小于自身。此时栈顶元素的下标即为向左可拓展的最大下标，向右同理。
3.两次遍历改一次遍历
从左向右遍历，出栈时，当前元素下标即为出栈元素的向右可拓展的最大下标。

//2次遍历
class Solution {
public:
    int largestRectangleArea(vector& heights) {
        int n = heights.size();
        vector  left(n),right(n);
        int ans = 0;
        stack  st;

        for (int i = 0;i < n; i++){
            while ( !st.empty() && heights[i] <= heights[st.top()] ){
                st.pop();
            }
            left[i] = st.empty() ? -1 : st.top();
            st.push(i);
        }

        while (!st.empty()) st.pop();

        for (int i = n-1; i >=0 ; i--){
            while ( !st.empty() && heights[i] <= heights[st.top()] ){
                st.pop();
            }
            right[i] = st.empty() ? n : st.top();
            st.push(i);
        }

        for (int i = 0; i < n; i++){
            ans = max( ans, heights[i] * (right[i] - left[i] - 1));
        }

        return ans;
    }
};

//1次遍历
class Solution {
public:
    int largestRectangleArea(vector& heights) {
        int n = heights.size();
        vector  left(n,0),right(n,n);
        int ans = 0;
        stack  st;

        for (int i = 0;i < n; i++){
            while (!st.empty() && heights[st.top()] >= heights[i]){
                right[st.top()] = i;
                st.pop();
            }
            left[i] = st.empty() ? -1 : st.top();
            st.push(i);
        }

        for (int i = 0; i < n; i++){
            ans = max ( ans, heights[i] * (right[i] - left[i] -1));
        }

        return ans;
    }
};