利用Python进行数据分析——NumPy范例

范例：随机漫步

我们通过模拟随机漫步来说明如何运用数组运算。先来看一个简单的随机漫步的例子：从0开始，步长1和－1出现的概率相等。我们通过内置的random模块以纯Python的方式实现1000步的随机漫步：

import random
position=0
walk=[position]
steps=1000
for i in range(steps):
    step=1 if random.randint(0,1) else -1
    position+=step
    walk.append(position)
print(walk)

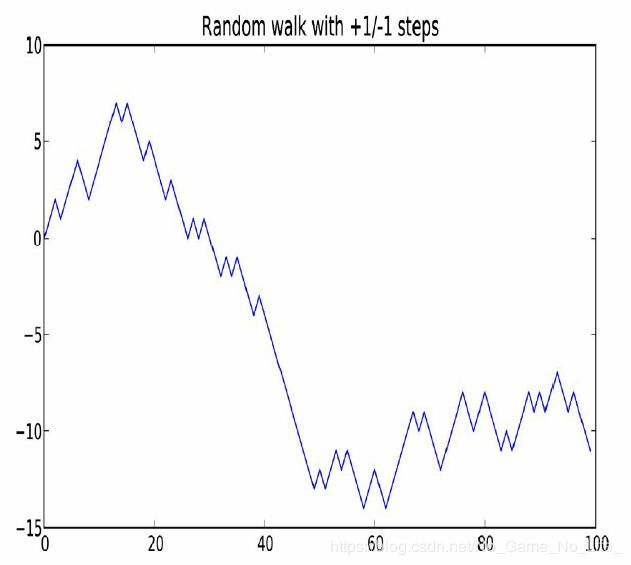
不难看出，这其实就是随机漫步中各步的累计和，可以用一个数组运算来实现。因此，我用np.random模块一次性随机产生1000个“掷硬币”结果（即两个数中任选一个），将其分别设置为1或－1，然后计算累计和：

import numpy as np
nsteps=1000
draws=np.random.randint(0,2,size=nsteps)
steps=np.where(draws>0,1,-1)
walk=steps.cumsum()
print(walk)

output

[ -1  -2  -1   0   1   0   1   0   1   2   3   4   5   6   5   4   3   4
   5   6   5   4   3   4   5   4   5   6   7   6   5   6   7   8   9  10
   9   8   9   8   9  10  11  12  11  10   9   8   9   8   7   8   9   8
    . . .
 -11 -10 -11 -12 -11 -10  -9  -8  -7  -8  -7  -8  -7  -6  -7  -6  -5  -6
  -7  -8  -7  -8  -7  -6  -7  -6  -7  -8]

有了这些数据之后，我们就可以做一些统计工作了，比如求取最大值和最小值：

In [219]: walk.min()
Out[219]: -3
In [220]: walk.max()
Out[220]: 31

现在来看一个复杂点的统计任务——首次穿越时间，即随机漫步过程中第一次到达某个特定值的时间。假设我们想要知道本次随机漫步需要多久才能距离初始0点至少10步远（任一方向均可）。np.abs(walk)>=10可以得到一个布尔型数组，它表示的是距离是否达到或超过10，而我们想要知道的是第一个10或－10的索引。可以用argmax来解决这个问题，它返回的是该布尔型数组第一个最大值的索引（True就是最大值）：

In [221]: (np.abs(walk) >= 10).argmax()
Out[221]: 37

注意，这里使用argmax并不是很高效，因为它无论如何都会对数组进行完全扫描。在本例中，只要发现了一个True，那我们就知道它是个最大值了。

---

一次模拟多个随机漫步
如果你希望模拟多个随机漫步过程（比如5000个），只需对上面的代码做一点点修改即可生成所有的随机漫步过程。只要给numpy.random的函数传入一个二元元组就可以产生一个二维数组，然后我们就可以一次性计算5000个随机漫步过程（一行一个）的累计和了：

import numpy as np
nsteps=1000
nwalks=5000
draws=np.random.randint(0,2,size=(nwalks,nsteps))#5000*1000的数组
steps=np.where(draws>0,1,-1)
walk=steps.cumsum(1)#横轴
print(walk)

output:

[[  1   2   1 ...  30  29  28]
 [ -1   0   1 ...  20  21  20]
 [  1   0   1 ... -64 -63 -62]
 ...
 [ -1  -2  -1 ...  12  13  12]
 [  1   2   1 ...  30  29  30]
 [  1   0   1 ...   6   7   6]]

现在，我们来计算所有随机漫步过程的最大值和最小值：

In [228]: walks.max()
Out[228]: 138
In [229]: walks.min()
Out[229]: -133

得到这些数据之后，我们来计算30或－30的最小穿越时间。这里得要稍微动一下脑筋，因为不是5000个过程都到达了30。我们可以用any方法来对此进行检查：

In [230]: hits30 = (np.abs(walks) >= 30).any(1)
In [231]: hits30
Out[231]: array([False, True, False, ..., False, True, False], dtype=bool)
In [232]: hits30.sum() # 到达30或－30的数量
Out[232]: 3410

然后我们利用这个布尔型数组选出那些穿越了30（绝对值）的随机漫步（行），并调用argmax在轴1上获取穿越时间：

In [233]: crossing_times = (np.abs(walks[hits30]) >= 30).argmax(1)
In [234]: crossing_times.mean()
Out[234]: 498.88973607038122

请尝试用其他分布方式得到漫步数据。只需使用不同的随机数生成函数即可，如normal用于生成指定均值和标准差的正态分布数据。

import numpy as np
nwalks=5000
nsteps=1000
steps=np.random.normal(loc=0,scale=0.25,size=(nwalks,nsteps))
walks=steps.cumsum(1)
hit20=(np.abs(walks)>=20).any(1)
crossing_times=(np.abs(walks[hit20])>=20).argmax(1)
print(walks.max(1))
print(walks.max())
print(crossing_times)