牛客 动物森友会（最大流+二分）

链接：https://ac.nowcoder.com/acm/problem/205306
来源：牛客网

Compute 最近开始玩动物森友会了。
这个游戏的时间与现实时间是同步的（一周有 7 天），而一些特定事件只会在一周的某些天解锁。
我们假设有 n个不同的事件，而每个事件都会给予不同的材料，并且每个事件只会在一周中的特定几天开放，在开放的时间内可以完成多次。但由于 Compute 要参加训练，他每天并没有多少时间玩游戏，所以他每天最多只能完成 e次事件。
现在 Compute 想做出一件非常稀有的道具——高达，并且他计算出了他收集齐所有材料需要完成每一种事件的次数。
假设现在 Compute 从周一开始玩这个游戏，他最少需要经过几天（包括不玩游戏的日子）才能造出高达？

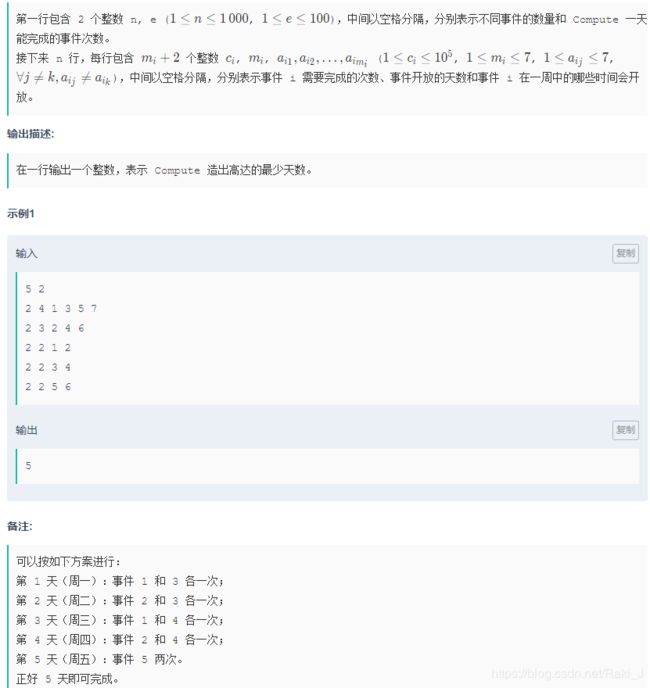
每天可做的事件数量为e，一周有七天 ，有n个不同的事件，在不同的日子开放，每件事要完成c次，求最少多少天能达成，可以看出来是最大流，并且要求最少日子，故配合二分答案食用
思路是先记录每个事件要完成的次数，事件i在day x 是否开放
然后二分最少需要的天数，check的过程中建图并求出最大流
如果最大流==c的总和 代表这么多日子够造出高达（因为事件到汇点的容量限制，不会超过总和）
建图的思路：对每天，ee代表一天能完成任务的数量，
mid为二分答案过程中当前的天数，从源点到每天建立一条 容量为（mid/7）乘ee的边
如果%7有余数就多加一份ee

for(int i=1;i<=7;i++){
        if(mid%7>=i){
            add_edge(s,i+s,(mid/7)*ee+ee);
            add_edge(i+s,s,0);
        }
        else{
            add_edge(s,i+s,(mid/7)*ee);
            add_edge(i+s,s,0);
        }
    }

每天对相应的事件建一条容量为inf的边

每个事件到汇点建立一条容量为c的边（需要完成的次数）

for(int i=1;i<=n;i++){
        add_edge(7+i+s,t,c[i]);
        add_edge(t,7+i+s,0);
        for(int j=1;j<=7;j++){
            if(g[i][j]==1){
                add_edge(j+s,7+i+s,inf);
                add_edge(7+i+s,j+s,0);
            }
        }
    }

然后就可以写出完整代码了，撒花~

#include
using namespace std;
const int inf =0x3f3f3f3f,maxn=1e5+5,maxm=4e5+5;
int cur[maxn],head[maxn],dep[maxn];
int cnt=1,n,s,t,ee;
int c[maxn],m[maxn],g[maxn][10],sum;
struct edge{
    int v,w,nex;
}e[maxm*2];
inline void add_edge(int u,int v,int w){
    e[++cnt].v=v;
    e[cnt].w=w;
    e[cnt].nex=head[u];
    head[u]=cnt;
}
bool bfs(){
    memset(dep,0,sizeof(dep));
    for(int i=1;i<=n+10;i++){
        cur[i]=head[i];
    }
    dep[s]=1;
    queue<int>q;
    q.push(s);
    while(!q.empty()){
        int u=q.front();
        q.pop();
        for(int i=head[u];i;i=e[i].nex){
            int v=e[i].v;
            if(!dep[v]&&e[i].w){
                dep[v]=dep[u]+1;
                q.push(v);
                if(v==t)return true;       
            }
        }
    }
    return false;
}
int dfs(int u,int now){
    if(u==t||now==0){
        return now;
    }
    int flow=0,rlow=0;
    for(int i=cur[u];i;i=e[i].nex){
        int v=e[i].v;
        if(e[i].w&&dep[v]==dep[u]+1){
            if(rlow=dfs(v,min(now,e[i].w))){
                flow+=rlow;
                now-=rlow;
                e[i].w-=rlow;
                e[i^1].w+=rlow;
                if(now==0)return flow;
            }
        }
    }
    if(!flow)dep[u]=-1;
    return flow;
}
int dinic(){
    int maxflow=0;
    while(bfs()){
        maxflow+=dfs(s,inf);
    }
    return maxflow;
}
bool check(int mid){
    memset(head,0,sizeof(head));
    cnt=1;
    for(int i=1;i<=7;i++){
        if(mid%7>=i){
            add_edge(s,i+s,(mid/7)*ee+ee);
            add_edge(i+s,s,0);
        }
        else{
            add_edge(s,i+s,(mid/7)*ee);
            add_edge(i+s,s,0);
        }
    }
    for(int i=1;i<=n;i++){
        add_edge(7+i+s,t,c[i]);
        add_edge(t,7+i+s,0);
        for(int j=1;j<=7;j++){
            if(g[i][j]==1){
                add_edge(j+s,7+i+s,inf);
                add_edge(7+i+s,j+s,0);
            }
        }
    }
    int mf=dinic();
    if(mf>=sum)return true;
    else return false;
}
int main(){
    scanf("%d%d",&n,&ee);
    s=1,t=7+n+2;
    sum=0;
    for(int i=1;i<=n;i++){
        scanf("%d%d",&c[i],&m[i]);
        sum+=c[i];
        for(int j=1,d;j<=m[i];j++)scanf("%d",&d),g[i][d]=1;
    }
    int l=1,r=(sum/ee+1)*7+100;
    int ans=0;
    while(l<=r){
        int mid=(l+r)>>1;
        if(check(mid)){
            ans=mid;
            r=mid-1;
        }
        else{
            l=mid+1;
        }
    }
    printf("%d\n",ans);
    return 0;
}