学习机器学习三 分类模型 k-NN算法

我们接着上一篇继续学习，还是在监督学习的范围内。先讲一下机器学习中最简单的算法之一——k-NN算法。什么是k-NN算法作者举了一个例子，我“填油加醋”的转述下。

假如：湖人队球迷讨厌凯尔特人队球迷，并且不愿与他们做邻居，你搬来我就搬走的地步。凯尔特人队球迷也不喜欢湖人队球迷，不想跟他们做邻居。这时候有个公司在促销凯尔特人队的宣传物品，刚开始一家家敲门推销宣传，可是如果是湖人队球迷它们就会被赶走，那么他们怎么知道哪些家庭可能是湖人队球迷家庭呢？

这就是k-NN算法要做的事了——简单来说，k-NN算法认为一个数据点很可能与它近邻的点属于同一个类别。也就是我们说的湖人队球迷家庭附近往往不会存在凯尔特人队球迷家庭。如果情况更为之复杂（数据点更为混乱密集）呢，这个时候我们就不会只考虑最邻近类别（k=1）了，而是考虑k=n个最邻近的类别。就是说考虑的不再是最邻近的一个点是什么类，我们就认为它是什么类。而是考虑最邻近的k个点，大部分是什么类，我们才归为它是那个类。

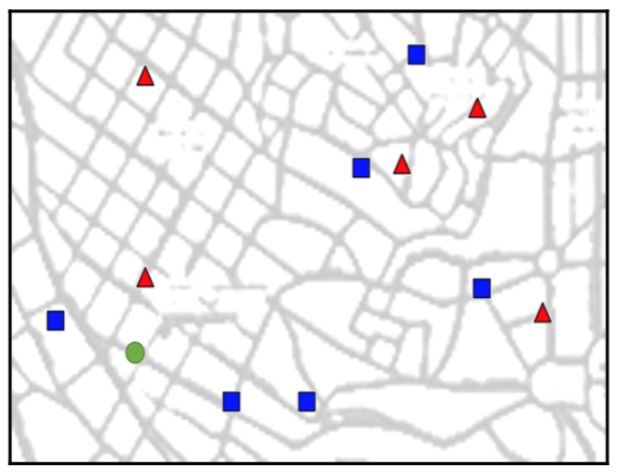
首先他把之前去过的家庭位置收集成数据，三角形的是湖人队人，正方形是凯尔特人队，圆圈是他要预测的家庭：

k-NN算法也包含在了Opencv中，那么实现它只需要以下几步：

①生成一些训练数据

②指定k值，创建一个k-NN对象

③找到想要分类的新数据点的k个最邻近的点

④使用多数投票来分配新数据点的类标签

⑤画出结果图

 

过滤一下实现代码是我最喜欢做的事啦：

import numpy as np
import cv2
import matplotlib.pyplot as plt

# 如果用Jupyter，定义这个就不用每次show（）了
%matplotlib inline

# 老规矩让每次数据都固定不变
np.random.seed(42)

# 随机生成一个点叫被预测点，范围在0-99，其实就是生成0-99范围内2个数，我们人为看成点(x,y)
single_data_point = np.random.randint(0, 100, 2)  #输出array([51, 92])

# 随机生成一个数0-1之间，假设这是上述那个被预测点所属的类别
single_label = np.random.randint(0, 2)  #输出0

# 包装一个函数，随机生成多个数据点
def generate_data(num_samples, num_features=2):

    # 决定要生成多少个训练数据点
    data_size = (num_samples, num_features)

    # 生成X维Y列矩阵，每一个维度都是一个数据点，这是一个地图，所以x,y代表一个点
    train_data = np.random.randint(0, 100, size=data_size)

    # 给每个样本创建一个标签
    labels_size = (num_samples, 1)
    labels = np.random.randint(0, 2, size=labels_size)
    
    # 返回生成的数据
    return train_data.astype(np.float32), labels

# 函数调用，生成训练数据
train_data, labels = generate_data(11)
#输出train_data为
array([[ 71.,  60.],
       [ 20.,  82.],
       [ 86.,  74.],
       [ 74.,  87.],
       [ 99.,  23.],
       [  2.,  21.],
       [ 52.,   1.],
       [ 87.,  29.],
       [ 37.,   1.],
       [ 63.,  59.],
       [ 20.,  32.]], dtype=float32)
#输出labels 为
array([[ 1],
       [ 1],
       [ 0],
       [ 1],
       [ 0],
       [ 0],
       [ 0],
       [ 1],
       [ 1],
       [ 0],
       [ 1]], dtype=float32)

# 抽一个点看下它是什么类
train_data[0], labels[0]  #输出labels 为(array([ 71.,  60.], dtype=float32), array([1]))

# 现在我们把我们生成的数据点画出来
# 要注意下写法train_data[0, 0]代表71，train_data[0, 1]代表60,不要写成train_data[0]
plt.plot(train_data[0, 0], train_data[0, 1], 'sb')  

plt.xlabel('x coordinate')
plt.ylabel('y coordinate')

结果图：

# 那样一个个显示太慢了，我们包装一个函数一次把数据点都画出来，还要加点样式装饰下
def plot_data(all_blue, all_red):
    plt.figure(figsize=(10, 6))
     
    # 这里all_blue[:, 0]代表蓝色的所有X点，all_blue[:, 1]代表蓝色的所有y点
    plt.scatter(all_blue[:, 0], all_blue[:, 1], c='b', marker='s', s=180)

    # 这里all_red[:, 0]代表红色的所有X点，all_red[:, 1]代表红色的所有y点
    plt.scatter(all_red[:, 0], all_red[:, 1], c='r', marker='^', s=180)

    plt.xlabel('x coordinate (feature 1)')
    plt.ylabel('y coordinate (feature 2)')

# 找出标签为0的数据点，就是蓝色的数据点
labels.ravel() == 0  #输出array([False, False, False,  True, False,  True,  True,  True,  
                     True,True, False], dtype=bool)

blue = train_data[labels.ravel() == 0]
red = train_data[labels.ravel() == 1]
plot_data(blue, red)

结果图：

总结下这个做法，值得注意的一点是，X,Y我们要分开，思想上当成point，编码上不要当成point，它是数组的每一个维度列值而不是点。我觉得要想学好机器学习，记住常用的函数是很重要的。

接着我们的操作，现在是训练分类器的时候了，和其它所有的机器学习函数一样，可以用OpenCV来创建一个分类器：

knn = cv2.ml.KNearest_create()

然后把训练数据传入train中：

knn.train(train_data, cv2.ml.ROW_SAMPLE, labels)  #输出True

现在预测新数据点的类别，k-NN提供了一个叫做findNearest的方法，它是根据最近的数据点标签来预测新数据点的标签，我们之前已经生成一个被预测数据点了，可以把它当成只有一个数据的测试数据集：

newcomer, _ = generate_data(1)  #输出array([[ 91.,  59.]], dtype=float32)

# 把我们需要预测的点也画出来，因为刚才关了，所以再把之前的画出来
plot_data(blue, red)

# 然后添加新画的点
plt.plot(newcomer[0, 0], newcomer[0, 1], 'go', markersize=14);

# 找出最邻近的一个点
ret, results, neighbor, dist = knn.findNearest(newcomer, 1)
print("Predicted label:\t", results)
print("Neighbor's label:\t", neighbor)
print("Distance to neighbor:\t", dist)
#输出Predicted label:	 [[ 1.]]
Neighbor's label:	 [[ 1.]]
Distance to neighbor:	 [[ 250.]]
# 这告诉我们最邻近的点类别是1，距离有250这么远，因此新的数据点应该是属于标签1

# 找出最邻近的七个点试试，会不会影响它的预测结果
ret, results, neighbor, dist = knn.findNearest(newcomer, 7)
print("Predicted label:\t", results)
print("Neighbor's label:\t", neighbor)
print("Distance to neighbor:\t", dist)
#输出Predicted label:	 [[ 0.]]
Neighbor's label:	 [[ 1.  1.  0.  0.  0.  1.  0.]]
Distance to neighbor:	 [[  250.   401.   784.   916.  1073.  1360.  4885.]]
# 这告诉我们最邻近的7点类别是[ 1.  1.  0.  0.  0.  1.  0.],因此新的数据点应该是属于标签0

到这里我们利用k-NN来预测这户人家是湖人队球迷还是凯尔特人队球迷就已经结束了。说到正题，我们可以明显的看到随着k值的变化，我们的预测结果也发生改变，所以通过尝试不同的k值，才能得到最合适我们的分类器。我觉得我说的非常的详细、简单和明了。

这些学习笔记是我在拜读了Michael Beyeler著的《机器学习 使用OpenCV和Python进行智能图像处理》的自我理解，感谢。