
凌云时刻 · 技术


导读:上一节中,我们讲了使用多项式的方式使得逻辑回归可以解决非线性分类的问题,那么既然使用了多项式方法,那势必模型就会变的很复杂,继而产生过拟合的问题。所以和多项式解决回归问题一样,在逻辑回归中使用多项式也要使用模型正则化来避免过拟合的问题。
作者 | 计缘
来源 | 凌云时刻(微信号:linuxpk)
逻辑回归中使用模型正则化

这一节我们使用Scikit Learn中提供的逻辑回归来看一下如何使用模型正则化。在这之前先来复习一下模型正则化。所谓模型正则化,就是在损失函数中加一个带有系数的正则模型,那么此时如果想让损失函数尽可能的小,就要兼顾原始损失函数和正则模型中的 值,从而做以权衡,起到约束多项式系数大小的作用。正则模型前的系数 决定了新的损失函数中每一个 都尽可能的小,这个小的程度占整个优化损失函数的多少。
范数请参见机器学习笔记九之交叉验证、模型正则化 。
但是这种方式有一个问题,那就是可以刻意回避模型正则化,也就是将 取值为0的时候。所以还有另一种模型正则化的方式是将这个系数加在原始损失函数前面,这种情况的话相当于正则模型前的系数永远是1,无论如何都要进行模型正则化。
Scikit Learn中的逻辑回归就自带这种形式的模型正则化,下面我们来看一下:
import numpy as np
import matplotlib.pyplot as plt
# 构建样本数据,构建200行2列的矩阵,均值为0,标准差为1,既200个样本,每个样本2个特征
X = np.random.normal(0, 1, size=(200, 2))
# 构建y的方程,曲线为抛物线
y = np.array(X[:, 0]**2 + X[:, 1] <1.5, dtype='int')
# 在样本数据中加一些噪音
for _ in range(20):
y[np.random.randint(200)] = 1
# 绘样本数据
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()
|

样本数据构建好了,我们先用逻辑回归对其进行分类预测看看准确度:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y)
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
# 结果
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
penalty='l2', random_state=None, solver='liblinear', tol=0.0001,
verbose=0, warm_start=False)
|
当模型训练完后,我们在返回内容中可以看到两个超参数C和penalty,前者就是前面讲到的原始损失函数前的系数,后者就是正则模型,逻辑回归中这两个超参数的默认值是1和 范式正则模型,也就是LASSO正则模型。
log_reg.score(X_test, y_test)
# 结果
0.80000000000000004
# 绘制决策边界
plot_decision_boundary(log_reg, axis=[-3, 3, -3, 3])
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()
|
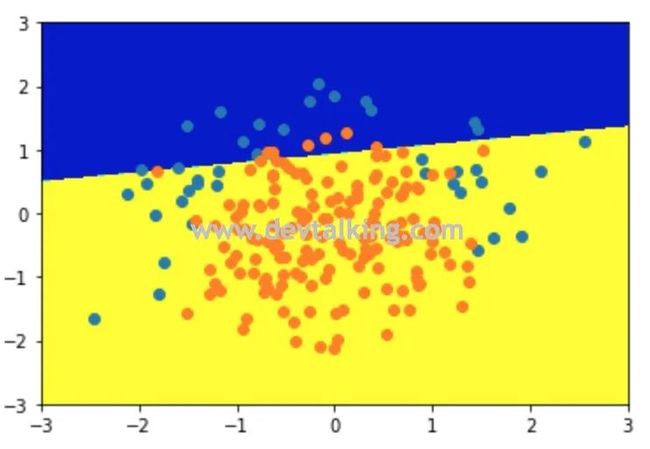
可以看到用线性逻辑回归训练出的模型准确度只有80%,并且线性决策边界无法很好的区分两种分类。下面我们再用多项式逻辑回归训练模型看看:
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
def PolynomialLogisiticRegression(degree, C):
return Pipeline([
('poly', PolynomialFeatures(degree=degree)),
('std_scaler', StandardScaler()),
('log_reg', LogisticRegression(C=C))
])
ploy_log_reg = PolynomialLogisiticRegression(degree=2, C=1)
ploy_log_reg.fit(X_train, y_train)
ploy_log_reg.score(X_test, y_test)
# 结果
0.93999999999999995
plot_decision_boundary(ploy_log_reg, axis=[-3, 3, -3, 3])
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()
|

可以看到当使用多项式逻辑回归后,模型准确度达到了94%,不规则决策边界也很好的区分了两种类型。下面我们增加多项式的复杂度,再来看看:
ploy_log_reg2 = PolynomialLogisiticRegression(degree=20, C=1)
ploy_log_reg2.fit(X_train, y_train)
ploy_log_reg2.score(X_test, y_test)
|
可以看到当degree增大到20时,模型准确率有所下降,因为我们的样本数据量比较小,所以过拟合的现象不是很明显,我们绘制出决策边界看看:
plot_decision_boundary(ploy_log_reg2, axis=[-3, 3, -3, 3])
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()
|
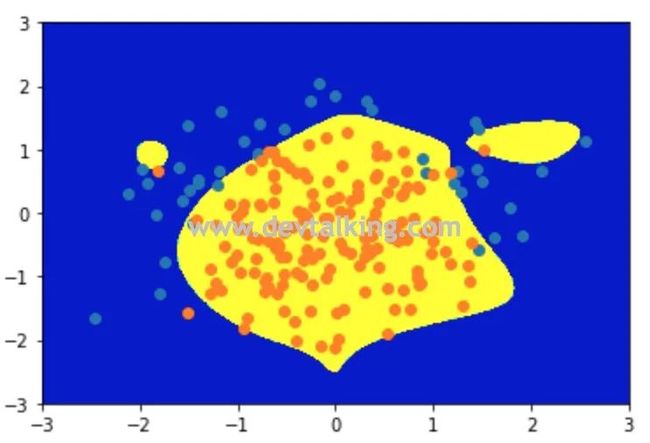
从决策边界上能很明显的看到过拟合的状态。下面我们来调整C这个系数,让正则模型来干预整个损失函数中 的大小,然后再看看模型准确率和决策边界:
ploy_log_reg3 = PolynomialLogisiticRegression(degree=20, C=0.1)
ploy_log_reg3.fit(X_train, y_train)
ploy_log_reg3.score(X_test, y_test)
# 结果
0.92000000000000004
plot_decision_boundary(ploy_log_reg3, axis=[-3, 3, -3, 3])
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()
|
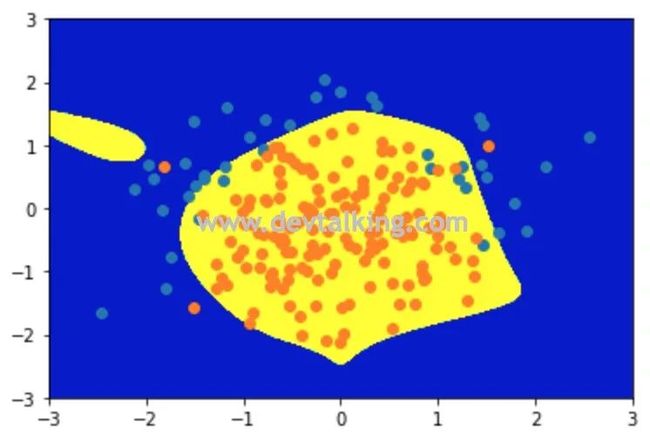
可以看到当正则模型进行干预后,模型的准确率有所提升,决策边界也比之前好了许多。这就是逻辑回归中的模型正则化。
逻辑回归解决多分类问题

在前面的章节中,对逻辑回归的应用一直是在二分类问题中进行的。这一节来讲讲能够让逻辑回归解决多分类问题的方法。
 OvR
OvR
所谓OvR就是One vs Rest的缩写,从字面上来讲是一对剩余的所有的意思。那么我们通过一系列示图来解释一下OvR:

假设有四个分类,如上图所示,如果One指的是蓝色的点,那么剩余的红色、绿色、黄色三个点就是Rest,也就是我们选取一个类别,把其他剩余的类别称之为剩余类别:

这样就把一个四分类问题转换成了二分类问题,现在我们就可以使用逻辑回归算法预测再来一个点时它属于蓝色点的概率和属于剩余点的概率。
同理,这个过程也可以在其他颜色的点上进行,如果是上图的四分类问题,那么就可以拆分为四个二分类问题:

然后对新来的点分别在这四个二分类问题中计算概率,也就是N个类别就进行N次分类,最后选择分类概率最高的那个二分类,这样就可以判断这个新点的类别了。
 OvO
OvO
所谓OvO就是One vs One的缩写,从字面上来讲是一对一的意思。那么我们同样通过一系列示图来解释一下OvO:

还是假设有四个分类,将其中的每两个分类单独拿出来处理,这样就一共有六组二分类问题,然后对新来的点分别在这六个二分类问题中计算概率,最后选择分类概率最高的那个二分类,这样就可以判断这个新点的类别了,这就是OvO方式。很明显OvO方式的时间复杂度要比OvR高很多,但是准确率也高很多,因为每次都是在绝对的二分类中对新来的样本数据进行概率计算
 Scikit Learn中的逻辑回归
Scikit Learn中的逻辑回归
这一节我们来看看Scikit Learn中封装的逻辑回归。我们使用鸢尾花的样本数据:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
# 结果
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
penalty='l2', random_state=None, solver='liblinear', tol=0.0001,
verbose=0, warm_start=False)
log_reg.score(X_test, y_test)
# 结果
0.94736842105263153
|
从打印结果中我们能看到有一个属性叫multi_class它的值为ovr,其实Scikit Learn中的逻辑回归是自带OvR和OvO能力的,默认使用OvR。另外还需要注意solver属性,这个属性指定了逻辑回归使用的算法,如果使用了ovr,则对应的算法是liblinear。
log_reg1 = LogisticRegression(multi_class='multinomial', solver='newton-cg')
log_reg1.fit(X_train, y_train)
log_reg1.score(X_train, y_train)
# 结果
0.9732142857142857
|
如果要使用OvO方式,需要显示的传入multi_class和solver这两个参数,对应OvO的算法是newton_cg,这里就不对这两个算法做详细解释了,可以看看Scikit Learn的官网说明。
 OvO和OvR类
OvO和OvR类
除了在逻辑回归中自带了OvR和OvO方式以外,Scikit Learn还专门提供了单独的OvR和OvO的类,只要传入一个二分类器,就可以运用OvR和OvO的原理来解决多分类问题了:
from sklearn.multiclass import OneVsRestClassifier
ovr = OneVsRestClassifier(log_reg)
ovr.fit(X_train, y_train)
ovr.score(X_test, y_test)
# 结果
0.94736842105263153
from sklearn.multiclass import OneVsOneClassifier
ovo = OneVsOneClassifier(log_reg)
ovo.fit(X_train, y_train)
ovo.score(X_test, y_test)
# 结果
1.0
|
总结

这两篇笔记主要讲了逻辑回归,这是解决分类问题应用很广泛的一个算法,它拓展了线性回归算法,将估算概率的方式将回归问题转换为了分类问题。下一篇笔记将讨论如何更好的评价分类问题的准确度。
END

往期精彩文章回顾

机器学习笔记(二十一):决策边界
机器学习笔记(二十):逻辑回归(2)
机器学习笔记(十九):逻辑回归
机器学习笔记(十八):模型正则化
机器学习笔记(十七):交叉验证
机器学习笔记(十六):多项式回归、拟合程度、模型泛化
机器学习笔记(十五):人脸识别
机器学习笔记(十四):主成分分析法(PCA)(2)
机器学习笔记(十三):主成分分析法(PCA)
机器学习笔记(十二):随机梯度下降

长按扫描二维码关注凌云时刻
每日收获前沿技术与科技洞见
![]()
![]()
![]()
![]()
![]()
![]() OvR
OvR OvO
OvO![]() Scikit Learn中的逻辑回归
Scikit Learn中的逻辑回归![]() OvO和OvR类
OvO和OvR类![]()
![]()
![]()








