利用Breadth-First Search (BFS)算法寻找图中的最短路径和所有路径

       今天在stackoverflow网站搜索问题时，发现了一个用BFS算法搜索图中最短路径比较简洁且容易理解的代码。暂且放在博客记录下来，方便今后用到。

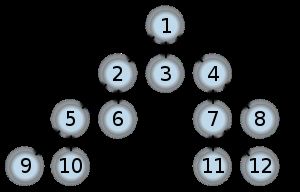
      如上图，我们要使用BFS算法搜索1—11的最短路径，代码如下：

 

# graph is in adjacent list representation
graph = {
        '1': ['2', '3', '4'],
        '2': ['5', '6'],
        '5': ['9', '10'],
        '4': ['7', '8'],
        '7': ['11', '12']
        }

def bfs(graph, start, end):
    # maintain a queue of paths
    queue = []
    # push the first path into the queue
    queue.append([start])
    while queue:
        # get the first path from the queue
        path = queue.pop(0)
        # get the last node from the path
        node = path[-1]
        # path found
        if node == end:
            return path
        # enumerate all adjacent nodes, construct a new path and push it into the queue
        for adjacent in graph.get(node, []):
            new_path = list(path)
            new_path.append(adjacent)
            queue.append(new_path)

print bfs(graph, '1', '11')

输出结果：[1，4，7，11]

 

      如果我们修改几个地方，增加了节点3的临节点，网络拓扑已改变。则可以得到源和目的节点的所有路径，代码如下：

 

# graph is in adjacent list representation
graph = {
        1: [2, 3, 4],
        2: [5, 6],
        3: [4,11],
        5: [9, 10],
        4: [7, 8],
        7: [11, 12]
        }

def bfs(graph, start, end):
    # maintain a queue of paths
    queue = []
    allpath = []
    # push the first path into the queue
    queue.append([start])
    while queue:
        # get the first path from the queue
        path = queue.pop(0)
        # get the last node from the path
        node = path[-1]
        # path found
        if node == end:
            allpath.append(path)
        # enumerate all adjacent nodes, construct a new path and push it into the queue
        for adjacent in graph.get(node, []):
            new_path = list(path)
            new_path.append(adjacent)
            queue.append(new_path)
    return allpath

print bfs(graph, 1, 11)

 

输出结果：[[1, 3, 11], [1, 4, 7, 11], [1, 3, 4, 7, 11]]

2019年补充： 

后来看到有人开发了一个用于复杂网络的Python包——networkx，这个包里面有很多的路径算法我们可以直接用，其原理是用改进的DFS等。

求解图G中source到target的所有简单路径：netwrkx.all_simple_paths(G, source, target, cutoff=None)，复杂度很高，为O(n!)。如果路径较多的，建议设置cutoff，或使用KSP、动态规划等其他方法。

求解图G中source到target的所有最短路径：netwrkx.all_shortest_paths(G, source, target, weight=None)