leetcode实战—素数（埃拉托色尼筛选法包括证明、哈希、RSA）

前言

素数这个概念人类已经研究了上千年，但是的具体的起源却不得而知。早在公元前300年，欧几里得就在他的著作元素中证明了有无穷多个素数，同时也证明了任何一个整数都能够被某一个素数整除。时至今日，素数在计算机科学这样一个和数学联系紧密的学科中也有这个广泛的应用，比如布隆过滤器、伪随机数、RSA加密算法等等，所以掌握素数的特性以及应用能够帮助我们解决不少实际问题。

简介

素数（又称质数）是一个只能被1和它自己整除的整数，换句话说他只有两个因数——1和它自己。比如3是一个素数，因为3只能被1和3整除，但是6不是素数因为它能被2和3整除。迄今为止发现的最大的素数是$2^{57885161}-1$，由中央密苏里大学的数学家Curtis Cooper发现，大概有17,425,170位数字。

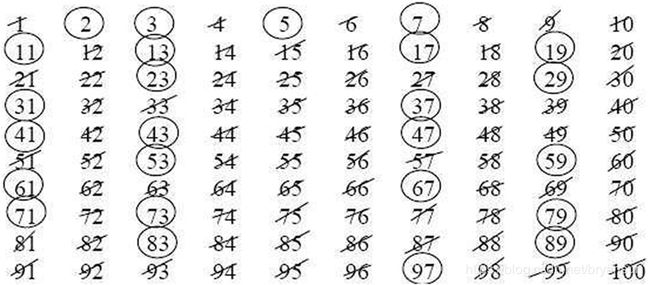
在公元前200年，古希腊数学家埃拉托色尼（Eratosthenes）创造了一套算法用来计算素数，这就是大家熟知的埃拉托色尼筛选法（the Sieve of Eratosthenes），这是最早的用来计算素数的方法。就拿100以内素数的方法来简单介绍一下这个筛选法：

首先我们找到第一个素数2，用圆圈标出来，然后划掉所有2的倍数4、6、8等等。然后我们找到下一个没有被划掉的数字（这个数字肯定不是前面更小数字的倍数），也就是3，用圆圈标出来，再划掉所有的3的倍数，注意这里6已经被划掉了，但是9可以继续被划掉。接下来再用圆圈标出下一个没有被划掉的数字5，划掉所有的5的倍数。如此往复，直到100的平方根10截止，所有的100以内的素数就都被圆圈圈起来了。

计数质数

来看看素数计算的最简单的版本，Leetcode第204题计数质数。

统计所有小于非负整数 n 的质数的数量。

示例：

输入: 10
输出: 4
解释: 小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。

这道题通过我们在上面介绍的埃拉托色尼筛选法可以很轻松的做出来，只需要创建一个小于n的数组，从索引2开始一直到Math.sqrt(n)对整个队列进行筛选，最后统计一遍整个数组里面所有的素数就行了。

public int countPrimes(int n) {
    if (n <= 2) return 0;
    boolean[] primes = new boolean[n];  //创建整个素数数组
    Arrays.fill(primes, true);      //初始化全部位素数
    primes[0] = false;
    primes[1] = false;                  //划掉0和1
    int sqrt = (int)Math.sqrt(n);       //设置上界
    for (int i = 2; i <= sqrt; i++) {
        if (!primes[i]) continue;       //不是素数，可以跳过
        for (int multi = i<<1; multi < n ; multi += i){
            primes[multi] = false;      //划掉倍数
        }
    }
    int count = 0;
    for (boolean prime : primes) {      //统计数组中素数的数量
        if (prime) count++;
    }
    return count;
}

运行了上面的代码之后，执行时间17ms，才击败了60%的用户，代码还有很大的优化空间。我们从上一个小节的筛选法中就可以看到，我们经常要划掉已经被划掉的数字，比如在划掉了所有的2的倍数6之后，我们在划掉3的倍数的时候又划掉了6一次，这样就浪费了我们的资源，能不能直接跳过6去划掉9呢？所以这里就是需要考虑要从哪个数字开始划数字。在划掉2的倍数的时候，我们是划掉2x2、2x3、2x4、2x5等等，在划掉3的时候是划掉3x2（在素数2的那一轮已经被划掉了）、3x3、3x4、3x5等，在划掉5的时候是划掉5x2（素数2的一轮已经被划掉了）、5x3（素数3的一轮被划掉了）、5x4（等于10x2也在素数2的一轮被划掉了）、5x5等等。现在这个规律应该十分明显了，在划掉素数i的倍数的时候，所有比i小的数字的和i的乘积已经被划掉了，所以下一轮直接从i*i开始就行了，于是我们可以把上面代码里面的multi初始化为i*i，代码我就不贴出来了。

其实这道题还有挺多的改进方法的，比如使用BitSet来代替boolean的数组、用false代表是位置i是质数来缩短数组的初始化时间或者在第一个for循环里面就统计所有非质数省去最后一个循环，可以用很多方法减少冗余操作的时间，不过整体最终的时间复杂度是$O(NloglogN)$，第一个for循环是不可避免的，下面我们来用一些数学知识来解释一下这个时间复杂度。

首先我们有数字n代表素数的上边界（不包含），p代表小于n的最大素数，内部循环设置false的时间是恒定的。

当i==2时，内部的筛除操作进行了$\frac{n}{2}$次

当i==3时，筛除了$\frac{n}{3}$次

当i==4时，直接跳过，筛除了$0$次（所有的非素数都会跳过）

当i==5时，筛除了$\frac{n}{5}$次

当i==p时，筛除了$\frac{n}{p}$次

所以总体的运行时间可以看作：

$$\frac{n}{2}+\frac{n}{3}+\frac{n}{5}+...\frac{n}{p}$$

等效于

$$n\times (\frac{1}{2}+\frac{1}{3}+\frac{1}{5}+...\frac{1}{p})$$

现在就是要证明

$$\frac{1}{2}+\frac{1}{3}+\frac{1}{5}+...\frac{1}{p}=loglogn$$

在进行下面的证明的时候，我们需要用到调和级数、泰勒级数、欧拉乘积公式，这几个公式的证明过程感兴趣的可以自己去看看（在我的参考文档里面，纯数学部分，比写代码难多了），就先说我们要用到的定理。

---

调和级数（Harmonic series）是一个发散的无穷级数，当$n$趋近于无穷大时，有一个近似公式：

$$1+\frac{1}{2}+\frac{1}{3}+...=\sum _{i=1}^n\frac{1}{i}=ln(n)+\gamma$$

其中$\gamma$为欧拉常数，$\gamma \approx 0.57721$

---

泰勒级数（Taylor series）是1715年英国数学家布鲁克·泰勒提出的，在零点的导数求得的泰勒级数又叫麦克劳林级数，具体的原版的公式我就不在这里贴出来了，这里只贴一个常用的泰勒级数，也就是以$e$为底数的自然对数的麦克劳林序列

$$ln(1-x)=-\sum _{n=1}^{\infty }\frac{x^n}{n}=-x-\frac{x^2}{2}-\frac{x^3}{3}-..-\frac{x^n}{n}$$

对任意属于$[-1,1)$内的$x$都成立。左右的符号同时取反，可以得到：

$$ln(1-x{)}^{-1}=\sum _{n=1}^{\infty }\frac{x^n}{n}=x+\frac{x^2}{2}+\frac{x^3}{3}+..+\frac{x^n}{n}$$

---

欧拉乘积公式（Euler product）是著名的瑞士数学家欧拉于1737年在俄罗斯的圣彼得堡科学院发表的重要公式，为数学家研究素数的分布奠定了基础，即：

$$\sum _n{n}^{-s}=\prod _p^1(1-p^{-s}{)}^{-1}$$

其中n为自然数，p为素数。

---

继续我们的推理。

在欧拉公式中，我们如果将所有的$s$用$1$来代替就可以得到

$$\sum _n{n}^{-1}=\prod _p^1(1-p^{-1}{)}^{-1}$$

对两侧同时使用$log$函数可以得到

$$ln(\sum _n{n}^{-1})=ln(\prod _p^1(1-p^{-1}{)}^{-1})$$

简化之后可以得到

$$ln(\sum _n{n}^{-1})=\sum _{p}ln((1-p^{-1}{)}^{-1})$$

因为$-1<p^{-1}<1$，所以可以对上面公式的右侧的每一项进行泰勒展开得到

$$ln((1-p^{-1}{)}^{-1})=\sum _{n=1}^{\infty }\frac{1}{n{p}^n}$$

当$p$趋近于无穷大的时候，右侧的公式收敛于$\frac{1}{p}$，就可以得到

$$ln((1-p^{-1}{)}^{-1})=\frac{1}{p}$$

代入到原公式可以得到

$$ln(\sum _n{n}^{-1})=\sum _p\frac{1}{p}$$

上述公式左侧log内部正好是调和级数，把调和级数的近似公式代入左侧可以得到

$$\sum _p\frac{1}{p}=ln(ln(n)+\gamma )$$

忽略右边的常数$\gamma$就可以得到最后的时间复杂度为$O(nln(ln(n)))$，也就是$O(nloglogn)$级别。

除了这个证明过程之外，在数论里面已经有一个定理证明这个时间复杂度——Mertens’ second theorem（维基百科需要科学上网，中文材料好像特别少）。

能够看到这个地方已经说明你有着超人般的毅力（还有什么比数学更令人头疼），如果觉得上面的讲解还不够清楚或者有很多数学的细节不太理解，可以看看参考文档。据我在网上查到的，还没有任何一篇文章能够像这篇一样把埃拉托色尼筛选法的时间复杂度讲的这么清楚的，希望能够帮助到大家。

应用1 哈希算法

哈希表是我们日常开发中用的非常多的一种数据结构，在执行搜索、插入或者删除的时候能够在O(i)的时间内完成操作，相比于二分搜索树最快也要O(logN)的时间，性能得到极大的提高。

哈希表是利用哈希算法将键转化成数组中的一个索引，直接使用这个索引地址找到或者插入元素。常用的哈希算法是通过取模操作拿到索引。比如在下面的代码中，TABLE_SIZE是数组的大小，得到结果就是数组索引。

private int hash(int key) {
    return key % TABLE_SIZE;
}

但是在上面转化的过程中可能会出现冲突，也就是两个不同的Key通过哈希算法得到同一个索引，比如当key为TABLE_SIZE和2*TABLE_SIZE，取模得到的值都是0，产生冲突，不管是索引往后顺移还是使用链表（或者红黑树）都会降低哈希表的性能。数组的长度越小，需要存储的数值越多，就越容易发生冲突，为了尽量减小冲突，通常对素数取模。

比如说现在有一组比较特殊的键key=[0,3,6...99]，并且hashTable的大小是m=12，因为3是12的因数，所以所有的3的倍数都会被哈希到3的倍数的位置中

[0,15,30...]哈希到0
[3,18,33...]哈希到3
[6,21,36...]哈希到6
[9,24,39...]哈希到9
[12,27,42...]哈希到0

如此类推可知虽然我们表的大小是12，但是所有的数字只哈希到了0,3,6,9四个位置，明显不是我们想要的。如果我们把表的大小换成素数13，那么就不会有这么多的冲突。用素数的最大好处是可以尽量避免把有相同特性的元素（在这里特性是所有的键都能被3整除）放到集中的几个位置中。

虽说用素数取模能够减小冲突，但是前提是所有的键并不是完全随机而是有一定特点的。对于完全随机的输入，即使用素数也不能减少冲突。

应用2 RSA加密算法

RSA（Rivest–Shamir–Adleman）是最早的公钥密码系统之一，被广泛用于安全数据传输。在这样的密码系统中，加密密钥是公共的，而解密密钥却是私密的。在RSA中，这种不对称性是基于对两个大质数乘积进行因式分解的实践困难，即“因式分解问题”。 缩写词RSA由Ron Rivest，Adi Shamir和Leonard Adleman的姓氏的首字母组成，他们于1977年首次公开描述了该算法。Clifford Cocks，在英国情报局政府通信总部（GCHQ）工作的英国数学家。 于1973年开发了一个等效系统，但直到1997年才解密。

RSA算法是用两个大质数以及一个辅助值创建一个公共密钥发布出去。这两个素数必须保密。任何人都可以使用公共密钥对信息进行加密，但是只有知道质数的人才能对邮件进行解码。破解RSA加密被称为RSA问题。如果使用足够大的质数作为密钥，那么当前还没有方法可以使破解RSA加密。RSA算法的可行性证明涉及到了费马定律，这里就不多讲了，这里只是简单讲解一下RSA算法的工作过程。

RSA算法涉及到4个步骤：生成密钥、发布密钥、加密和解密

生成密钥：

1. 随机挑选两个不同的素数$p$和$q$
2. 计算$n=p\ast q$
3. 计算n的卡迈克尔函数值$\lambda (n)$，也就是$p-1$和$q-1$的最小公倍数（least common multiple）
4. 在$1$和$\lambda (n)$之间选取一个和$\lambda (n)$互质的整数$e$（也就是和$\lambda (n)$的最大公倍数是1的整数）
5. 计算$emod\lambda (n)$的一个模逆元$d$，用人话说就是找到$d$使得$(d\ast e)\%(\lambda (n))=1$

公钥由模数$n$和指数$e$组成，私钥由模数$n$和指数$d$组成。$p$$q$和$\lambda (n)$都必须保密，因为他们能用来计算$d$。

使用密钥：

如果B想发送消息给A，B会首先用A的公钥去加密信息，然后把加密的信息传递给A，最后A用自己的密钥去解密密文。对于第三方，如果没有A的密钥就无法解密B的密文，所以这个信息只有A能够看到。

加密过程：

如果B想发送信息$M$给A，首先获得A的公钥$n$和$e$，加密的密文就是

$c=m^{e}modn$

解密过程：

A收到B的信息$c$之后，用自己的密钥$n$和$d$解密

$c^{d}modn=(m^{e}modn{)}^{d}modn=m$

举个例子：

1. 生成密钥首先选取两个质数:$p=61$，$q=53$
2. 计算$n=61\times 53=3233$
3. 计算$\lambda (n)=lcm(60,52)=780$
4. 选取$e=17$
5. 找到模逆元$d=413$，因为$413\times 17=7021‬$，$7021\%780=1$
6. 假设信息为$m=65$，加密的密文为$c=65^{17}mod3233=2790$
7. 收到信息后进行解密，解密信息为$m=2790^{413}mod3233=65$

为什么说这个加密算法很难破解呢？因为在实践中很容易找到符合要求的一组特别大的$e$、$d$和$n$使得所有的小于$n$的整数$m$都能满足

$(m^d{)}^{e}modn=m$

但是如果我们仅仅知道$e$和$n$，凭借现在计算机能够提供的算力却几乎不能计算出$d$（对于特别大的素数的因式分解是一件特别困难的事情），而没有$d$就不能解密信息。所以选取的素数的越大，破解的难度就越大，加密算法就越安全。

总结

这篇文章写着写着就扯远了，从leetcode题目到RSA加密算法。素数个数的计算用到了埃拉托色尼筛选法，时间复杂度为$O(nloglogn)$，空间复杂度为$O(n)$，这篇文章给出了详细的时间复杂度的证明，为了节省篇幅忽略了基础定理的证明。在哈希算法中我们使用素数来尽量减少键的冲突，提高效率。在RSA加密算法中，创作者利用了两个大素数乘积很难进行因式分解的特点以及费马小定律设计了一套加密和解密信息的规则，使RSA成为当今应用最多的非对称加密加密协议。

参考

Prime Numbers–Why are They So Exciting?
prime number
What is a Prime Number?
如何高效判定、筛选素数
LeetCode一求素数算法优化的简单研究
How is the time complexity of Sieve of Eratosthenes is n*log(log(n))?
调和级数近似求和公式推导
欧拉乘积公式的推导过程
泰勒公式
泰勒级数
Prime Numbers in Hash Functions
RSA (cryptosystem)
Why RSA Works: Three Fundamental Questions Answered
EULER AND THE PARTIAL SUMS OF THE PRIME HARMONIC SERIES
Mertens’ theorems

更多内容请看我的个人博客