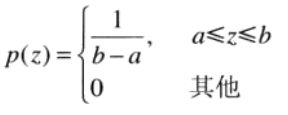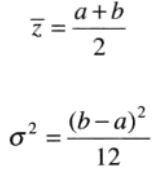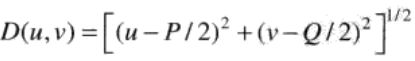数字图像处理——第五章(图像复原与重建)
文章目录
- 一、图像退化与复原
- 1.1 概念
- 1.2 退化/复原过程的模型
- 二、噪声模型
- 2.1 噪声的空间和频率特性
- 2.2 一些重要的噪声概率密度函数(PDF)
- 2.2.1 高斯噪声(电路噪声,由低照明度或高温带来的传感器噪声)
- 2.2.2 瑞利噪声(距离成像噪声)
- 2.2.3 爱尔兰噪声(又称为伽马噪声,是激光成像噪声)
- 2.2.4 指数噪声(激光成像噪声)
- 2.2.5 均匀噪声(仿真中产生随机数)
- 2.2.6 脉冲(椒盐)噪声(成像中的暂态,如错误开关操作)
- 2.3 周期噪声
- 2.4 噪声参数估计
- 三、只存在噪声的复原——空间滤波(去噪复原)
- 3.1 均值滤波器
- 3.1.1 算术均值滤波器
- 3.1.2 几何均值滤波器
- 3.1.3 谐波均值滤波器
- 3.1.4 逆谐波均值滤波器
- 3.2 统计排序滤波器
- 3.2.1 中值滤波器
- 3.2.2 最大值和最小值滤波器
- 3.2.3 中点滤波器
- 3.2.4 修正的阿尔法均值滤波器
- 3.3 自适应滤波器
- 3.3.1 自适应局部降低噪声滤波器
- 3.3.2 自适应中值滤波器
- 四、用频率域滤波消除周期噪声(去噪复原)
- 4.1 带阻滤波器
- 4.2 带通滤波器
- 4.3 陷波滤波器
- 4.4 最佳陷波滤波
- 五、考虑图像退化函数
- 5.1 线性、位置不变的退化
- 5.2 退化函数的估计
- 5.2.1 图像观察估计
- 5.2.2 试验估计
- 5.2.3 建模估计
- 5.3 逆滤波
- 5.4 最小均方误差(维纳)滤波
- 5.5 约束最小二乘方滤波
- 5.6 几何均值滤波
一、图像退化与复原
1.1 概念
退化:成像过程中的“退化”是指由于成像系统各种因素的影响,使得图像质量降低。如,图像的模糊、有外界干扰等。
引起图像退化的原因:
- 成像系统的散焦
- 成像设备与物体的相对运动
- 成像器材的固有缺陷
- 外部干扰等
图像复原:是图像退化的逆过程。以预先确定的目标来改善图像。是一个客观过程。试图利用退化线性的某种先验知识来复原被退化的图像。换句话说,复原的过程为:找图像退化的原因 -> 建立退化模型 -> 反向推演 -> 恢复图像。
- 在图像退化确知的情况下,图像退化的逆过程是有可能进行的
- 实际情况经常是退化过程并不知晓,这种复原称为盲目复原。
1.2 退化/复原过程的模型
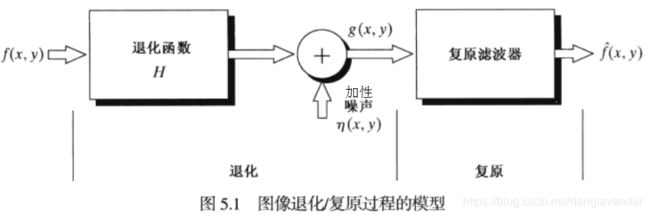
退化过程被建模为一个退化函数和一个加性噪声。给定退化图像g(x,y)和关于退化函数H及加性噪声η(x,y)的一些相关知识后,复原图像就是获得原始图像的一个估计f ̂(x,y)。知道的关于H和η信息越多,f ̂(x,y)就会越接近f(x,y)。
如果H是一个线性的、位置不变的过程。空间域的退化图像如下:
![]()
对应的,频域的退化图像如下:
![]()
二、噪声模型
噪声来源:图像的获取(数字化过程)和传输过程。
噪声分类:根据如何添加进信号中的 可分为加性噪声和乘性噪声。
- 加性噪声:加性噪声一般指热噪声、散弹噪声等,它们与信号的关系是相加,不管有没有信号,噪声都存在。是一种线性变化。
- 乘性噪声:乘性噪声一般由信道不理想引起,它们与信号的关系是相乘,信号在它在,信号不在他也就不在。是一种非线性的变换方式,属于非线性系统。
2.1 噪声的空间和频率特性
空间特性:定义噪声空间特性的参数,及噪声是否与图像相关。
频率特性:傅里叶域中噪声的频率内容(即相对于电磁波谱的频率)。
白噪声:噪声的傅里叶谱是常量。
本章中,假设噪声与空间坐标无关,并且噪声与图像本身不相关(即像素值与噪声成分的值之间不相关,加性噪声)。
2.2 一些重要的噪声概率密度函数(PDF)
2.2.1 高斯噪声(电路噪声,由低照明度或高温带来的传感器噪声)
在空间域和频率域中,高斯噪声在数学上具有易处理性,故实践中常用该噪声模型,以至于高斯模型常用于在一定程度上导致最好结果的场合。
高斯随机变量z的PDF如下:
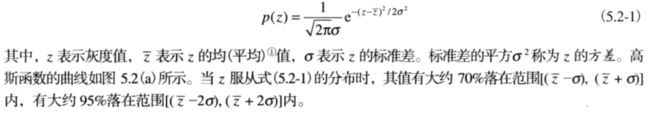
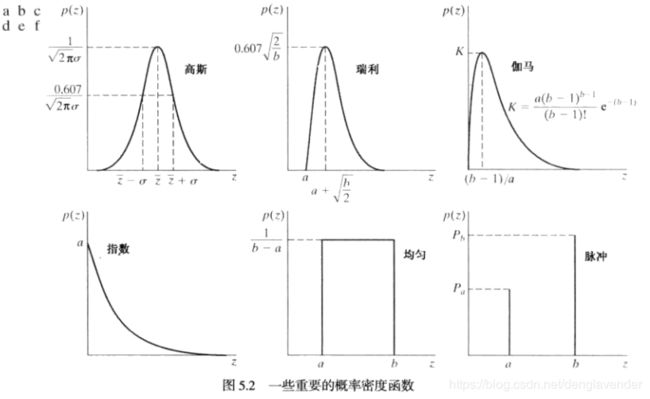
2.2.2 瑞利噪声(距离成像噪声)
瑞利噪声的PDF如下:
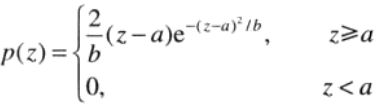
概率密度的均值和方差为:

a为距离原点的距离。密度的基本形状向右变形。瑞利密度对于近似歪斜的直方图十分适用。
2.2.3 爱尔兰噪声(又称为伽马噪声,是激光成像噪声)
伽马噪声的PDF如下:
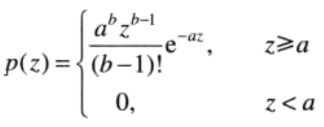
其中,a>0,b为正整数。其概率密度的均值和方差为:
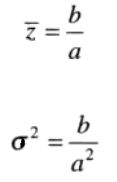
2.2.4 指数噪声(激光成像噪声)
指数噪声的PDF如下:
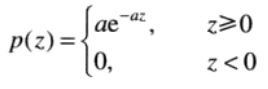
其中a>0。概率密度的均值和方差如下:
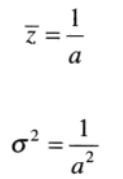
当爱尔兰噪声PDF中的b = 1时,就变成了指数噪声PDF。故指数噪声PDF是爱尔兰噪声PDF的特殊情况。
2.2.5 均匀噪声(仿真中产生随机数)
2.2.6 脉冲(椒盐)噪声(成像中的暂态,如错误开关操作)
(双极)脉冲噪声的PDF如下:
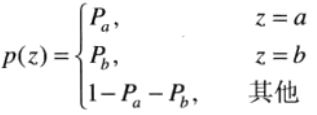
在图像中 b 和 a, 一个是白点,一个是黑点。如果 Pa 或Pb 为零,则脉冲噪声称为单脉冲噪声;如果 Pa 和 Pb 均不为0,且大致相等的时候,脉冲噪声值将类似于在图像上随机分布的胡椒和盐粒,故双极脉冲噪声也称为椒盐噪声。
实际上在椒盐噪声中,噪声的值未必都是图像可取值范围中的最大值和最小值。但是与图像信号的强度相比,脉冲污染通常比较大,所以在一幅图像中脉冲噪声通常被数字化为最大值(纯黑或纯白)。
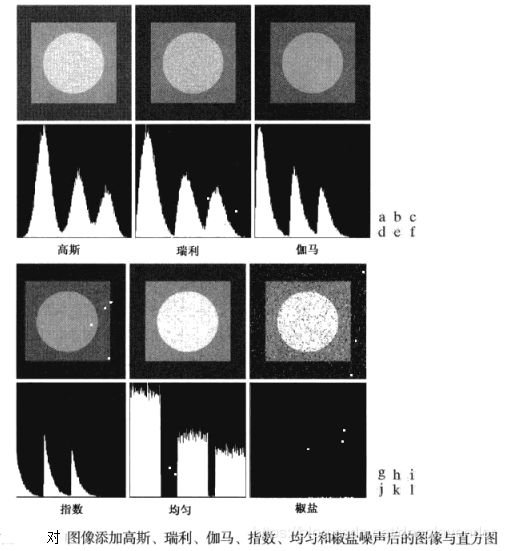
直观来看,前五种噪声很难通被污染的图像本身进行区别,但是椒盐噪声是可以被区分出来的。虽然前五种图像不好区分,但是它们的直方图却很容易区分。所有在后面确定噪声参数的时候,往往首先根据噪声的直方图来确定噪声的种类,再计算该类噪声所对应的参数。
使用函数imnoise对图像添加噪声。基本语法如下:
g=imnoise(f,type,parameters)
f是输入图像,type是噪声类型,parameters指一些参量。函数 imnoise在给图像添加噪声之前,将图像转换为范围 [0,1] 内的double类图像。指定噪声参数时,必须考虑这一点。例如,要将均值为64,方差为400的高斯噪声添加到一幅uint8类图像上,需要将均值标度为64/255并将方差标度为400/(255^2)后,作为imnoise的输入。
g=imnoise(f,‘gaussian’,m,var) :将均值m,方差为var的高斯噪声添加到原图像上。默认值是均值m为0,方差var为0.01的噪声。
保持均值不变(0),方差增加,噪声干扰更大,分辨率降低,图像更加模糊。保持方差不变(0.01),均值增加,图像更白。
g=imnoise(f,‘localvar’,v): 将均值为0,局部方差为v的高斯噪声添加到原图像上。其中V是一个大小与f相同的数组,它在每个点包含了期望的方差值。
g=imnoise(f,‘localvar’,image_intensity,var):将均值为0的高斯噪声添加到图像f中,其中噪声的局部方差var是图像f的灰度值的函数。image_intensity和var是大小相同的向量。
g=imnoise(f,‘salt&pepper’,d) 用椒盐噪声污染图像f,其中d是噪声密度(即包含噪声值的图像区域的百分比),默认值为0.05。
g=imnoise(f,‘speckle’,var) 使用方程g=f+n.*f将乘性噪声添加到f上,其中n是均值为0,方差为var(默认为0.04)的均匀分布的随机噪声。
2.3 周期噪声
来源:图像在获取期间由电力或机电干扰产生的。
是本章中唯一一种空间相关噪声。
可通过频率域滤波器显著减少。
2.4 噪声参数估计
周期噪声的参数:通过检测图像的傅里叶谱来估计。
噪声PDF的参数:一般可从传感器的技术说明中得知;若只有图像可用时,通常由合理的恒定灰度值的一小部分来估计。
三、只存在噪声的复原——空间滤波(去噪复原)
即唯一的引起图像退化的原因是噪声。
故图像退化过程的形式如下:
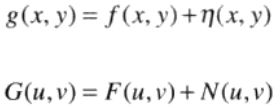
由于噪声项是未知的,故从g(x,y)或G(u,v)中减去它们不现实。
当仅存在加性噪声的情况下,可选择空间滤波方法,进行图像复原。
3.1 均值滤波器
3.1.1 算术均值滤波器
最简单的均值滤波器。
Sxy为中心点在(x,y),大小为m*n的邻域的一组坐标。算术均值滤波器在Sxy定义的区域中计算被污染图像g(x,y)的平均值。
假设m和n为奇整数。
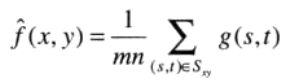
该操作可以使用大小为m x n的一个空间滤波器来实现,滤波器所有系数为其值的1/mn。
虽然是图像变模糊了,但是降低了噪声。
3.1.2 几何均值滤波器
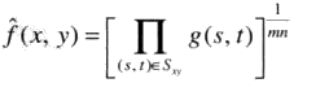
每个复原像素由Sxy区域内像素的乘积的1/mn次幂决定。
当实现图像平滑时,相比于算术均值滤波器,几何均值滤波器处理图像时,丢失的细节更少。
3.1.3 谐波均值滤波器

对于盐粒噪声效果较好,但不适用于高斯噪声。善于处理像高斯噪声那样的其他噪声。
3.1.4 逆谐波均值滤波器

其中,Q为滤波器阶数。该滤波器适合减少或消除椒盐噪声的影响。
当Q为正值时,该滤波器能消除胡椒噪声;当Q为负值使,能消除盐粒噪声。但该滤波器不能同时消除椒噪声和盐噪声。
当Q = 0时,逆谐波均值滤波器变成了算术均值滤波器,当Q = -1时,变成了谐波均值滤波器。
小结:
算术均值滤波器和几何均值滤波器(尤其是后者)更适合于处理高斯或均匀随机噪声;
逆谐波均值滤波器更适合处理椒盐噪声,但必须知道噪声是椒噪声还是盐噪声,以便为Q选择正确的符号,若符号选错,可能会引起灾难性的后果。
3.2 统计排序滤波器
3.2.1 中值滤波器
使用一个像素邻域中的灰度级排序的中值来替代该像素的值。
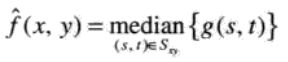
应用普遍,对某些类型的随机噪声能提供良好的去噪能力;与相同尺寸的线性平滑滤波器相比,引起的模糊更少。在存在单极或双极脉冲噪声(单独的椒噪声、单独的盐噪声、椒盐噪声)的情况下,只要噪声的空间密度不大(根据经验,Pa和Pb小于0.2),中值滤波器就很有效。
3.2.2 最大值和最小值滤波器
最大值滤波器:使用一个像素邻域中的灰度级排序的最后一个数值来替代该像素的值。
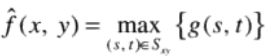
对发现图像中的最亮点非常有用。可以降低图像中的椒噪声。
最小值滤波器:使用一个像素邻域中的灰度级排序的起始值数值来替代该像素的值。
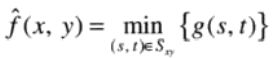
对发现图像中的最暗点非常有用。可以降低图像中的盐噪声。
img = imread('C:\Users\win\Desktop\dog.jpg');
img = rgb2gray(img);
I = imnoise(img,'salt & pepper',0.15); % 噪声密度为0.15
I1 = medfilt2(I); % 中值滤波
% ordfilt2(X,order,domain,S)二维顺序统计滤波函数
% X:为输入图像 order:滤波器输出的循序值 domain:滤波器窗口
% S:是与domain大小相同的矩阵,它是对应domain中非零值位置的输出偏置,这在图形形态学中是很有用的
I2 = ordfilt2(I,9,true(3)); % 最大值滤波器 true(3)表示创建3*3的方阵,方阵的所有元素都为逻辑真,即1
I3 = ordfilt2(I,1,true(3)); % 最小值滤波器
subplot(2,3,[1,2]);
imshow(img);
title('原图');
subplot(2,3,3);
imshow(I);
title('原图+椒盐噪声');
subplot(2,3,4);
imshow(I1,[]);
title('中值滤波');
subplot(2,3,5);
imshow(I1,[]);
title('最大值滤波');
subplot(2,3,6);
imshow(I1,[]);
title('最小值滤波');
3.2.3 中点滤波器
计算滤波器包围区域中最大值和最小值之间的中点。
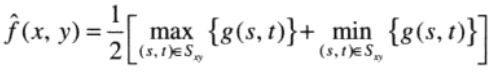
结合了统计排序和求平均。最适用于处理随机分布的噪声,如高斯噪声或均匀噪声。
3.2.4 修正的阿尔法均值滤波器
在邻域Sxy内去掉g(s,t)最低灰度值的d/2和最高灰度值的d/2。令gr(s,t)代表剩下的mn-d个像素。再对剩下的这些像素求平均值。
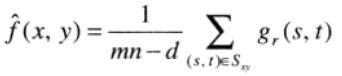
d的取值范围可为0 ~ mn-1。
当d = 0时,退化为算术均值滤波器;当d = mn-1时,退化为中值滤波器;当d取其他值时,该滤波器在包括多种噪声的情况下很有用,如混合有高斯噪声和椒盐噪声的情况。
3.3 自适应滤波器
考虑图像中的一点对其他点的特征变化,这些特征变化以m*n大小的Sxy定义的滤波器区域内图像的统计特性为基础。
自适应滤波器的性能更优,代价就是滤波器的复杂度提高了。
3.3.1 自适应局部降低噪声滤波器
随机变量最简单的统计度量是其均值和方差。均值给出了在其上计算均值的区域中的平均灰度的度量,方差则给出了该区域对比度的度量。
滤波器作用于Sxy区域。滤波器在Sxy区域中心任一点(x.y)上的响应基于以下4个量:
- g(x,y):带噪图像在点(x,y)上的值;
- ση2:污染f(x,y)以形成g(x,y)的噪声的方差(即全部噪声的方差);
- mL:Sxy中像素的局部均值;
- σL2:Sxy中像素的局部方差。
滤波器的性能:
- 若ση2 = 0 (即零噪声),f(x,y) = g(x,y)。
- 若σL2 > ση2,滤波器返回g(x,y)的近似值。高局部方差通常与边缘相关,并且应该保护这些边缘。
- 若σL2 = ση2,滤波器返回Sxy中像素的算术均值,即mL。(在局部区域与整个图像有相同特性的条件下,并且局部噪声将通过简单地求平均来降低)。
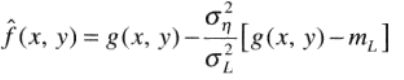
唯一需要知道或估计的量是ση2。
3.3.2 自适应中值滤波器
中值滤波器只是对脉冲噪声空间密度不大时,效果较好。
自适应中值滤波器可处理更大概率的脉冲噪声,在平滑非脉冲噪声时会试图保留细节。
自适应中值滤波也工作在Sxy区域内,但会根据某些条件改变(或增大)Sxy的尺寸。滤波器的输出是单个数值,用来代替中心点(x,y)的像素值。
符号描述:
- zmin = Sxy中的最小灰度值
- zmax = Sxy中的最大灰度值
- zmed = Sxy中的灰度值的中值
- zxy = 坐标(x,y)处的灰度值
- Smax = Sxy允许的最大尺寸
算法分为A、B两个进程工作:
进程A:
A1 = zmed - zmin
A2 = zmed - zmax
if A1 > 0 && A2 < 0 ,转到进程B
else 增大窗口尺寸
if 窗口尺寸 <= Smax ,重复进程A
else 输出zmed
进程B:
B1 = zxy - zmin
B2 = zxy - zmax
if B1 > 0 && B2 <0,输出zxy
else 输出zmed
可以使用**adpmedian()**函数来实现。语法为:
g = adpmedian(f,Smax)
算法的目的:
去除脉冲(椒盐)噪声;平滑其他非脉冲噪声;减少诸如物体边界细化或粗化等失真。
四、用频率域滤波消除周期噪声(去噪复原)
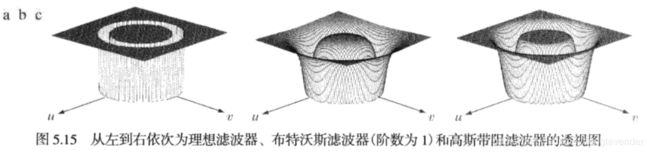
4.1 带阻滤波器
4.2 带通滤波器
与带阻滤波器的操作相反。
![]()
一般不会在图像上直接执行带通滤波,这样处理会使很多图像的细节消除。但可以提取噪声污染图像中的噪声模式。

4.3 陷波滤波器
陷波滤波器阻止(或通过)事先定义的中心频率的邻域内的频率。
具体参见数字图像处理——第四章(频率域滤波)
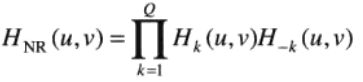
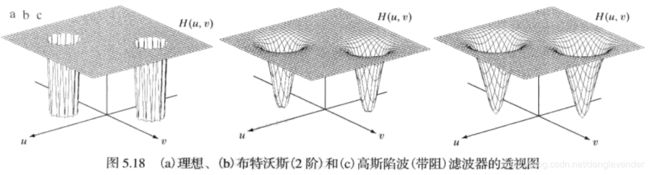
因为傅里叶变换具有对称性,要获得有效的结果,陷波滤波器必须以关于原点对称的形式出现,除非滤波器位于原点处。
陷波滤波器的对数是任意的,陷波区域的形状也可以是任意的。
![]()
HNP(u,v)为陷波带通滤波器的传递函数,HNR(u,v)为陷波带阻滤波器的传递函数。
4.4 最佳陷波滤波
提出背,当存在几种干扰成分时(即多周期性干扰)。在一定意义上,最佳陷波滤波最小化了复原的估计值的局部方差。
主要就是从污染图像中提取噪声模型,然后从污染图像中将噪声模型减去,以复原图像。
过程由两步组成:
1、提取干扰模式的主频率成分:
在每种周期噪声的尖峰处放一个陷波带通滤波器HNP(u,v),若滤波器构建为只可通过与干扰模式相关的成分,则干扰噪声模式的傅里叶变换如下:
![]()
G(u,v)为被污染图像的傅里叶变换。HNP(u,v)通常需要观察显示的G(u,v)的频谱交互式地创建陷波带通滤波器,来判断哪些是尖峰噪声干扰。
空间域的噪声表示如下:

2、从被污染图像中减去该模式的一个可变加权成分。
因为第一步提取的只是干扰模式的主要成分(即真实干扰模式的近似值),而不是全部的噪声,故从污染图像中减去的是η(x,y)的一个加权部分,得到f(x,y)的一个估计值。
![]()
w(x,y)称为加权函数或调制函数,该函数是待定的。
过程的目的就是选取加权函数,以便以某种有意义的方法来优化结果。
一种选取w(x,y)的方法:
使估计值在每一点(x,y)的指定邻域上的方差最小。
五、考虑图像退化函数
5.1 线性、位置不变的退化
前面介绍的退化图像的模型如下:
![]()
假设η(x,y)=0。则g(x,y) = H[f(x,y)]。
若
![]()
则H是一个线性系统。其中a和b是标量,f1(x,y)和f2(x,y)是两幅输入图像。
可加性
若a = b = 1,则
![]()
即,若H为线性算子,则两个输入之和的响应等于两个响应之和。
均匀性
若f2(x,y) = 0,则
![]()
表明任何与常数相乘的输入的响应,等于该输入响应乘以相同的常数。
总之,一个线性算子具有可加性和均匀性。
若一个算子满足
![]()
则满足g(x,y) = H[f(x,y)]的算子称为位置(或空间)不变系统。即,图像中任意一点处的响应只取决于该点处的输入值,而与该点的位置无关。
具有加性噪声的线性空间不变退化系统,可在空间域建模为退化(点扩散)函数与一幅图像的卷积,再加上噪声。频率域为图像与退化函数的变换的乘积,再加上噪声的变换。
用于复原处理的滤波器通常称为去卷积滤波器。
5.2 退化函数的估计
在图像复原时,往往真正的退化函数很少能完全知晓。
估计退化函数的方法:观察法、试验法、数学建模法。
5.2.1 图像观察估计
当没有退化函数的任何知识时,基于线性、位置不变的假设。通过选择退化图像的子图像(噪声要小到可以忽略,图像对比度要强),gs(x,y)表示子图像。

得到子图像的退化函数,从而基于位置不变的假设来还原完整图像的退化函数H(u,v)。
这种方法仅在特殊环境下使用的很麻烦的处理,如复原一幅有历史价值的老照片。
5.2.2 试验估计
使用或设计一个与图像退化过程相似的系统,在该系统下对一个冲激(小亮点)成像,可得到退化系统的冲激响应 H(u,v) 。
小亮点要足够亮,以便将噪声的影响降低到可忽略的程度。冲激的傅里叶变换是一个常量。
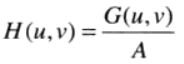
A是描述冲激强度的常量。

5.2.3 建模估计
由于退化建模能解决图像退化问题,故一直被使用。
大气湍流模型
![]()
其中,k为与湍流性质有关的常数,k越大,图像越模糊,除指数5/6外,与高斯低通滤波器有着相同的形式。
注意:在中心化图像的同时也要中心化H(u,v)函数,才能达到一 一对应的目的。
使用大气湍流模型来模糊图像。
atmospheric_turbulence .m
function [image_out] = atmospheric_turbulence (image_in,k)
% 输入image_in为初始灰度图像,大气湍流模型的系数k
% 输出为受大气湍流影响的图像
[m,n] = size(image_in);
%傅里叶变换
F = fft2(image_in);
F1 = fftshift(F); % 将零频率移到中心
% 中心点的坐标
p = m / 2 + 1.0;
q = n / 2 + 1.0;
%生成大气湍流模型函数
H = zeros(m,n);
for u = 1:m
for v = 1:n
temp = ((u-p)^2+(v-q)^2).^(5/6); % H也要和图像一样进行中心处理
H(u,v) = exp(-k*(temp));
end
end
% 得到退化图像
G = H.* F1;
% 反傅里叶变换
image_out = ifft2(ifftshift(G));
end
测试:
test.m
img = imread('C:\Users\win\Desktop\dog.jpg');
img = rgb2gray(img);
g1 = atmospheric_turbulence(img,0.0025);
g2 = atmospheric_turbulence(img,0.001);
g3 = atmospheric_turbulence(img,0.00025);
figure();
subplot(2,2,1);
imshow(img);
title('原图');
subplot(2,2,2);
imshow(g1,[]);
title('k = 0.0025(剧烈湍流)');
subplot(2,2,3);
imshow(g2,[]);
title('k = 0.001(中等湍流)');
subplot(2,2,4);
imshow(g3,[]);
title('k = 0.00025(轻微湍流)');
实验结果:

运动模糊模型
退化函数如下:

其中T表示曝光时间,a和b分别表示水平和垂直方向上的移动量。注意![]() ,故当π(ua+vb) = 0时,H(u,v) = T。同理,H(u.v)也要进行中心化。
,故当π(ua+vb) = 0时,H(u,v) = T。同理,H(u.v)也要进行中心化。
实现:
img = imread('C:\Users\win\Desktop\dog.jpg');
img = rgb2gray(img);
[m,n] = size(img);
%傅里叶变换
F = fft2(img);
F1 = fftshift(F); % 将零频率移到中心
% 中心点的坐标
p = m / 2 + 1.0;
q = n / 2 + 1.0;
%生成运动模糊模型函数
a = 0.1;
b = 0.1;
T = 1;
H = zeros(m,n);
for u = 1:m
for v = 1:n
temp = pi * ((u-p)*a + (v-q)*b); % H也要和图像一样进行中心化
if(temp == 0)
H(u,v) = T;
else
H(u,v) = T*(sin(temp)/temp)*exp(-1i*pi*temp); % 将复数i和j替换为1i以提高速度和增强稳定性
end
end
end
% 得到退化图像
G = H.* F1;
% 反傅里叶变换
g = ifft2(ifftshift(G));
figure();
subplot(1,2,1);
imshow(img);
title('原图');
subplot(1,2,2);
imshow(g,[]);
title('a = b = 0.1,T = 1的运动模糊图像');
5.3 逆滤波
知道退化函数后,最简单的复原方法就是直接做逆滤波。

上式表明,即使知道退化函数,也不能准确地复原未退化的图像,因为N(u,v)未知。而且,若H(u,v)是零或非常小的值,则N(u,v)/H(u,v)很容易支配估计值。
H(0,0)在频率域中通常是H(u,v)的最高值,即上一章说的直流分量,与频率的高低不是一个概念,H(0,0)处在频谱的最低频,但是是H(u,v)的频谱最高值。,即图像的频谱随着频率的升高而下降。
要解决退化函数为零或非常小的值,就要限制滤波的频率,使其接近原点。具体有如下两种方法:
1)可以对G(u,v)/H(u,v)应用一个低通滤波器,虑去其中病态的高频成分(即虑去H(u,v)中接近0的部分)
2)或者规定一个值,当|H(u,v)| ≤ δ 时,1/H(u,v) = 0。
当退化图像的噪声较小,即轻度降质时,采用逆滤波恢复的方法可以获得较好的结果。
当噪声作用范围很大时,逆滤波不能从噪声中提取图像。
一般直接逆滤波的性能是较差的。故接下来介绍的三种滤波都是对直接滤波的改进。
5.4 最小均方误差(维纳)滤波
维纳滤波建立在最下统计化准则的基础上。
寻找一个未污染图像的估计值,使得他们之间的均方误差最小。
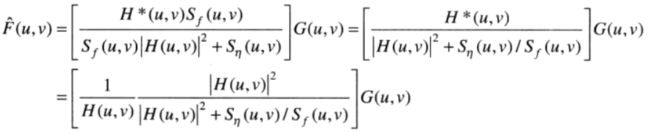

当处理白噪声时,噪声功率谱是一个常数,但未退画图像的功率谱很少是已知的,故经常用下面的式子来近似表示。

其中|H(u,v)|2 = H*(u,v)H(u,v),H(u,v)为退化函数,H*(u,v)为H(u,v)的共轭复数。
其中K是一个特定的常数,与噪声和未退化图像之间的信噪比有关。不同情况下取值不同。在平均意义下是最优的。
5.5 约束最小二乘方滤波
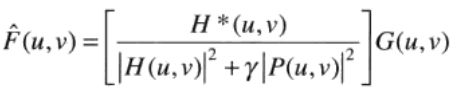
其中γ是一个参数,可以对γ进行交互式的调整,也可以对其进行迭代计算。P(u,y)是矩阵p(x,y) = [0, -1, 0; -1, 4,-1; 0, -1, 0]的傅里叶变换。该算法相比于维纳滤波,对其应用的每幅图像都能产生最优的结果。
5.6 几何均值滤波
几何均值滤器是对维纳滤波器的一点点推广。
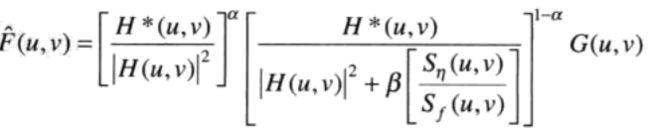
其中α和β为正的实常数。
实现
使用运动模型作为退化函数,并加入高斯噪声,对上述几种滤波器进行对比。
img = imread('C:\Users\win\Desktop\dog.jpg');
I = rgb2gray(img);
[m,n] = size(I);
% 频率中心
p = m/2 + 1.0;
q = n/2 + 1.0;
% 维纳滤波参数K
K = 0.05;
% 约束最小二乘方参数
y = 0.5;
% 高斯噪声的均值M和方差V
M = 0; V = 500;
% 对原图进行傅里叶变换及中心化
F = fftshift(fft2(I));
% 生成高斯噪声的傅里叶变换
noise = 0 + 500.^0.5 * randn(m,n);
Fn = fftshift(fft2(noise));
%生成运动模糊模型函数
a = 0.1;
b = 0.1;
T = 1;
H = zeros(m,n);
for u = 1:m
for v = 1:n
temp = pi * ((u-p)*a + (v-q)*b); % H也要和图像一样进行中心化
if(temp == 0)
H(u,v) = T;
else
H(u,v) = T*(sin(temp)/temp)*exp(-1i*pi*temp); % 将复数i和j替换为1i以提高速度和增强稳定性
end
end
end
% 维纳滤波器
Hwiener = (abs(H).^2) ./ (abs(H).^2 + K) ./ H;
% 约束最小二乘方滤波器
p = [0,-1,0;-1,4,-1;0,-1,0];
FP = fftshift(fft2(p,m,n)); % 矩阵的傅里叶变换
Hleast = conj(H) ./ (abs(H).^2 + y*abs(FP).^2); % conj()求共轭复数
% 生成退化图像,即运动模糊模型+高斯噪声
G1 = F.* H + Fn;
f1 = ifft2(ifftshift(G1));
% f1 = real(fg1); % 取傅里叶反变换的实部
% 将退化图像归一化到[0,255]
image = zeros(m,n);
mmax = max(f1(:));
mmin = min(f1(:));
range = mmax - mmin;
for i = 1:m
for j = 1:n
image(i,j) = uint8(255 * (f1(i,j) - mmin) / range);
end
end
% 为了接近真实情况,对归一化后的退化图像进行复原操作(去卷积)
G2 = fftshift(fft2(image));
% 直接逆滤波
F2 = G2 ./ H;
f2 = ifft2(ifftshift(F2));
% 维纳滤波
F3 = G2 .* Hwiener;
f3 = ifft2(ifftshift(F3));
% 约束最小二乘方滤波
F4 = G2 .* Hleast;
f4 = ifft2(ifftshift(F4));
figure();
subplot(2,3,1);
imshow(I);
title('原图');
subplot(2,3,2);
imshow(f1,[]);
title('退化图像');
subplot(2,3,3);
imshow(f2,[]);
title('直接逆滤波图像');
subplot(2,3,4);
imshow(f3,[])
title('维纳滤波图像');
subplot(2,3,5);
imshow(f4,[]);
title('约束最小二乘方滤波图像');