禁忌搜索算法（TABU）解决路线规划问题（CVRP）

禁忌搜索算法解决路线规划问题

问题定义

车辆路线规划问题是一个经典的组合优化问题，也是旅行商问题的泛化。该问题的定义为：

• 有给定数量的客户有运输需求；
• 为从某个固定地点出发和返回的车辆寻找一个最优路线试的可以服务所有的客户
  车辆路线规划问题是NP-hard问题，一般建议求最优解的近似解。

车辆路线规划问题有很多变种，主要包含 Classical VRP（VRP）、 Capacitated Vehicle Routing Problem (CVRP)、 Vehicle Routing Problem with Time Windows (VRPTW)、 Vehicle Routing Problem with Pick-Up and Delivery (VRPPD)等。现实生活中VRP模型用处较少，其它都很常见；CVRP对应配送中心对配送站点的送货，VRPTW则面向客户的送货，如外卖；VRPPD对应取货和送货，如京东快递即可以送快递又可以取快递。

本本主要套餐CVRP，其定义如下：

令G =（V，A)表示一个有向图，其中V是顶点集，而A是弧集。一个顶点表示 m个容量为Q的相同车辆组成的车队所在的仓库，其它顶点表示要服务的客户。每个客户顶点vi与需求qi关联。每个弧（vi，vj）通过A与耗费成本cij相关联。 CVRP目标是找到一系列路线，以便：

• 每条路线以仓库为起始点;
• 每个用户仅被服务一次;
• 每条路线的需求量不超过Q;
• 所有路线总消耗成本最小;

CVRP问题解决算法

本文使用贪心算法（Greedy Algorithm）初始解决方案，使用禁忌搜索算法（Tabu Search Algorithm）进行优化并求得最优解；测试用例来源为http://vrp.atd-lab.inf.puc-rio.br/index.php/en/

禁忌搜索算法

禁忌搜索算法是一种应用局部搜索的启发式搜索算法；

局部搜索的两种策略

1)选定一个可行的初始解，定义邻域。从邻域中找到最好的解与初始解比较，然后取最小的解为新的初始解。如此迭代直到解满足一定条件后停止。
2）随机法。从初始可行解邻域中随机选择一点，与初始解比较，循环直到解的质量达到一定程度。

局部搜索的缺点

1)无法保证得到全局最优解。
2）解的质量依赖于起始点和领域的选取。
3）为了得到高质量的解，需要比较不同的邻域结构和初始解，只有在选择足够多时，才能保证得到最优解。

禁忌搜索算法的提出

禁忌搜索（Tabu Search)是局部领域算法的推广，Fred Glover Fred Glover在1986年提出这个概念，进而进一步形成一套完整的算法。算法的特点就是禁忌，禁止重复前面的工作，跳出局部最优点。

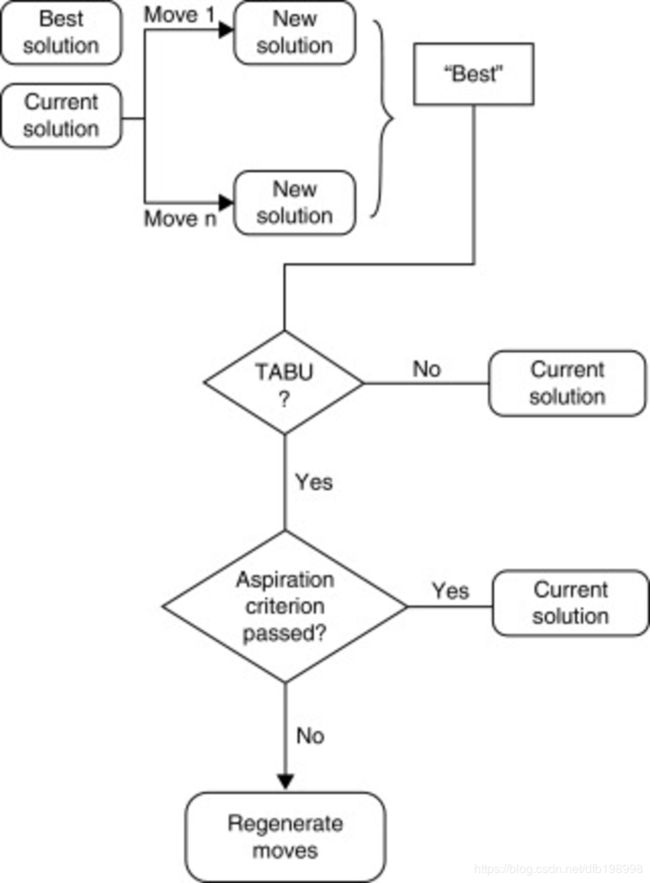
禁忌搜索算法流程图

禁忌搜索算法伪码

     1 sBest ← s0
     2 bestCandidate ← s0
     3 tabuList ← []
     4 tabuList.push(s0)
     5 while (not stoppingCondition())
     6 	sNeighborhood ← getNeighbors(bestCandidate)
     7 	bestCandidate ← sNeighborHood.firstElement
     8 	for (sCandidate in sNeighborHood)
     9 		if ( (not tabuList.contains(sCandidate)) and (fitness(sCandidate) > fitness(bestCandidate)) )
    10 			bestCandidate ← sCandidate
    11 		end
    12 	end
    13 	if (fitness(bestCandidate) > fitness(sBest))
    14 		sBest ← bestCandidate
    15 	end
    16 	tabuList.push(bestCandidate)
    17 	if (tabuList.size > maxTabuSize)
    18 		tabuList.removeFirst()
    19 	end
    20 end
    21 return sBest

算法结果

统计结果

实例	客户数	采用禁忌搜索算法前.	采用禁忌搜索算法后	用例目前最优解
A-n32-k5	32	903.7	787.08	784
A-n60-k9	60	1464.09	1362.38	1408
A-n80-k10	80	1845.08	1828.28	1764
B-n78-k10	78	1421.76	1315.22	1266
P-n101-k4	101	771.68	715.89	681

详细结果

使用禁忌搜索算法解决CVRP部分结果如下，测试用例来源为Capacitated Vehicle Routing Problem Library

• A-n32-k5
  Vehicle 1: 1(0)->13(21)->2(19)->17(18)->31(14)->1(0) totalDemand = 72.0
  Vehicle 2: 1(0)->28(20)->25(24)->1(0) totalDemand = 44.0
  Vehicle 3: 1(0)->22(12)->32(9)->20(24)->18(19)->14(16)->8(16)->27(2)->1(0) totalDemand = 98.0
  Vehicle 4: 1(0)->7(12)->4(6)->3(21)->24(8)->5(19)->12(14)->29(15)->15(3)->1(0) totalDemand = 98.0
  Vehicle 5: 1(0)->21(8)->6(7)->26(24)->11(8)->30(2)->16(22)->23(4)->10(16)->9(6)->19(1)->1(0) totalDemand = 98.0
  最优解: 787.08

• A-n60-k9
  Vehicle 1: 1(0)->42(21)->34(6)->39(14)->60(23)->53(18)->1(0) totalDemand = 82.0
  Vehicle 2: 1(0)->17(11)->21(1)->4(7)->12(19)->41(11)->47(1)->26(18)->1(0) totalDemand = 68.0
  Vehicle 3: 1(0)->35(9)->25(24)->59(9)->24(23)->48(17)->15(13)->1(0) totalDemand = 95.0
  Vehicle 4: 1(0)->36(5)->56(9)->51(4)->40(19)->27(19)->18(24)->28(2)->30(17)->1(0) totalDemand = 99.0
  Vehicle 5: 1(0)->5(11)->22(5)->54(21)->31(9)->50(2)->45(18)->29(17)->7(17)->1(0) totalDemand = 100.0
  Vehicle 6: 1(0)->19(2)->8(21)->14(20)->38(2)->58(22)->9(23)->20(3)->1(0) totalDemand = 93.0
  Vehicle 7: 1(0)->3(2)->2(16)->49(42)->23(20)->37(9)->32(11)->1(0) totalDemand = 100.0
  Vehicle 8: 1(0)->16(5)->44(21)->57(18)->13(18)->52(24)->10(10)->33(2)->1(0) totalDemand = 98.0
  Vehicle 9: 1(0)->11(6)->55(11)->6(9)->43(20)->46(48)->1(0) totalDemand = 94.0
  最优解: 1362.38

• A-n80-k10
  Vehicle 1: 1(0)->50(13)->37(12)->39(23)->67(11)->68(5)->74(12)->1(0) totalDemand = 76.0
  Vehicle 2: 1(0)->2(24)->8(26)->22(13)->41(13)->1(0) totalDemand = 76.0
  Vehicle 3: 1(0)->59(7)->77(14)->33(9)->46(23)->5(5)->23(26)->51(10)->71(5)->1(0) totalDemand = 99.0
  Vehicle 4: 1(0)->14(12)->75(19)->30(10)->18(20)->32(2)->60(22)->28(4)->6(11)->1(0) totalDemand = 100.0
  Vehicle 5: 1(0)->11(9)->72(12)->64(22)->63(18)->24(17)->45(6)->13(16)->1(0) totalDemand = 100.0
  Vehicle 6: 1(0)->54(13)->4(23)->61(13)->40(21)->78(2)->43(23)->1(0) totalDemand = 95.0
  Vehicle 7: 1(0)->73(2)->55(2)->10(23)->56(14)->57(7)->70(9)->66(2)->36(2)->27(4)->48(2)->20(12)->76(6)->21(15)->1(0) totalDemand = 100.0
  Vehicle 8: 1(0)->52(3)->65(6)->34(1)->16(2)->42(13)->47(11)->26(12)->58(21)->62(22)->31(9)->1(0) totalDemand = 100.0
  Vehicle 9: 1(0)->35(2)->3(22)->38(14)->9(9)->44(3)->17(6)->69(9)->79(2)->7(23)->25(7)->1(0) totalDemand = 97.0
  Vehicle 10: 1(0)->12(14)->53(6)->29(20)->80(24)->49(7)->19(26)->15(2)->1(0) totalDemand = 99.0

最优解: 1828.28

• B-n78-k10
  Vehicle 1: 1(0)->18(6)->73(12)->59(3)->22(5)->25(3)->53(23)->2(14)->1(0) totalDemand = 66.0
  Vehicle 2: 1(0)->39(14)->70(12)->44(11)->68(14)->57(9)->28(23)->3(17)->1(0) totalDemand = 100.0
  Vehicle 3: 1(0)->66(13)->76(4)->38(14)->71(23)->31(4)->6(19)->64(20)->1(0) totalDemand = 97.0
  Vehicle 4: 1(0)->78(19)->24(4)->45(21)->27(4)->12(2)->65(5)->41(5)->54(25)->1(0) totalDemand = 85.0
  Vehicle 5: 1(0)->50(12)->30(21)->74(15)->77(23)->8(5)->58(21)->48(2)->1(0) totalDemand = 99.0
  Vehicle 6: 1(0)->9(12)->13(26)->16(18)->52(14)->33(6)->21(14)->55(8)->1(0) totalDemand = 98.0
  Vehicle 7: 1(0)->43(14)->26(15)->11(2)->69(16)->19(18)->17(6)->67(6)->61(6)->7(17)->1(0) totalDemand = 100.0
  Vehicle 8: 1(0)->72(5)->23(9)->35(4)->47(18)->46(20)->32(1)->4(17)->63(22)->1(0) totalDemand = 96.0
  Vehicle 9: 1(0)->51(22)->62(2)->40(26)->49(19)->75(21)->29(7)->1(0) totalDemand = 97.0
  Vehicle 10: 1(0)->42(2)->15(7)->37(5)->5(16)->60(22)->36(20)->56(3)->34(16)->14(2)->20(2)->10(4)->1(0) totalDemand = 99.0

最优解: 1315.22

• P-n101-k4
  Vehicle 1: 1(0)->54(14)->59(18)->41(9)->22(11)->74(9)->73(25)->75(8)->76(18)->57(6)->5(19)->55(18)->81(6)->69(36)->78(14)->4(13)->80(23)->34(11)->82(26)->10(16)->52(10)->51(13)->77(13)->13(19)->27(17)->29(16)->1(0) totalDemand = 388.0
  Vehicle 2: 1(0)->53(9)->8(5)->83(16)->49(36)->20(17)->48(27)->47(1)->37(5)->50(30)->65(9)->12(12)->64(10)->91(3)->33(23)->11(16)->63(19)->89(9)->32(27)->28(16)->1(0) totalDemand = 290.0
  Vehicle 3: 1(0)->95(27)->7(3)->97(11)->100(9)->60(28)->94(22)->86(41)->101(17)->92(1)->45(18)->15(20)->39(16)->87(35)->17(19)->62(13)->6(26)->85(7)->18(2)->46(16)->9(9)->84(11)->61(3)->19(12)->90(15)->1(0) totalDemand = 381.0
  Vehicle 4: 1(0)->14(23)->96(20)->93(2)->99(10)->38(8)->98(12)->88(26)->43(5)->44(7)->16(8)->58(7)->3(7)->42(5)->23(18)->24(29)->68(25)->40(31)->26(6)->56(2)->25(3)->30(9)->79(3)->35(14)->36(8)->72(15)->66(20)->67(25)->21(9)->31(21)->71(5)->2(10)->70(6)->1(0) totalDemand = 399.0

最优解: 715.89

结论

1. 禁忌搜索是解决路线规划问题的优秀算法
2. 无法保证一定能获得最优解，这取决与具体问题参数选择，一般执行次数越多效果约好

代码清单

读取测试数据

public class VRPLibReader {

    private InstanceReader reader;

    private int dimension;
    private int vehicleCapacity;
    private double[][] coord;
    private double[][] distance;
    private int[] demand;
    private double[][] pickup;
    private LocalTime[][] timeWindows;
    private int[] standTime;
    private int[] depots;

    public VRPLibReader(InstanceReader reader) {
        this.reader = reader;

        readHeader();
        readCoordinates();
        readDemand();
        convertCoordToDistance();
    }

    private void readHeader() {
        String line = reader.readLine();

        while (!line.equalsIgnoreCase("NODE_COORD_SECTION")) {
            String[] split = line.split(":");

            String key = split[0].trim();

            if (key.equalsIgnoreCase("DIMENSION")) {
                dimension = Integer.valueOf(split[1].trim());
            }

            if (key.equalsIgnoreCase("CAPACITY")) {
                vehicleCapacity = Integer.valueOf(split[1].trim());
            }

            line = reader.readLine();

            if (line == null) {
                break;
            }
        }
    }

    private void readCoordinates() {
        coord = new double[dimension][2];

        String line = reader.readLine();
        while (!line.equalsIgnoreCase("DEMAND_SECTION")) {
            parseRow(line, coord);

            line = reader.readLine();
        }
    }

    private void parseRow(String line, double[][] coord) {
        String[] split = line.split("\\s+");

        int i = Integer.valueOf(split[0].trim()) - 1;
        coord[i][0] = Double.valueOf(split[1].trim());
        coord[i][1] = Double.valueOf(split[2].trim());
    }

    private void readDemand() {
        demand = new int[dimension];

        String line = reader.readLine();
        while (!line.equalsIgnoreCase("DEPOT_SECTION")) {

            String[] split = line.split("\\s+");

            int i = Integer.valueOf(split[0].trim()) - 1;
            demand[i] = Integer.valueOf(split[1].trim());

            line = reader.readLine();
        }
    }

    private void readPickup() {
        pickup = new double[dimension][2];

        String line = reader.readLine();
        while (!line.equalsIgnoreCase("TIME_WINDOW_SECTION")) {
            parseRow(line, pickup);

            line = reader.readLine();
        }
    }

    private void readTimeWindows() {
        timeWindows = new LocalTime[dimension][2];

        String line = reader.readLine();
        while (!line.equalsIgnoreCase("STANDTIME_SECTION")) {
            String[] split = line.split("\\s+");

            int i = Integer.valueOf(split[0].trim()) - 1;

            String startTime = split[1].trim();
            String endTime = split[2].trim();
            if (startTime.equals("")) {
                startTime = "0" + split[2].trim();
                endTime = split[3].trim();

                if (endTime.equals("")) {
                    endTime = "0" + split[4].trim();
                }
            }

            timeWindows[i][0] = LocalTime.parse(startTime);
            timeWindows[i][1] = LocalTime.parse(endTime);

            line = reader.readLine();
        }
    }

    private void readStandtime() {
        standTime = new int[dimension];

        String line = reader.readLine();
        while (!line.equalsIgnoreCase("DEPOT_SECTION")) {
            String[] split = line.split("\\s+");

            int i = Integer.valueOf(split[0].trim()) - 1;
            standTime[i] = Integer.valueOf(split[1].trim());

            line = reader.readLine();
        }
    }

    private void readDepots() {
        depots = new int[2];

        String line = reader.readLine();
        int i = 0;
        while (!line.equalsIgnoreCase("EOF")) {
            depots[i] = Double.valueOf(line.trim()).intValue();
            i++;

            line = reader.readLine();
        }
    }

    private void convertCoordToDistance() {
        distance = new double[dimension][dimension];

        for (int i = 0; i < dimension; i++) {
            for (int j = i; j < dimension; j++) {
                if (i != j) {
                    double x1 = coord[i][0];
                    double y1 = coord[i][1];
                    double x2 = coord[j][0];
                    double y2 = coord[j][1];

                    distance[i][j] = euclideanDistance(x1, y1, x2, y2);
                    distance[j][i] = distance[i][j];
                }
            }
        }
    }

    private static double euclideanDistance(double x1, double y1, double x2, double y2) {
        double xDistance = Math.abs(x1 - x2);
        double yDistance = Math.abs(y1 - y2);

        return Math.sqrt(Math.pow(xDistance, 2) + Math.pow(yDistance, 2));
    }

    public int getDimension() {
        return dimension;
    }

    public double[][] getDistance() {
        return distance;
    }

    public int getVehicleCapacity() {
        return vehicleCapacity;
    }

    public int[] getDemand() {
        return demand;
    }

    public int[] getDepots() {
        return depots;
    }

    private static final double EARTH_RADIUS = 6371.393; // 平均半径,单位：km

    /**
     * 通过AB点经纬度获取距离
     * @return 距离(单位：米)
     */
    public static double getDistance(double x1, double y1, double x2, double y2) {
        // 经纬度（角度）转弧度。弧度用作参数，以调用Math.cos和Math.sin
        double radiansAX = Math.toRadians(y1); // A经弧度
        double radiansAY = Math.toRadians(x1); // A纬弧度
        double radiansBX = Math.toRadians(y2); // B经弧度
        double radiansBY = Math.toRadians(x2); // B纬弧度

        // 公式中“cosβ1cosβ2cos（α1-α2）+sinβ1sinβ2”的部分，得到∠AOB的cos值
        double cos = Math.cos(radiansAY) * Math.cos(radiansBY) * Math.cos(radiansAX - radiansBX)
                + Math.sin(radiansAY) * Math.sin(radiansBY);
        double acos = Math.acos(cos); // 反余弦值
        return EARTH_RADIUS * acos; // 最终结果

    }
}

初始解

public class GreedySolver {
    private final int noOfVehicles;
    private final Node[] nodes;
    private final double[][] distances;
    private final int noOfCustomers;
    private final Vehicle[] vehicles;

    private double cost;

    public GreedySolver(VRPRunner jct) throws IOException {
        VRPLibReader reader = new VRPLibReader(new InstanceReader(new File(jct.instance)));
        this.noOfCustomers = reader.getDimension();
        this.noOfVehicles = reader.getDimension();
        this.distances = reader.getDistance();
        this.cost = 0;

        nodes = new Node[noOfCustomers];

        for (int i = 0; i < noOfCustomers; i++) {
            nodes[i] = new Node(i, reader.getDemand()[i]);
        }

        this.vehicles = new Vehicle[this.noOfVehicles];

        for (int i = 0; i < this.noOfVehicles; i++) {
            vehicles[i] = new Vehicle(reader.getVehicleCapacity());
        }
    }

    private boolean unassignedCustomerExists(Node[] Nodes) {
        for (int i = 1; i < Nodes.length; i++) {
            if (!Nodes[i].IsRouted)
                return true;
        }
        return false;
    }

    public GreedySolver solve() {
        double CandCost, EndCost;
        int VehIndex = 0;

        while (unassignedCustomerExists(nodes)) {
            int CustIndex = 0;
            Node Candidate = null;
            double minCost = (float) Double.MAX_VALUE;

            if (vehicles[VehIndex].routes.isEmpty()) {
                vehicles[VehIndex].AddNode(nodes[0]);
                if(!nodes[CustIndex].IsRouted) {
                    nodes[CustIndex].IsRouted = true;  //不会被当成真实节点
                }

            }

            for (int i = 0; i < noOfCustomers; i++) {
                if (!nodes[i].IsRouted) {
                    if (vehicles[VehIndex].initCheckIfFits(nodes[i].demand)) {
                        CandCost = distances[vehicles[VehIndex].currentLocation][i];
                        if (minCost > CandCost) {
                            minCost = CandCost;
                            CustIndex = i;
                            Candidate = nodes[i];
                        }
                    }
                }
            }

            if (Candidate == null) {
                //Not a single Customer Fits
                if (VehIndex + 1 < vehicles.length) //We have more vehicles to assign
                {
                    if (vehicles[VehIndex].currentLocation != 0) {//End this route
                        EndCost = distances[vehicles[VehIndex].currentLocation][0];
                        vehicles[VehIndex].AddNode(nodes[0]);
                        this.cost += EndCost;
                    }
                    VehIndex = VehIndex + 1; //Go to next Vehicle
                } else //We DO NOT have any more vehicle to assign. The problem is unsolved under these parameters
                {
                    System.out.println("\nThe rest customers do not fit in any Vehicle\n" +
                            "The problem cannot be resolved under these constrains");
                    System.exit(0);
                }
            } else {
                vehicles[VehIndex].AddNode(Candidate);//If a fitting Customer is Found
                nodes[CustIndex].IsRouted = true;
                this.cost += minCost;
            }
        }

        EndCost = distances[vehicles[VehIndex].currentLocation][0];
        vehicles[VehIndex].AddNode(nodes[0]);
        this.cost += EndCost;

        return this;
    }

    public void print() {
        System.out.println("=========================================================");

        for (int j = 0; j < noOfVehicles; j++) {
            if (!vehicles[j].routes.isEmpty()) {
                System.out.print("Vehicle " + j + ":");
                int RoutSize = vehicles[j].routes.size();
                for (int k = 0; k < RoutSize; k++) {
                    if (k == RoutSize - 1) {
                        System.out.print(vehicles[j].routes.get(k).NodeId);
                    } else {
                        System.out.print(vehicles[j].routes.get(k).NodeId + "->");
                    }
                }
                System.out.println();
            }
        }
        System.out.println("\nBest Value: " + this.cost + "\n");
    }

    public Vehicle[] getVehicles() {
        return vehicles;
    }

    public double getCost() {
        return cost;
    }
}

禁忌搜索解法

public class TabuSearchSolver {
    private final double[][] distances;
    private final int noOfVehicles;
    private final int TABU_Horizon;
    private final int iterations;
    private final Vehicle[] BestSolutionVehicles;

    private Vehicle[] vehicles;
    private double cost;

    private double BestSolutionCost;

    public TabuSearchSolver(VRPRunner jct) throws IOException {
        VRPLibReader reader = new VRPLibReader(new InstanceReader(new File(jct.instance)));
        this.noOfVehicles = reader.getDimension();
        this.TABU_Horizon = jct.TabuHorizon;
        this.distances = reader.getDistance();
        this.iterations = jct.iterations;

        GreedySolver greedySolver = new GreedySolver(jct);
        greedySolver.solve();
        this.vehicles = greedySolver.getVehicles();
        this.cost = greedySolver.getCost();

        this.BestSolutionVehicles = new Vehicle[this.noOfVehicles];

        for (int i = 0; i < this.noOfVehicles; i++) {
            this.BestSolutionVehicles[i] = new Vehicle(reader.getVehicleCapacity());
        }
    }

    public TabuSearchSolver solve() {
        //We use 1-0 exchange move
        ArrayList<Node> routesFrom;
        ArrayList<Node> routesTo;

        int MovingNodeDemand = 0;

        int VehIndexFrom, VehIndexTo;
        double BestNCost, NeighborCost;

        int SwapIndexA = -1, SwapIndexB = -1, SwapRouteFrom = -1, SwapRouteTo = -1;
        int iteration_number = 0;

        int DimensionCustomer = this.distances[1].length;
        int TABU_Matrix[][] = new int[DimensionCustomer + 1][DimensionCustomer + 1];

        this.BestSolutionCost = this.cost;
        Vehicle toVehicle = null;
        Vehicle fromVehicle = null;


        while (iteration_number < iterations) {
            BestNCost = Double.MAX_VALUE;

            for (VehIndexFrom = 0; VehIndexFrom < this.vehicles.length; VehIndexFrom++) {
                routesFrom = this.vehicles[VehIndexFrom].routes;
                int RoutFromLength = routesFrom.size();

                for (int i = 1; i < (RoutFromLength - 1); i++) { //Not possible to move depot!


                    for (VehIndexTo = 0; VehIndexTo < this.vehicles.length; VehIndexTo++) {
                        routesTo = this.vehicles[VehIndexTo].routes;
                        int RouteToLength = routesTo.size();
                        for (int j = 0; (j < RouteToLength - 1); j++) {//Not possible to move after last Depot!

                            MovingNodeDemand = routesFrom.get(i).demand;

                            if ((VehIndexFrom == VehIndexTo) || this.vehicles[VehIndexTo].CheckIfFits(MovingNodeDemand)) {
                                //If we assign to a different route check capacity constrains
                                //if in the new route is the same no need to check for capacity

                                if (!((VehIndexFrom == VehIndexTo) && ((j == i) || (j == i - 1))))  // Not a move that Changes solution cost
                                {
                                    // minnus length after remove from fromRouting, and insert into to toRouting
                                    double MinusCost1 ;
                                    }
                                }
                            }
                        }
                    }
                }
            }

            for (int o = 0; o < TABU_Matrix[0].length; o++) {
                for (int p = 0; p < TABU_Matrix[0].length; p++) {
                    if (TABU_Matrix[o][p] > 0) {
                        TABU_Matrix[o][p]--;
                    }
                }
            }

            routesFrom = this.vehicles[SwapRouteFrom].routes;
            routesTo = this.vehicles[SwapRouteTo].routes;
            this.vehicles[SwapRouteFrom].routes = null;
            this.vehicles[SwapRouteTo].routes = null;

            Node SwapNode = routesFrom.get(SwapIndexA);

            int NodeIDBefore = routesFrom.get(SwapIndexA - 1).NodeId;
            int NodeIDAfter = routesFrom.get(SwapIndexA + 1).NodeId;
            int NodeID_F = routesTo.get(SwapIndexB).NodeId;
            int NodeID_G = routesTo.get(SwapIndexB + 1).NodeId;

            Random TabuRan = new Random();
            int randomDelay1 = TabuRan.nextInt(5);
            int randomDelay2 = TabuRan.nextInt(5);
            int randomDelay3 = TabuRan.nextInt(5);

            routesFrom.remove(SwapIndexA);

            if (SwapRouteFrom == SwapRouteTo) {
                if (SwapIndexA < SwapIndexB) {
                    routesTo.add(SwapIndexB, SwapNode);
                } else {
                    routesTo.add(SwapIndexB + 1, SwapNode);
                }
            } else {
                routesTo.add(SwapIndexB + 1, SwapNode);
            }

            // update vehicle load
            this.vehicles[SwapRouteFrom].routes = routesFrom;
            this.vehicles[SwapRouteFrom].load -= SwapNode.demand;

            this.vehicles[SwapRouteTo].routes = routesTo;
            this.vehicles[SwapRouteTo].load += SwapNode.demand;

            this.cost += BestNCost;

            if (this.cost < this.BestSolutionCost) {
                iteration_number = 0;
                this.SaveBestSolution();
            } else {
                iteration_number++;
            }
        }

        this.vehicles = this.BestSolutionVehicles;
        this.cost = this.BestSolutionCost;

        return this;
    }

    public boolean exceedMaxLoad(List<Node> nodes, int capacity) {
        double vechileTotalDemand = 0;
        for(Node node : nodes) {
            vechileTotalDemand += node.demand;
        }
        return vechileTotalDemand > capacity;
    }

    private void SaveBestSolution() {
        this.BestSolutionCost = this.cost;
        for (int j = 0; j < this.noOfVehicles; j++) {
            this.BestSolutionVehicles[j].routes.clear();
            if (!this.vehicles[j].routes.isEmpty()) {
                int RoutSize = this.vehicles[j].routes.size();
                for (int k = 0; k < RoutSize; k++) {
                    Node n = this.vehicles[j].routes.get(k);
                    this.BestSolutionVehicles[j].routes.add(n);
                }
            }
        }
    }

    public void print() {
        System.out.println("==========================the result===============================");
        int vechileCount = 1;
        for (int j = 0; j < this.noOfVehicles; j++) {
            if (!this.vehicles[j].routes.isEmpty() && this.vehicles[j].routes.size() > 2) {
                System.out.print("Vehicle " + vechileCount + ": ");
                int RoutSize = this.vehicles[j].routes.size();
                for (int k = 0; k < RoutSize; k++) {
                    Node node = this.vehicles[j].routes.get(k);
                    if (k == RoutSize - 1) {
                        System.out.print((node.NodeId + 1) + "("+ node.demand +")");
                    } else {
                        System.out.print((node.NodeId) + 1 + "("+ node.demand +")" + "->");
                    }
                }
                System.out.println(" totalDemand = " + getDemand(this.vehicles[j].routes));
                ++vechileCount;
            }
        }
        System.out.println("\nBest Value: " + this.cost + "\n");
    }

    private double getDemand(List<Node> nodes) {
        double vechileTotalDemand = 0;
        for(Node node : nodes) {
            vechileTotalDemand += node.demand;
        }
        return vechileTotalDemand;
    }
}

程序入口

public class VRPRunner {
    @Parameter(names = {"--algorithm", "-alg"}, required = true)
    private String alg = "tabu";
    @Parameter(names = {"--instance", "-i"})
    public String instance = "datasets/big/Golden_20.vrp";
    @Parameter(names = "--iterations")
    public int iterations = 1000;
    @Parameter(names = "--tabu")
    public Integer TabuHorizon = 10;

    public static void main(String[] args) throws IOException {
        VRPRunner jct = new VRPRunner();
        JCommander jCommander = new JCommander(jct);
        jCommander.setProgramName(VRPRunner.class.getSimpleName());

        switch (jct.alg) {
            case "tabu": {
                new TabuSearchSolver(jct)
                        .solve()
                        .print();
                break;
            }
            default:
            case "greedy": {
                new GreedySolver(jct)
                        .solve()
                        .print();
                break;
            }
        }
    }
}