小陈的开学第八周程序
目录
- @[TOC](目录)
- 一、codeforces
- 1.Good ol' Numbers Coloring
- 2.Restricted RPS
- 二、Atcoder
- 1. ><
- 三、Wlacm
- 1.牛的旅行
- 2.香甜的黄油
- 四、Vjudge
- 1.find the mincost route
目录
- @[TOC](目录)
- 一、codeforces
- 1.Good ol' Numbers Coloring
- 2.Restricted RPS
- 二、Atcoder
- 1. ><
- 三、Wlacm
- 1.牛的旅行
- 2.香甜的黄油
- 四、Vjudge
- 1.find the mincost route
一、codeforces
1.Good ol’ Numbers Coloring
题意:
Consider the set of all nonnegative integers: 0,1,2,…. Given two integers a and b (1≤a,b≤104). We paint all the numbers in increasing number first we paint 0, then we paint 1, then 2 and so on.
Each number is painted white or black. We paint a number i according to the following rules:
if i=0, it is colored white;
if i≥a and i−a is colored white, i is also colored white;
if i≥b and i−b is colored white, i is also colored white;
if i is still not colored white, it is colored black.
In this way, each nonnegative integer gets one of two colors.
For example, if a=3, b=5, then the colors of the numbers (in the order from 0) are: white (0), black (1), black (2), white (3), black (4), white (5), white (6), black (7), white (8), white (9), …
Note that:
It is possible that there are infinitely many nonnegative integers colored black. For example, if a=10 and b=10, then only 0,10,20,30 and any other nonnegative integers that end in 0 when written in base 10 are white. The other integers are colored black.
It is also possible that there are only finitely many nonnegative integers colored black. For example, when a=1 and b=10, then there is no nonnegative integer colored black at all.
Your task is to determine whether or not the number of nonnegative integers colored black is infinite.
If there are infinitely many nonnegative integers colored black, simply print a line containing “Infinite” (without the quotes). Otherwise, print “Finite” (without the quotes).
输入:
The first line of input contains a single integer t (1≤t≤100) — the number of test cases in the input. Then t lines follow, each line contains two space-separated integers a and b (1≤a,b≤104).
输出:
For each test case, print one line containing either “Infinite” or “Finite” (without the quotes). Output is case-insensitive (i.e. “infinite”, “inFiNite” or “finiTE” are all valid answers).
样例输入:
4
10 10
1 10
6 9
7 3
样例输出:
Infinite
Finite
Infinite
Finite
解题思路:
这题刚开始写的时候我根本毫无头绪,但是我看到6 9,真的是灵光一现,我觉得应该是有公因数或者两个数相等,就无限,否则就有限,我就抱着试试的心态,居然对了。嘻嘻,运气真好,虽然我现在还是不知道它的原因。
程序代码:
#include2.Restricted RPS
题意:
Let n be a positive integer. Let a,b,c be nonnegative integers such that a+b+c=n.
Alice and Bob are gonna play rock-paper-scissors n times. Alice knows the sequences of hands that Bob will play. However, Alice has to play rock a times, paper b times, and scissors c times.
Alice wins if she beats Bob in at least ⌈n2⌉ (n2 rounded up to the nearest integer) hands, otherwise Alice loses.
Note that in rock-paper-scissors:
rock beats scissors;
paper beats rock;
scissors beat paper.
The task is, given the sequence of hands that Bob will play, and the numbers a,b,c, determine whether or not Alice can win. And if so, find any possible sequence of hands that Alice can use to win.
If there are multiple answers, print any of them.
输入:
The first line contains a single integer t (1≤t≤100) — the number of test cases.
Then, t testcases follow, each consisting of three lines:
The first line contains a single integer n (1≤n≤100).
The second line contains three integers, a,b,c (0≤a,b,c≤n). It is guaranteed that a+b+c=n.
The third line contains a string s of length n. s is made up of only ‘R’, ‘P’, and ‘S’. The i-th character is ‘R’ if for his i-th Bob plays rock, ‘P’ if paper, and ‘S’ if scissors.
输出:
For each testcase:
If Alice cannot win, print “NO” (without the quotes).
Otherwise, print “YES” (without the quotes). Also, print a string t of length n made up of only ‘R’, ‘P’, and ‘S’ — a sequence of hands that Alice can use to win. t must contain exactly a 'R’s, b 'P’s, and c 'S’s.
If there are multiple answers, print any of them.
The “YES” / “NO” part of the output is case-insensitive (i.e. “yEs”, “no” or “YEs” are all valid answers). Note that ‘R’, ‘P’ and ‘S’ are case-sensitive.
样例输入:
2
3
1 1 1
RPS
3
3 0 0
RPS
样例输出:
YES
PSR
NO
注意:
In the first testcase, in the first hand, Alice plays paper and Bob plays rock, so Alice beats Bob. In the second hand, Alice plays scissors and Bob plays paper, so Alice beats Bob. In the third hand, Alice plays rock and Bob plays scissors, so Alice beats Bob. Alice beat Bob 3 times, and 3≥⌈32⌉=2, so Alice wins.
In the second testcase, the only sequence of hands that Alice can play is “RRR”. Alice beats Bob only in the last hand, so Alice can’t win. 1<⌈32⌉=2.
解题思路:
就是知道对方的出拳顺序,让你判断你能不能赢,只要赢一半就行了。
刚开始忘了判断如果输了怎么出拳,最后才想到,加了判断就对了。
程序代码:
#include
int len1=s1.length();
int cnt=0;
int cnt1=0;
char ans[100+5];
for(int i=0;i<len1;i++){
if(s1[i]=='R'){
if(b>=1){
b--;
ans[cnt++]='P';
cnt1++;
}else{
ans[cnt++]='k';
}
}else if(s1[i]=='P'){
if(c>=1){
c--;
ans[cnt++]='S';
cnt1++;
}else{
ans[cnt++]='k';
}
}else if(s1[i]=='S'){
if(a>=1){
a--;
ans[cnt++]='R';
cnt1++;
}else{
ans[cnt++]='k';
}
}
}
int nn;
if(n%2==0){
nn=n/2;
}else{
nn=n/2+1;
}
if(cnt1>=nn){
printf("YES\n");
for(int i=0;i<n;i++){
if(ans[i]=='R')
a1--;
else if(ans[i]=='S')
c1--;
else if(ans[i]=='P')
b1--;
}
for(int i=0;i<n;i++){
if(ans[i]=='k'){
if(a1){
printf("%c",'R');
a1--;
}else if(b1){
printf("%c",'P');
b1--;
}else if(c1){
printf("%c",'S');
c1--;
}
}else{
printf("%c",ans[i]);
}
}
printf("\n");
}else{
printf("NO\n");
}
}
return 0;
}
二、Atcoder
1. ><
题意:
Given is a string S of length N−1. Each character in S is < or >.
A sequence of N non-negative integers, a1,a2,⋯,aN, is said to be good when the following condition is satisfied for all i (1≤i≤N−1):
If Si= <: ai
Find the minimum possible sum of the elements of a good sequence of N non-negative integers.
2≤N≤5×10^5
S is a string of length N−1 consisting of < and >.
输入:
Input is given from Standard Input in the following format:
S
输出:
Find the minimum possible sum of the elements of a good sequence of N non-negative integers.
样例输入:
<>>
样例输出:
3
a=(0,2,1,0) is a good sequence whose sum is 3. There is no good sequence whose sum is less than 3.
样例输入:
<>>><<><<<<<>>><
样例输出:
28
解题思路:
就是让你填数然后问你最小的和是多少。当天晚上比赛的时候我写出来了,但是后面一半的测试点都错了!!我改了好久都没对,最后我就睡了。第二天我看了别人的代码,看到她用了long long ,我把自己的代码改成long long,居然过了!!!啊啊啊啊啊!!好让人生气啊!!!!
程序代码:
#include三、Wlacm
1.牛的旅行
题意:
农民John的农场里有很多牧区。有的路径连接一些特定的牧区。一片所有连通的牧区称为一个牧场。但是就目前而言,你能看到至少有两个牧区不连通。现在,John想在农场里添加一条路径 ( 注意,恰好一条 )。对这条路径有这样的限制:一个牧场的直径就是牧场中最远的两个牧区的距离 ( 本题中所提到的所有距离指的都是最短的距离 )。考虑如下的两个牧场,图1是有5个牧区的牧场,牧区用“*”表示,路径用直线表示。每一个牧区都有自己的坐标:
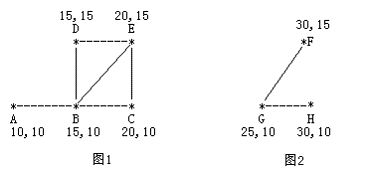
图1所示的牧场的直径大约是12.07106, 最远的两个牧区是A和E,它们之间的最短路径是A-B-E。 这两个牧场都在John的农场上。John将会在两个牧场中各选一个牧区,然后用一条路径连起来,使得连通后这个新的更大的牧场有最小的直径。注意,如果两条路径中途相交,我们不认为它们是连通的。只有两条路径在同一个牧区相交,我们才认为它们是连通的。 现在请你编程找出一条连接两个不同牧场的路径,使得连上这条路径后,这个更大的新牧场有最小的直径。
输入:
第 1 行:一个整数N (1 <= N <= 150), 表示牧区数; 第 2 到 N+1 行:每行两个整数X,Y ( 0 <= X,Y<= 100000 ), 表示N个牧区的坐标。每个牧区的坐标都是不一样的。第 N+2 行到第 2*N+1 行:每行包括N个数字 ( 0或1 ) 表示一个对称邻接矩阵。 例如,题目描述中的两个牧场的矩阵描述如下:
A B C D E F G H
A 0 1 0 0 0 0 0 0
B 1 0 1 1 1 0 0 0
C 0 1 0 0 1 0 0 0
D 0 1 0 0 1 0 0 0
E 0 1 1 1 0 0 0 0
F 0 0 0 0 0 0 1 0
G 0 0 0 0 0 1 0 1
H 0 0 0 0 0 0 1 0
输入数据中至少包括两个不连通的牧区。
输出:
只有一行,包括一个实数,表示所求答案。数字保留六位小数。
样例输入:
8
10 10
15 10
20 10
15 15
20 15
30 15
25 10
30 10
01000000
10111000
01001000
01001000
01110000
00000010
00000101
00000010
样例输出:
22.071068
解题思路:
先用Floyd求一遍最短路,然后再求每个点和最远点的距离,最后枚举两个不连通的点,然后就可以计算新的牧区的直径,最后求最大值就行了。但是我用字符读入01串居然是错的,后来改成整数读入就对了,真奇怪。
程序代码:
#include
// g[i][j]=t;
// }
}else if(i!=j){
g[i][j]=INF;
}
// if(i==j){
// g[i][j]=0;
// }
}
// getchar();
}
for(int k=1;k<=n;k++){ //Floyd求一遍最短路径
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(g[i][k]+g[k][j]<g[i][j])
g[i][j]=g[i][k]+g[k][j];
}
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(g[i][j]!=INF){ //求每一个点距离它最远的点的距离
gg[i]=max(g[i][j],gg[i]);
}
L=max(L,gg[i]); //这个是牧区目前的最大直径
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(g[i][j]==INF){
L1=min(gg[i]+cal(i,j)+gg[j],L1); //枚举两个不连通的点,然后就可以计算新的牧区的直径
}
}
}
ans=max(L,L1); //因为有可能新联通的牧场还没有原来的牧场大,所以还要再取一遍最大值
printf("%.6f\n",ans);
return 0;
}
2.香甜的黄油
题意:
农夫John发现做出全威斯康辛州最甜的黄油的方法:糖。把糖放在一片牧场上,他知道N(1<=N<=500)只奶牛会过来舔它,这样就能做出能卖好价钱的超甜黄油。当然,他将付出额外的费用在奶牛上。
农夫John很狡猾。像以前的巴甫洛夫,他知道他可以训练这些奶牛,让它们在听到铃声时去一个特定的牧场。他打算将糖放在那里然后下午发出铃声,以至他可以在晚上挤奶。
农夫John知道每只奶牛都在各自喜欢的牧场(一个牧场不一定只有一头牛)。给出各头牛在的牧场和牧场间的路线,找出使所有牛到达的路程和最短的牧场(他将把糖放在那)。
输入:
第一行: 三个数:奶牛数N,牧场数P(2<=P<=800),牧场间道路数C(1<=C<=1450)。
第二行到第N+1行: 1到N头奶牛所在的牧场号。
第N+2行到第N+C+1行:每行有三个数:相连的牧场A、B,两牧场间距(1<=D<=255),当然,连接是双向的。
输出:
一行 输出奶牛必须行走的最小的距离和.
样例输入:
3 4 5
2
3
4
1 2 1
1 3 5
2 3 7
2 4 3
3 4 5
样例输出:
8
提示:
解题思路:
这题本来看数据应该不能用Floyd的,但是我看到网上有人说因为是双向边,所以只用算一半就可以了,我就用了Floyd,嘻嘻,还是Floyd最简单,最好用。用Floyd,数组初始化,建议还是手动初始化。
程序代码:
#include四、Vjudge
1.find the mincost route
题意:
杭州有N个景区,景区之间有一些双向的路来连接,现在8600想找一条旅游路线,这个路线从A点出发并且最后回到A点,假设经过的路线为V1,V2,…VK,V1,那么必须满足K>2,就是说至除了出发点以外至少要经过2个其他不同的景区,而且不能重复经过同一个景区。现在8600需要你帮他找一条这样的路线,并且花费越少越好。
输入:
第一行是2个整数N和M(N <= 100, M <= 1000),代表景区的个数和道路的条数。
接下来的M行里,每行包括3个整数a,b,c.代表a和b之间有一条通路,并且需要花费c元(c <= 100)。
输出:
对于每个测试实例,如果能找到这样一条路线的话,输出花费的最小值。如果找不到的话,输出"It’s impossible.".
样例输入:
3 3
1 2 1
2 3 1
1 3 1
3 3
1 2 1
1 2 3
2 3 1
样例输出:
3
It's impossible.
解题思路:
其实就是最短路,用floyd走一遍,只不过因为最后要走回来,所以最后还要加上最后一个点到第一个点的距离,然后求最小值就行了。但是我写的一直出错!!!我觉得我都把自己的代码,改的快和AC的代码一样了,就是不知道哪里错了真让人生气!!
程序代码:(WA)
#include程序代码:(AC)
#include