sklearn之样本生成
机器学习、模式识别的目的就是从样本数据上自动建立数学模型,将模型用于新的数据以自动解决实际问题。因此,这里有两个东西是我们比较关心的,一个是模型,另外一个样本数据。现在很多文章都在讨论各种算法,大都可以归为模型的建立过程,今天,本博文讲另外一个重要组成部分,样本数据获取方法(以sklearn为工具)。
通过Sklearn获取的样本数据格式有三种形式:
①图像样本格式
②样本数据自主生成格式和svmlight加载格式
③Toy 数据集格式、现实世界使用格式和从mldata.org获取的格式
1、toy 数据集
由一些小批量经典数据集组成,无需通过网络下载,直接可以加载使用,非常方便。
API接口如下表所示:
load_boston([return_X_y]) #加载波士顿房价数据;用于回归问题
load_iris([return_X_y]) #加载iris 数据集;用于分类问题
load_diabetes([return_X_y]) #加载糖尿病数据集;用于回归问题
load_digits([n_class, return_X_y]) #加载手写字符集;用于分类问题
load_linnerud([return_X_y]) #加载linnerud 数据集;用于多元回归问题 这些数据集可用于快速验证算法性能,但是由于数据集较小,所得结论并不一定适用于现实条件。
1.1 返回数据格式返回一个字典格式数据,其中至少包含两个键值:data数据(n_samples*n_features),target数据。
1.2 示例代码
对于digits数据集:
#加载数据集,显示0
from sklearn.datasets import load_digits
digits = load_digits()
data=digits.data
import matplotlib.pyplot as plt
#plt.gray()
#plt.imshow(digits.images[0])
plt.matshow(digits.images[0])
plt.show()load_sample_images()
加载图像用于图形处理(仅有两幅图)
load_sample_image(image_name)
加载numpy格式的图像数据
2.1 示例代码
from sklearn.datasets import load_sample_image
img=load_sample_image('flower.jpg')
import matplotlib.pyplot as plt
plt.imshow(img)
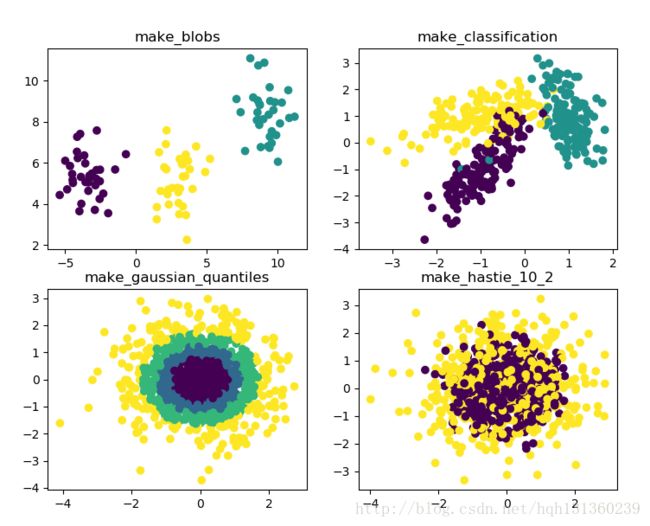
plt.show() 1、make_blobs
import sklearn.datasets
import matplotlib.pyplot as plt
X1, Y1=sklearn.datasets.make_blobs(n_samples=100, n_features=2,centers=3)
plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1)
plt.show()n_samples 是待生成的样本的总数。
n_features 是每个样本的特征数。
centers 表示类别数。
cluster_std表示每个类别的方差,
例如我们希望生成2类数据,其中一类比另一类具有更大的方差,可以将cluster_std设置为[1.0,3.0]。
2、make_classification
sklearn.datasets.make_classification(n_samples=100, n_features=20, n_informative=2, n_redundant=2,
n_repeated=0, n_classes=2, n_clusters_per_class=2, weights=None,
flip_y=0.01, class_sep=1.0, hypercube=True,shift=0.0, scale=1.0,
shuffle=True, random_state=None) n_features :特征个数
n_informative:多信息特征的个数
n_redundant:冗余信息,informative特征的随机线性组合
n_repeated :重复信息,随机提取n_informative和n_redundant 特征
n_classes:分类类别
n_clusters_per_class :某一个类别是由几个cluster构成的
random_state : 确定每次生成的数据都一致
这里我们用make_classification生成三元分类模型数据。几个关键参数有n_samples(生成样本数), n_features(样本特征数), n_redundant(冗余特征数)和n_classes(输出的类别数),例子代码如下:
#coding:utf-8
import sklearn.datasets
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
# X1为样本特征,Y1为样本类别输出, 共400个样本,每个样本2个特征,输出有3个类别,没有冗余特征,每个类别一个簇
X1, Y1 = make_classification(n_samples=400, n_features=2, n_redundant=0,
n_clusters_per_class=1, n_classes=3)
plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1)
plt.show()3、make_gaussian_quantiles和make_hastie_10_2
sklearn.datasets.make_gaussian_quantiles(mean=None, cov=1.0, n_samples=100, n_features=2, n_classes=3,
shuffle=True, random_state=None) ②利用Hastie算法,生成2分类数据
#coding:utf-8
import matplotlib.pyplot as plt
from sklearn.datasets import make_gaussian_quantiles
from sklearn.datasets import make_hastie_10_2
X1, Y1 = make_gaussian_quantiles(n_samples=1000,n_features=2, n_classes=4)
plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1)
plt.show()
X1, Y1 = make_hastie_10_2(n_samples=1000)
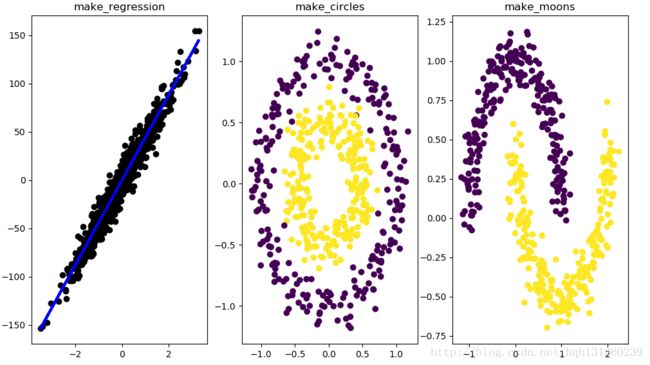
plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1) 4、make_regression
(回归模型随机数据)
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
# X为样本特征,y为样本输出, coef为回归系数,共1000个样本,每个样本1个特征
X, y, coef =make_regression(n_samples=1000, n_features=1,noise=10, coef=True)
# 画图
plt.scatter(X, y, color='black')
plt.plot(X, X*coef, color='blue',linewidth=3)
plt.show()
5、make_circles和make_moons
sklearn.datasets.make_circles(n_samples=100, shuffle=True, noise=None, random_state=None, factor=0.8)
sklearn.datasets.make_moons(n_samples=100, shuffle=True, noise=None, random_state=None)
生成环形数据(2个圈)
factor :外圈与内圈的尺度因子<1
生成半环形图(2个半圈)
factor :外圈与内圈的尺度因子<1
生成半环形图(2个半圈)
from sklearn.datasets import make_circles
from sklearn.datasets import make_moons
import matplotlib.pyplot as plt
import numpy as np
## 分成1x2,占用第一个,即第一行第一列的子图
plt.subplot(121)
x1,y1=make_circles(n_samples=500,factor=0.5,noise=0.1)
plt.scatter(x1[:,0],x1[:,1],marker='o',c=y1)
plt.subplot(122)
x1,y1=make_moons(n_samples=500,noise=0.1)
plt.scatter(x1[:,0],x1[:,1],marker='o',c=y1)
plt.show()