Dijkstra迪科斯彻算法



主要参考《算法导论》与维基百科。

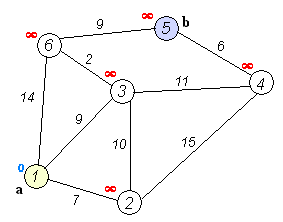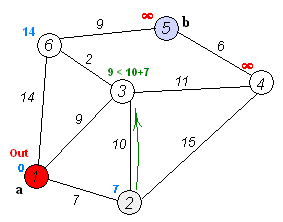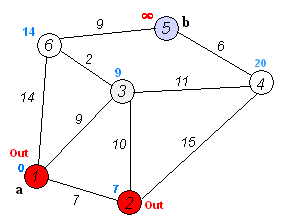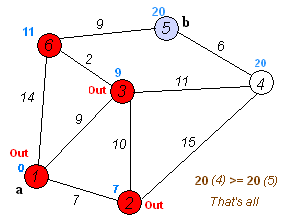
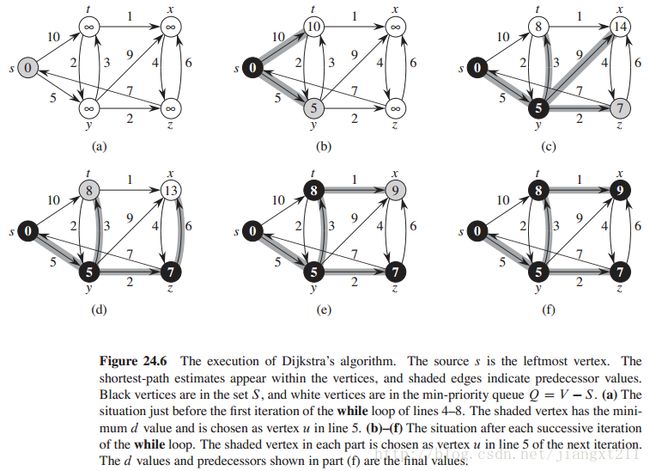
戴克斯特拉算法（英语：Dijkstra's algorithm）是由荷兰计算机科学家艾兹赫尔·戴克斯特拉提出。迪科斯彻算法使用了广度优先搜索解决非负权有向图的单源最短路径问题，算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。举例来说，如果图中的顶点表示城市，而边上的权重表示著城市间开车行经的距离，该算法可以用来找到两个城市之间的最短路径。（摘录自维基百科）

Dijkstra算法解决了有向图G=（V，S)上带权重的单源最短路径问题，它要求所有边的权重为非负值。Dijkstra算法在运行过程中维持的关键信息是一组结点的结合S。从源节点s到该集合中每个结点之间的最短路径已经被找到。算法重复从结点集V-S中选择最短路径估计最小的结点u，将u加入到集合S，然后对所有从u发出的边进行松弛。

//=====================================================
// Dijkstra算法实现
//=====================================================
#include 
#include 

#define INFINITE 0xff
#define VERTEXS 5
#define EDGES 10

int G[VERTEXS][VERTEXS] = {
//  s   t   x   y   z
    INFINITE,  10, INFINITE,  5,  INFINITE, // s
    INFINITE,  INFINITE,  1,  2,  INFINITE, // t
    INFINITE,  INFINITE,  INFINITE,  INFINITE,  4, // x
    INFINITE,  3,  9,  INFINITE,  2, // y
    7,  INFINITE,  6,  INFINITE,  INFINITE  // z
};

char vs[VERTEXS] = {'s', 't', 'x', 'y', 'z'};
int dis[VERTEXS] = {0}; // 记录源点到目的点的距离
bool visited[VERTEXS] = {false};
int prev[VERTEXS] = {0};

//=================================================
// 获取Q中最小元素
//=================================================
int ExtractMin(int *Q, int n)
{
	int min = INFINITE;
	int index = -1;
	for (int i = 0; i < n; i++) {
		if (!visited[i] && Q[i] < min) {
			min = Q[i];
			index = i;  // 获取最小元素的小标
		}
	}
	if (index > -1)
		visited[index] = true;

	return index;
}

//=================================================
// 判断Q是否为空
//=================================================
bool IsEmpty(int *Q, int n)
{
	for (int i = 0; i < n; i++) {
		if (!visited[i])
			return true;
	}

	return false;
}

//=================================================
// 对边(u, v)进行松弛操作
//=================================================
void Relax(int u, int v, int w)
{
	if (dis[v] > dis[u] + w) {
		dis[v] = dis[u] + w;
		prev[v] = u;
	}
}

void Dijkstra(/*int **G, int w, */int s)
{
	for (int i = 0; i < VERTEXS; i++) { // 初始化
		dis[i] = INFINITE;
		visited[i] = false;
		prev[i] = 0;
	}

	dis[s] = 0; // 起始点
	while (IsEmpty(dis, VERTEXS)) {
		int u = ExtractMin(dis, VERTEXS);
		for (int v = 0; v < VERTEXS; v++) {
			if (G[u][v] < INFINITE) { // 边存在
				Relax(u, v, G[u][v]);
			}
		}
	}
}

//================================================
// 打印d-->s
//================================================
void PrintPath(int s, int d)
{
	while (d != s) {
		printf("%d-->",d);
		d = prev[d];
	}
	printf("%d\n", s);
}

//================================================
// 递归打印s-->d
//================================================
void PrintPath1(int s, int d)
{
	if (s != d) 
		PrintPath1(s, prev[d]);
	printf("%d-->", d);
}

int main()
{
	int s = 0;
	Dijkstra(s);

	for (int i = 1; i < VERTEXS; i++) {
		printf("%d->%d: ", s, i);
		PrintPath(s, i);
// 		PrintPath1(s, i);
// 		printf("\n");
	}

	system("pause");
	return 0;
}