jupyter中使用matplotlib

小试牛刀

matplotlib可能是Python 2D绘图领域使用最广泛的库了。它能够让使用者轻松地将数据图形化，并且提供多样化的输出格式。同时，它几乎能够对图进行所有你能够想到的细节的修饰。

我们先来看看一个小例子：

In [1]:

%matplotlib inline
import matplotlib.pyplot as plt # 导入绘图包
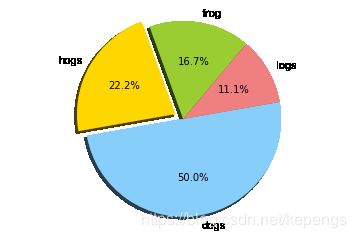
labels = 'frog', 'hogs', 'dogs', 'logs' # 设定数据标签
sizes = 15, 20, 45, 10 # 设定数据
colors = 'yellowgreen', 'gold', 'lightskyblue', 'lightcoral' # 设定颜色
explode = 0, 0.1, 0, 0
plt.pie(sizes, explode=explode, labels=labels, colors=colors, autopct='%1.1f%%', shadow=True, startangle=50)
plt.axis('equal')
plt.show()

显示中文

matplotlib默认绘图并不支持中文，因此如果我们的图中需要有中文，那么我们必须进行一点设置：

In [2]:

import matplotlib as mpl  
mpl.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签  
mpl.rcParams['axes.unicode_minus']=False #用来正常显示负号 

函数式绘图

实际上，matplotlib是受MATLAB的启发构建的。MATLAB是数据绘图领域广泛使用的语言和工具。MATLAB语言是面向过程的(相对于面向对象)。利用函数调用，MATLAB可以轻松地进行数据图形的绘制。
matplotlib有一套完全仿照MATLAB的函数形式的绘图接口，由 matplotlib.pyplot 模块提供。虽然matplotlib的实现还是面向对象，但一般用户只需要使用 matplotlib.pyplot 就可以完成数据图形绘制，不过如果涉及到一些特别细节的调整就不得不去直接调整matplotlib实现的对象了。

为项目设置matplotlib参数

我们有两种方法修改参数：

• 使用参数字典 rcParams，就像上面我们想要正常显示中文和负号进行的参数设置
• 调用matplotlib.rc()命令，通过传入关键字元组来修改参数

比较常见的配置项有：

• axis：设置坐标轴边界和表面的颜色、坐标刻度值大小和网格的显示
• figure: 控制dpi、边界颜色、图形大小、和子区( subplot)设置
• font: 字体集（font family）、字体大小和样式设置
• grid: 设置网格颜色和线性
• legend: 设置图例和其中的文本的显示
• line: 设置线条（颜色、线型、宽度等）和标记
• patch: 是填充2D空间的图形对象，如多边形和圆。控制线宽、颜色和抗锯齿设置等。
• savefig: 可以对保存的图形进行单独设置。例如，设置渲染的文件的背景为白色。
• verbose: 设置matplotlib在执行期间信息输出，如silent、helpful、debug和debug-annoying。
• xticks和yticks: 为x,y轴的主刻度和次刻度设置颜色、大小、方向，以及标签大小。

实际上对于这些，我们不需要背下来，当有相应的需求再去查询文档或者搜索答案即可。
这里只是为了让你知道在matplotlib里有这种能力。而且，默认的这些配置基本上已经能够满足我们的使用，更改它们的情况非常少。

一个例子

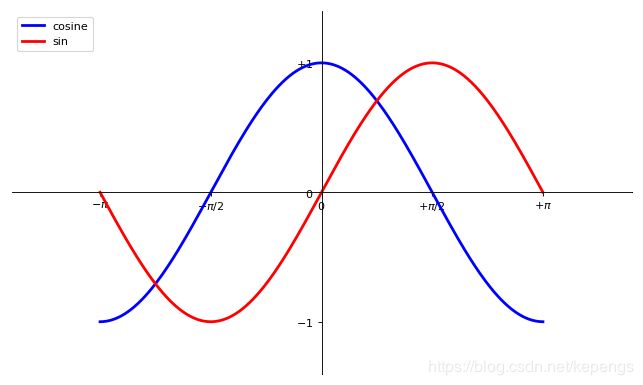
这一节，我们将从简到繁：先尝试用默认配置在同一张图上绘制正弦和余弦函数图像，然后逐步美化它。

让我们先生成正弦和余弦函数的一些值：

In [3]:

import numpy as np

# 从 −π−π 到 +π+π 等间隔的 256 个值
X = np.linspace(-np.pi, np.pi, 256, endpoint=True)
C, S = np.cos(X), np.sin(X)

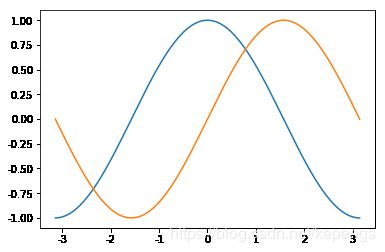
默认配置绘图

In [4]:

plt.plot(X,C)
plt.plot(X,S)
plt.show()

/Users/sunkepeng/anaconda2/lib/python2.7/site-packages/matplotlib/font_manager.py:1331: UserWarning: findfont: Font family [u'sans-serif'] not found. Falling back to DejaVu Sans
  (prop.get_family(), self.defaultFamily[fontext]))

默认配置的具体内容

下面的代码中，我们展现了 matplotlib 的默认配置并辅以注释说明，这部分配置包含了有关绘图样式的所有配置。代码中的配置与默认配置几乎相同，你可以在交互模式中修改其中的值来观察效果。

In [5]:

# 创建一个8 * 6点(point)的图，并设置分辨率为80
plt.figure(figsize=(8, 6), dpi=80)

# 创建一个新的 1 * 1的子图，接下来的图样绘制在其中的第 1 块（也是唯一的一块）
plt.subplot(1,1,1)

# 绘制余弦曲线，使用蓝色的、连续的、宽度为 1 （像素）的线条
plt.plot(X, C, color="blue", linewidth=1.0, linestyle="-")
# 绘制正弦曲线，使用绿色的、连续的、宽度为 1 （像素）的线条
plt.plot(X, S, color="green", linewidth=1.0, linestyle="-")

# 设置横轴的上下限
plt.xlim(-4.0,4.0)
# 设置横轴坐标点
plt.xticks(np.linspace(-4,4,9,endpoint=True))

# 设置纵轴的上下限
plt.ylim(-1.0,1.0)
# 设置纵轴坐标点
plt.yticks(np.linspace(-1,1,5,endpoint=True))

# 在屏幕上显示
plt.show()

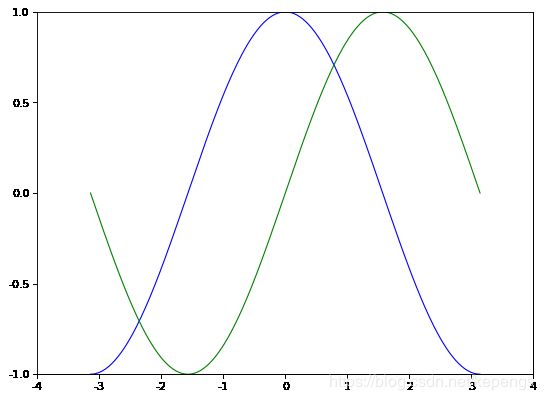
改变线条的颜色和粗细

首先，我们以蓝色和红色分别表示余弦和正弦函数，而后将线条变粗一点。接下来，我们在水平方向拉伸一下整个图。

In [6]:

plt.figure(figsize=(10,6), dpi=80) # 水平方向拉伸

plt.xlim(-4.0,4.0)
plt.xticks(np.linspace(-4,4,9,endpoint=True))
plt.ylim(-1.0,1.0)
plt.yticks(np.linspace(-1,1,5,endpoint=True))

plt.plot(X, C, color='blue', linewidth=2.5, linestyle='-') # 余弦曲线使用蓝色，并将线宽设置为2.5，采用实线绘制
plt.plot(X, S, color="red",  linewidth=2.5, linestyle="-") # # 正弦曲线使用红色，并将线宽设置为2.5，采用实线绘制
plt.show()

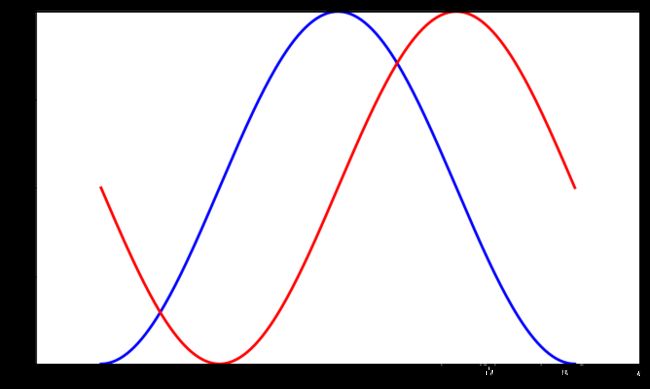
设置图片边界

当前的图片边界设置得不好，所以有些地方看得不是很清楚。

In [7]:

plt.figure(figsize=(10,6), dpi=80) # 水平方向拉伸

# 坐标的设置
xmin ,xmax = X.min(), X.max()
ymin, ymax = C.min(), C.max()

dx = (xmax - xmin) * 0.2
dy = (ymax - ymin) * 0.2

plt.xlim(xmin - dx, xmax + dx)
plt.ylim(ymin - dy, ymax + dy)

plt.plot(X, C, color='blue', linewidth=2.5, linestyle='-') # 余弦曲线使用蓝色，并将线宽设置为2.5，采用实线绘制
plt.plot(X, S, color="red",  linewidth=2.5, linestyle="-") # # 正弦曲线使用红色，并将线宽设置为2.5，采用实线绘制
plt.show()

设置坐标点

我们讨论正弦和余弦函数的时候，通常希望知道函数在 ±π±π 和 ±π2±π2 的值。这样看来，当前的设置就不那么理想了。

In [8]:

plt.figure(figsize=(10,6), dpi=80)

xmin ,xmax = X.min(), X.max()
ymin, ymax = C.min(), C.max()

dx = (xmax - xmin) * 0.2
dy = (ymax - ymin) * 0.2

plt.xlim(xmin - dx, xmax + dx)
plt.ylim(ymin - dy, ymax + dy)

plt.xticks( [-np.pi, -np.pi/2, 0, np.pi/2, np.pi]) # 设置x轴坐标点
plt.yticks([-1, 0, +1]) # 设置y轴坐标点

plt.plot(X, C, color='blue', linewidth=2.5, linestyle='-')
plt.plot(X, S, color="red",  linewidth=2.5, linestyle="-")
plt.show()

设置轴坐标点的标签

轴坐标点现在没问题了，不过标签却不大符合期望。我们可以把 3.142 当做是 π，但毕竟不够精确。当我们设置记号的时候，我们可以同时设置记号的标签。注意这里使用了 LaTeX。

In [9]:

plt.figure(figsize=(10,6), dpi=80)

xmin ,xmax = X.min(), X.max()
ymin, ymax = C.min(), C.max()

dx = (xmax - xmin) * 0.2
dy = (ymax - ymin) * 0.2

plt.xlim(xmin - dx, xmax + dx)
plt.ylim(ymin - dy, ymax + dy)

plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
       [r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$']) # 设置x轴坐标点及其显示标签

plt.yticks([-1, 0, +1],
       [r'$-1$', r'$0$', r'$+1$']) # 设置y轴坐标点及其显示标签

plt.plot(X, C, color='blue', linewidth=2.5, linestyle='-')
plt.plot(X, S, color="red",  linewidth=2.5, linestyle="-")
plt.show()

移动脊柱(spines)

坐标轴线和上面的记号连在一起就形成了脊柱（Spines），它记录了数据区域的范围。它们可以放在任意位置，不过至今为止，我们都把它放在图的四边。

实际上每幅图有四条脊柱（上下左右），为了将脊柱放在图的中间，我们必须将其中的两条（上和右）设置为无色，然后调整剩下的两条到合适的位置——数据空间的 0 点。

In [10]:

plt.figure(figsize=(10,6), dpi=80)
xmin ,xmax = X.min(), X.max()
ymin, ymax = C.min(), C.max()
dx = (xmax - xmin) * 0.2
dy = (ymax - ymin) * 0.2
plt.xlim(xmin - dx, xmax + dx)
plt.ylim(ymin - dy, ymax + dy)
plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
       [r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$'])
plt.yticks([-1, 0, +1],
       [r'$-1$', r'$0$', r'$+1$'])

ax = plt.gca()
ax.spines['right'].set_color('none') # 右侧侧不显示
ax.spines['top'].set_color('none') # 上侧不显示
ax.xaxis.set_ticks_position('bottom') # 设置坐标点在轴下侧
ax.spines['bottom'].set_position(('data',0)) # 设置底部轴位置
ax.yaxis.set_ticks_position('left') # 设置坐标点在轴左侧
ax.spines['left'].set_position(('data',0)) # 设置左侧轴位置


plt.plot(X, C, color='blue', linewidth=2.5, linestyle='-', label='cosine') # 增加了label以便增加图例
plt.plot(X, S, color="red",  linewidth=2.5, linestyle="-", label='sin') # 增加了label以便增加图例
plt.legend(loc='upper left') # 顺便添加个图例

plt.show()

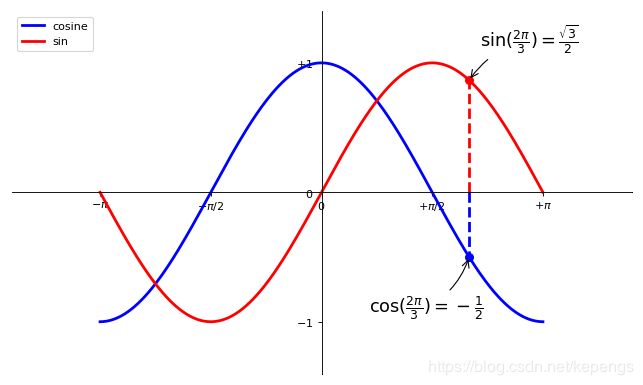
增加注释

我们希望在 2π/3 的位置给两条函数曲线加上一个注释。首先，我们在对应的函数图像位置上画一个点；然后，向横轴引一条垂线，以虚线标记；最后，写上注释。

In [11]:

plt.figure(figsize=(10,6), dpi=80)
xmin ,xmax = X.min(), X.max()
ymin, ymax = C.min(), C.max()
dx = (xmax - xmin) * 0.2
dy = (ymax - ymin) * 0.2
plt.xlim(xmin - dx, xmax + dx)
plt.ylim(ymin - dy, ymax + dy)
plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
       [r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$'])
plt.yticks([-1, 0, +1],
       [r'$-1$', r'$0$', r'$+1$'])

ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))

plt.plot(X, C, color='blue', linewidth=2.5, linestyle='-', label='cosine')
plt.plot(X, S, color="red",  linewidth=2.5, linestyle="-", label='sin')
plt.legend(loc='upper left')


t = 2*np.pi/3 # 2π/3
plt.plot([t,t],[0,np.cos(t)], color ='blue', linewidth=2.5, linestyle="--") # 余弦的垂线
plt.scatter([t,],[np.cos(t),], 50, color ='blue') # 余弦的标注点(只有一个点的散点图)
plt.annotate(r'$\cos(\frac{2\pi}{3})=-\frac{1}{2}$',
         xy=(t, np.cos(t)), xycoords='data',
         xytext=(-90, -50), textcoords='offset points', fontsize=16,
         arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2")) # 为余弦注释点写注释


plt.plot([t,t],[0,np.sin(t)], color ='red', linewidth=2.5, linestyle="--") # 正弦的垂线
plt.scatter([t,],[np.sin(t),], 50, color ='red') # 正弦的标注点(只有一个点的散点图)
plt.annotate(r'$\sin(\frac{2\pi}{3})=\frac{\sqrt{3}}{2}$',
         xy=(t, np.sin(t)), xycoords='data',
         xytext=(+10, +30), textcoords='offset points', fontsize=16,
         arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2")) # 为正弦注释点写注释


plt.show()

至此，我们的这个小例子就结束了。希望大家能够通过这个例子大略上了解matplotlib的能力。

可以这么说，在数据绘图方面，几乎任何你见过的东西都可以使用它绘制出来，当你需要使用的时候可以现查文档。

当然，你也可以留着这份notebook，常用的东西差不多都在这里了。

其他类型的图

这部分我们大略地显示一下其他类型的图作为对于matplotlib介绍的收尾。

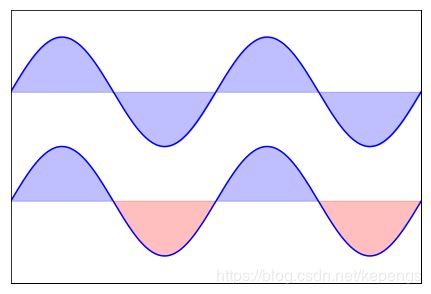
普通图

In [12]:

n = 256
X = np.linspace(-np.pi,np.pi,n,endpoint=True)
Y = np.sin(2*X)

plt.axes([0.025,0.025,0.95,0.95])

plt.plot (X, Y+1, color='blue', alpha=1.00)
plt.fill_between(X, 1, Y+1, color='blue', alpha=.25)

plt.plot (X, Y-1, color='blue', alpha=1.00)
plt.fill_between(X, -1, Y-1, (Y-1) > -1, color='blue', alpha=.25)
plt.fill_between(X, -1, Y-1, (Y-1) < -1, color='red',  alpha=.25)

plt.xlim(-np.pi,np.pi), plt.xticks([])
plt.ylim(-2.5,2.5), plt.yticks([])
# plt.savefig('../figures/plot_ex.png',dpi=48) # 我都忘了介绍存储图的方法了
plt.show()

散点图

In [13]:

n = 1024
X = np.random.normal(0,1,n)
Y = np.random.normal(0,1,n)
T = np.arctan2(Y,X)

plt.axes([0.025,0.025,0.95,0.95])
plt.scatter(X,Y, s=75, c=T, alpha=.5)

plt.xlim(-1.5,1.5), plt.xticks([])
plt.ylim(-1.5,1.5), plt.yticks([])
# savefig('../figures/scatter_ex.png',dpi=48)
plt.show()

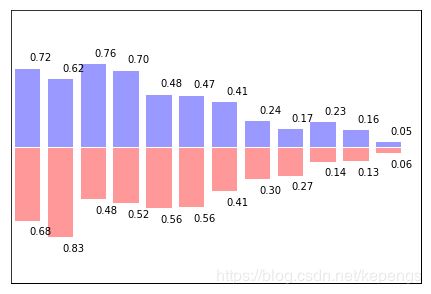
条形图

In [14]:

n = 12
X = np.arange(n)
Y1 = (1-X/float(n)) * np.random.uniform(0.5,1.0,n)
Y2 = (1-X/float(n)) * np.random.uniform(0.5,1.0,n)

plt.axes([0.025,0.025,0.95,0.95])
plt.bar(X, +Y1, facecolor='#9999ff', edgecolor='white')
plt.bar(X, -Y2, facecolor='#ff9999', edgecolor='white')

for x,y in zip(X,Y1):
    plt.text(x+0.4, y+0.05, '%.2f' % y, ha='center', va= 'bottom')

for x,y in zip(X,Y2):
    plt.text(x+0.4, -y-0.05, '%.2f' % y, ha='center', va= 'top')

plt.xlim(-.5,n), plt.xticks([])
plt.ylim(-1.25,+1.25), plt.yticks([])

# savefig('../figures/bar_ex.png', dpi=48)
plt.show()

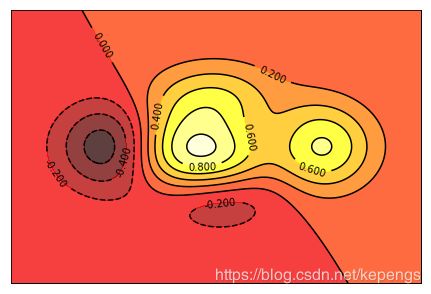
等高线图

In [15]:

def f(x,y):
    return (1-x/2+x**5+y**3)*np.exp(-x**2-y**2)

n = 256
x = np.linspace(-3,3,n)
y = np.linspace(-3,3,n)
X,Y = np.meshgrid(x,y)

plt.axes([0.025,0.025,0.95,0.95])

plt.contourf(X, Y, f(X,Y), 8, alpha=.75, cmap=plt.cm.hot)
C = plt.contour(X, Y, f(X,Y), 8, colors='black', linewidth=.5)
plt.clabel(C, inline=1, fontsize=10)

plt.xticks([]), plt.yticks([])
# savefig('../figures/contour_ex.png',dpi=48)
plt.show()

/Users/sunkepeng/anaconda2/lib/python2.7/site-packages/matplotlib/contour.py:1004: UserWarning: The following kwargs were not used by contour: 'linewidth'
  s)

灰度图（Imshow）

In [16]:

def f(x,y):
    return (1-x/2+x**5+y**3)*np.exp(-x**2-y**2)

n = 10
x = np.linspace(-3,3,3.5*n)
y = np.linspace(-3,3,3.0*n)
X,Y = np.meshgrid(x,y)
Z = f(X,Y)

plt.axes([0.025,0.025,0.95,0.95])
plt.imshow(Z,interpolation='nearest', cmap='bone', origin='lower')
plt.colorbar(shrink=.92)

plt.xticks([]), plt.yticks([])
# savefig('../figures/imshow_ex.png', dpi=48)
plt.show()

/Users/sunkepeng/anaconda2/lib/python2.7/site-packages/ipykernel_launcher.py:5: DeprecationWarning: object of type  cannot be safely interpreted as an integer.
  """
/Users/sunkepeng/anaconda2/lib/python2.7/site-packages/ipykernel_launcher.py:6: DeprecationWarning: object of type  cannot be safely interpreted as an integer.
  

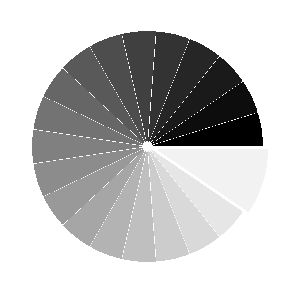
饼状图

In [17]:

n = 20
Z = np.ones(n)
Z[-1] *= 2

plt.axes([0.025,0.025,0.95,0.95])

plt.pie(Z, explode=Z*.05, colors = ['%f' % (i/float(n)) for i in range(n)])
plt.gca().set_aspect('equal')
plt.xticks([]), plt.yticks([])

# savefig('../figures/pie_ex.png',dpi=48)
plt.show()

量场图（Quiver Plots）

In [18]:

n = 8
X,Y = np.mgrid[0:n,0:n]
T = np.arctan2(Y-n/2.0, X-n/2.0)
R = 10+np.sqrt((Y-n/2.0)**2+(X-n/2.0)**2)
U,V = R*np.cos(T), R*np.sin(T)

plt.axes([0.025,0.025,0.95,0.95])
plt.quiver(X,Y,U,V,R, alpha=.5)
plt.quiver(X,Y,U,V, edgecolor='k', facecolor='None', linewidth=.5)

plt.xlim(-1,n), plt.xticks([])
plt.ylim(-1,n), plt.yticks([])

# savefig('../figures/quiver_ex.png',dpi=48)
plt.show()

网格

In [19]:

ax = plt.axes([0.025,0.025,0.95,0.95])

ax.set_xlim(0,4)
ax.set_ylim(0,3)
ax.xaxis.set_major_locator(plt.MultipleLocator(1.0))
ax.xaxis.set_minor_locator(plt.MultipleLocator(0.1))
ax.yaxis.set_major_locator(plt.MultipleLocator(1.0))
ax.yaxis.set_minor_locator(plt.MultipleLocator(0.1))
ax.grid(which='major', axis='x', linewidth=0.75, linestyle='-', color='0.75')
ax.grid(which='minor', axis='x', linewidth=0.25, linestyle='-', color='0.75')
ax.grid(which='major', axis='y', linewidth=0.75, linestyle='-', color='0.75')
ax.grid(which='minor', axis='y', linewidth=0.25, linestyle='-', color='0.75')
ax.set_xticklabels([])
ax.set_yticklabels([])

# savefig('../figures/grid_ex.png',dpi=48)
plt.show()

多重网格

In [20]:

fig = plt.figure()
fig.subplots_adjust(bottom=0.025, left=0.025, top = 0.975, right=0.975)

plt.subplot(2,1,1)
plt.xticks([]), plt.yticks([])

plt.subplot(2,3,4)
plt.xticks([]), plt.yticks([])

plt.subplot(2,3,5)
plt.xticks([]), plt.yticks([])

plt.subplot(2,3,6)
plt.xticks([]), plt.yticks([])

# plt.savefig('../figures/multiplot_ex.png',dpi=48)
plt.show()

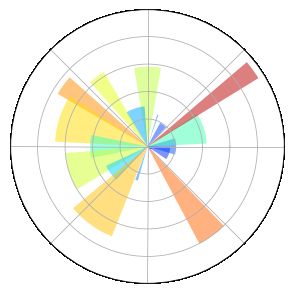
极轴图

In [21]:

ax = plt.axes([0.025,0.025,0.95,0.95], polar=True)

N = 20
theta = np.arange(0.0, 2*np.pi, 2*np.pi/N)
radii = 10*np.random.rand(N)
width = np.pi/4*np.random.rand(N)
bars = plt.bar(theta, radii, width=width, bottom=0.0)

for r,bar in zip(radii, bars):
    bar.set_facecolor( plt.cm.jet(r/10.))
    bar.set_alpha(0.5)

ax.set_xticklabels([])
ax.set_yticklabels([])
# savefig('../figures/polar_ex.png',dpi=48)
plt.show()

3D 图

In [22]:

from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
ax = Axes3D(fig)
X = np.arange(-4, 4, 0.25)
Y = np.arange(-4, 4, 0.25)
X, Y = np.meshgrid(X, Y)
R = np.sqrt(X**2 + Y**2)
Z = np.sin(R)

ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=plt.cm.hot)
ax.contourf(X, Y, Z, zdir='z', offset=-2, cmap=plt.cm.hot)
ax.set_zlim(-2,2)

# savefig('../figures/plot3d_ex.png',dpi=48)
plt.show()

手稿

In [23]:

eqs = []
eqs.append((r"$W^{3\beta}_{\delta_1 \rho_1 \sigma_2} = U^{3\beta}_{\delta_1 \rho_1} + \frac{1}{8 \pi 2} \int^{\alpha_2}_{\alpha_2} d \alpha^\prime_2 \left[\frac{ U^{2\beta}_{\delta_1 \rho_1} - \alpha^\prime_2U^{1\beta}_{\rho_1 \sigma_2} }{U^{0\beta}_{\rho_1 \sigma_2}}\right]$"))
eqs.append((r"$\frac{d\rho}{d t} + \rho \vec{v}\cdot\nabla\vec{v} = -\nabla p + \mu\nabla^2 \vec{v} + \rho \vec{g}$"))
eqs.append((r"$\int_{-\infty}^\infty e^{-x^2}dx=\sqrt{\pi}$"))
eqs.append((r"$E = mc^2 = \sqrt{{m_0}^2c^4 + p^2c^2}$"))
eqs.append((r"$F_G = G\frac{m_1m_2}{r^2}$"))


plt.axes([0.025,0.025,0.95,0.95])

for i in range(24):
    index = np.random.randint(0,len(eqs))
    eq = eqs[index]
    size = np.random.uniform(12,32)
    x,y = np.random.uniform(0,1,2)
    alpha = np.random.uniform(0.25,.75)
    plt.text(x, y, eq, ha='center', va='center', color="#11557c", alpha=alpha,
             transform=plt.gca().transAxes, fontsize=size, clip_on=True)

plt.xticks([]), plt.yticks([])
# savefig('../figures/text_ex.png',dpi=48)
plt.show()

官方画廊

官方网站上有一个丰富的画廊，其中的例子都有配图和对应的代码，当你不知道某一个效果如何实现的时候，你可以在这里找找。

阅读文档

官方文档写的非常好，比如我们主要关注的pyplot文档。

另外，在上面的一些例子中，我们修改了一些线型、颜色之类的属性，它们几乎都是所谓的'magic string'，它们实际上主要来自于MATLAB的定义，你可以在这里找到它们对应的含义。