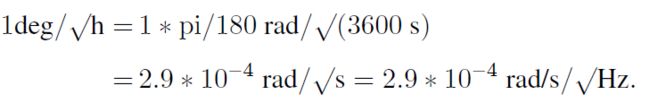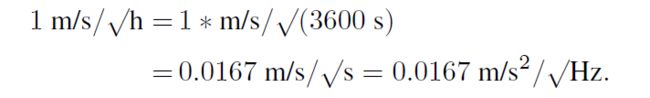陀螺 Allan 方差分析

在IMU选型时，需要重点关注陀螺的随机游走和零偏稳定性参数，这些是影响姿态精度的主要参数。

一般，芯片手册上给定的参数比较理想。需要在拿到硬件后，进行误差分析，多次测试看其性能。

陀螺噪声分析不适用ARMA模型，一般使用阿伦方差分析法对陀螺随机误差分析和建模。

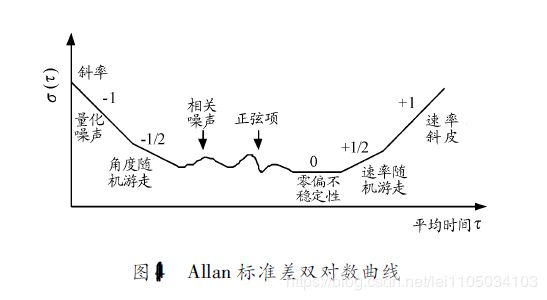
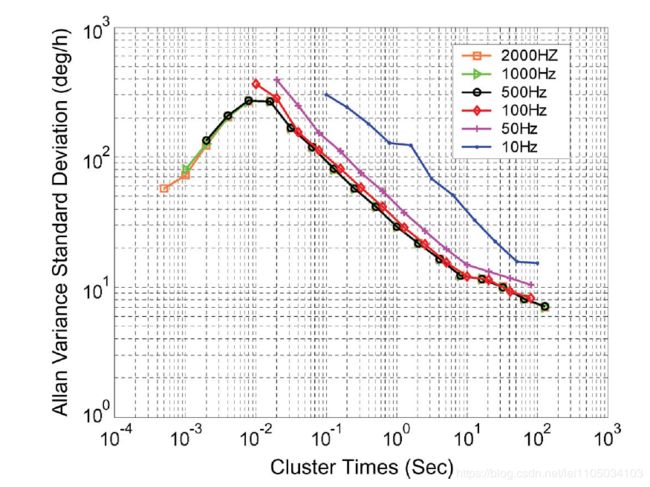
Allan方差法是一种时域分析技术，对实际静态条件下采集的惯性器件数据进行分析得到双对数曲线图，如图1, 根据不同拟合直线的斜率可以辨识不同的误差系数。

Allan方差计算方法

Step1:

假设 IMU的采样周期是Ts，静态采集 N 个点。

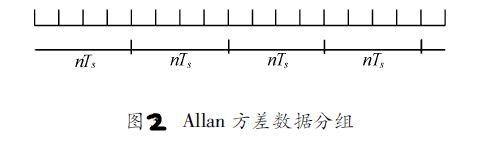
将采样数据划分为包含不同数量采样点的子集 : τ（ｎ）= nTs，n=1,2…N/2 , ，τ（ｎ）为该子集的平均时间

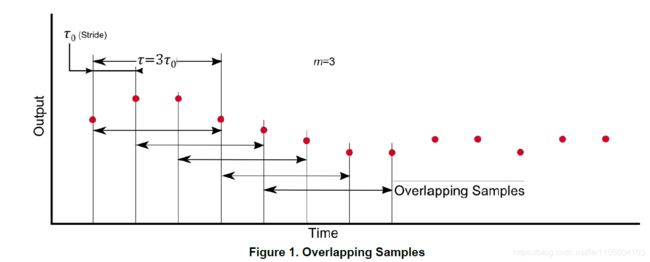
实际中，交叠式阿伦方差常用，下图是 n=3 时的分组情况。

Step2:

对于每一子集，计算第k组和第k+1组内各点的均值序列，再求取相邻两组的差值序列。最终求取所有差值的方差。

这样，就会得到n个在每一平均时间τ（ｎ）对应的方差σ（n）。根据这n个点作图，可得到Allan标准差σ随平均时间τ变化的双对数曲线。

Allan方差反映了相邻两个采样段内平均频率差的起伏。它的最大优点在于对各类噪声的幂律谱项都是收敛的。

Allan方差分析误差与采样总数量和子集内采样点数量有关，总采样时间越长，数据量越大，Allan方差分析结果越准确；子集内数据量少时，平均时间短，Allan方差分析结果准确，而平均时间长时，分析结果差。

 

Step3:

通过曲线拟合 可以得到不同斜率下的误差项。主要有以下5大误差。

1.  量化噪声

量化噪声由AD转换过程中产生，是随机的，互不相关，是白噪声序列。

Allan标准差为 ：

在阿伦标准差相对T的双对数曲线上，斜率为-1， T=√3 处可以读出。

量化噪声的相关时间短，等效频带宽，而运载体的运动频率较低，因此量化噪声容易被低通滤波器过滤，不会成为惯性传感器的主要误差源。

2. 角度随机游走（ARW）

陀螺输出的角速率（加表的线加速度）白噪声，时间积分后为角度（线速度）随机游走。

Allan标准差为 ：

在阿伦标准差相对T的双对数曲线上，斜率为-1/2， T=1 处可以读出。

3. 零偏稳定性

零偏稳定性是指低频零偏抖动，由于内部电路随机波动引起。 代表零偏随时间变化的情况。

Allan标准差为 ：

在阿伦标准差相对T的双对数曲线上，底部的平坦区读出常值。芯片上一般取最小值， 但是常用的是 10s,或者100s处的值，即为平时所说的10s/100s平零偏稳定性。

 

4. 角速率随机游走

相关时间较长的一种噪声，是一种起源不确定的随机过程。

Allan标准差为 ：

在阿伦标准差相对T的双对数曲线上，斜率为+1/2， T=3 处可以读出。

5. 速率斜坡

漂移角速率斜坡是一种确定性系统误差，而不是随机项。

Allan标准差为：

在阿伦标准差相对T的双对数曲线上，斜率为+1， T=√2处可以读出。

 

假设各种误差源统计独立，那总的艾伦方差为各种误差源之和，即

通过曲线拟合后，可以解得各项系数，然后可计算以上误差参数。

噪声类型	计算公式	陀螺单位	加表单位
量化噪声		or  arcsec(角秒)
角度随机游走		or	or    or
零偏稳定性
角速率随机游走
速率斜坡

如果计算时 τ（ｎ）平均时间是 s，陀螺输出是 °/h，A系数是相对 s 的，要转换成相对 h 的，需要按照T的幂次转换。 例如 速率斜坡 R * 3600，K*60等。如果陀螺输出是°/s，A系数需要先转换成°/h，再按上述转换。

当采样频率不一样时，阿伦方差不同。例如，采样频率越低，高频噪声会被抑制。低通滤波器的原理一致，截止频率越低，能抑制短周期噪声，如量化噪声等。但是采样频率一般需要大于IMU 3dB带宽频率的3~5倍。

 

阿伦方差中重要的的两个误差项是角度随机游走（用于设置Q阵）和 零偏稳定性（用于设置KF中一阶马氏过程的方差）。

芯片上一般给出的是常温下的阿伦方差参数，而实际应用中，最好做全温下的阿伦方差分析，因为载体环境温度会变。例如 某款芯片常温下零偏稳定性为3°/h，全温下为 30°/h 。

 

参考严恭敏老师关于阿伦方差的理解~链接:    http://blog.sina.com.cn/s/blog_40edfdc90102y1ar.html

参考网友的matlab程序~链接： https://blog.csdn.net/u012325601/article/details/60882949