机器学习基础
少年听雨歌楼上。红烛昏罗帐。壮年听雨客舟中。江阔云低、断雁叫西风。
而今听雨僧庐下。鬓已星星也。悲欢离合总无情。一任阶前、点滴到天明。
——虞美人·听雨 蒋捷
缘起
机器学习是当前最为热门的话题之一。自动驾驶、神经网络、人工智能等一个个”高大上“ 的词语不禁让我们眼花缭乱。抽丝拔茧后不难发现,这些技术都是与机器学习相关的。实际上,机器学习并不像我们相像中的那么高深,离我们也没有那么遥远,其基本原理还是非常容易理解的。那么,本篇文章就结合周志华老师的西瓜书及李航老师的统计学习方法两本书,对机器学习的相关概念及基本原理进行介绍,让机器学习不再那么遥不可及。
有人告诉我说我,书里每出现一个公式,都会让销量减半。 ——霍金
机器学习和数学及公式的关系极为密切,不涉及公式似乎不可能,但由于本篇只涉及机器学习的基本原理。为了不使读者减半,我决定不引入数学公式。
题外话
人类世界的运行,绝大多数都是由经验所支配的。比如人们认为明天的太阳一定从东方升起,从楼顶扔一块石头一定会向下掉落。同样,所有的物理定律都是对经验的总结,无论是牛顿定律还是量子力学,都是从过去的情形中总结的经验,并且这些经验能很好的预测未来。世界貌似是永远按照物理定律的规定在认真的运行着。
但是:
从来如此,便对么? ——鲁迅
之前有一千年甚至一亿年太阳都从东方升起,那明天的太阳就一定从东方升起吗?之前太阳的升起规律,就一定适用于明天吗? 当太阳一次次的从东方升起后,只能是增加了明天太阳从东方升起的可能性,并不能保证明天一定是这样。根据过去情形总结的经验,并一定能适用于未来。
我们生活在经验中,我们根据经验预测未来。但未来像一个调皮的孩子,它并不一定听我们的,虽然它已经听了很多次。也就是说,未来与过去,并没有必然的因果关系,即使我们从过去总结规律已经被验证了无数次。有因必有果,不一定是对的。
机器学习是什么
虽然从历史中总结的规规律不能决定未来,但是,如果一个规律在历史上被一次又一次的验证,我们就可以用此规律来预测未来,虽然这种预测可能不是100% 准确。
机器学习和上面所说的经验有什么关系呢?实际上,机器学习和我们人类活动非常类似,它的作用就是从大量的数据中学习到经验。并且将此经验运用到对未来数据的处理和分析中。《统计学习方法》一书中对机器学习做了如下的定义:
统计学习是关于计算机基于数据构建概率统计模型并运用模型对数据进行预测与分析的一门学科,统计学习也称为统计机器学习
我觉得这一定义是非常准确的。从中,我们可以总结出如下内容:
- 机器学习的主体:计算机,这也是机器学习这一名称的由来。
- 机器学习的作用对象:数据,也即历史数据。
- 机器学习的产出:概率统计模型,通常简称为模型。
- 机器学习的目标:运用产出的模型对数据进行预测和分析。即对未来的数据进行预测和分析,注意这里包含了预测和分析两项活动。
上述定义还隐含了一个内容,在利用数据构建模型的过程中,计算机实际上是利用了学习算法来生成模型的。
从上述分析中不难看出,机器学习的过程,和人类利用经验来预测未来的行为非常相似。都是利用历史经验来预测未来。那么,这里的 “历史经验” 就是从数据中得到的模型。因而,我们可以总结出如下的关系:
模型就是总结出来的规律或经验,利用某个算法从数据中产生模型的过程就称为“学习”,模型所代表的规律或经验,就称为知识。这些定义都是为了贴近人类的真实活动且便于理解而进行的命名。这里的算法和常见的算法不太一样,都是机器学习领域专用的算法。
这里举一个可以使用机器学习的例子。例如要判断一个西瓜是好瓜还是坏瓜,我们已经有了如下的历史的数据(假设西瓜好坏完全是由色泽、根蒂、敲声三个特点完全决定):

当我们遇到一个新的西瓜时,如果它是青绿、蜷缩、浊响的,我们根据上表就可以知道这是一个好瓜,这就是利用了历史的经验对新数据进行了分析预测,这就是机器学习的过程。
上表中色泽、根蒂、敲声这些特点,在机器学习中,被称为特征(attribute/feature) ,而是否是好瓜这些结果,被称为标记(label)。表中的每行示例,都实际上都表示了多个输入到一个输出的映射关系,即多个特征到一个标记之间的映射关系。表中的每一行,在数学上都可以表示为一个行向量 X(有三个子元素) 到标量y 的对应关系。
编程中,我们通常会定义函数,函数的作用是给定输入,产生输出。那么机器学习(监督学习,见下方)的过程与此恰好相对,是给定输入和输出,让我们来估计函数映射关系。可以看出,机器学习的过程就是一个进行”拟合“的过程,拟合的定义如下:
科学和工程问题可以通过诸如采样、实验等方法获得若干离散的数据,根据这些数据,我们往往希望得到一个连续的函数(也就是曲线)或者更加密集的离散方程与已知数据相吻合,这过程就叫做拟合(fitting)。
机器学习的分类
根据原始数据的形式可以将机器学习分为监督学习、非监督学习、半监督学习和强化学习。本文只涉及监督和非监督学习。
监督学习
如果原始数据中既含有数据,又含有标记,那么这种学习叫做监督学习。监督学习生成的模型用于预测新输入的结果,例如根据表1.1 中的数据预测遇到的新瓜是好是坏。
在监督学习中,如果数据的标记是离散值,我们称这种机器学习问题为分类问题,特别的,如果类别只有两种,就像西瓜只有好、坏两种,我们称为二分类问题。如果原始数据中的标记以及要预测的标记并不是表1.1中好、坏这种离散值,而是连续的值,例如 0.5,0.81 等等,我们称为回归问题。
无监督学习
当然,我们遇到的问题并不全是有标记的理想数据,也有可能是没有标记、只有特征的数据。那么,这类数据中会有什么规律呢?和我们常说的“物以类聚,人以群分“一样,我们遇到的数据即使没有标记,其分布也很可能是有一定规律的。那么,对无标记的数据进行学习的过程,就称为无监督学习。在无监督学习中,有一种学习产生的结果和”人以群分“ 的效果一样,称为”聚类“。例如如我们有一组无标记的数据,有两个特征,其特征分布特性如下图所示:
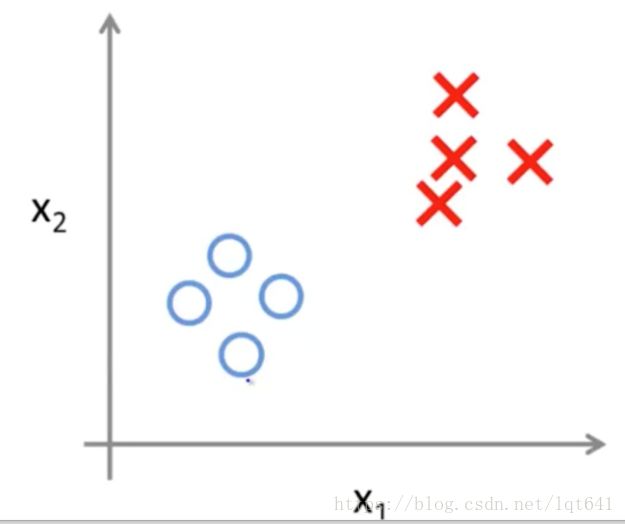
可以看出,数据很明显的分为了两个部分。对于无标记的数据,无监督学习就是要找到类似于上图一样的分布规律。
机器学习的一些概念
数据集
我们用于机器学习整个过程的含有特征和标记的原始数据,被称为数据集。数据集也被称为样本集,每行数据称为一个样本。数据集通常被划分为三个部分:训练集、验证集、测试集,这三个集合通常是没有交集的。
训练集
对模型进行训练的数据集被称为训练集。在不同的上下文中,训练集的含义是不一样的。在训练模型时,训练集是整个数据集。在模型评估时,用于训练评估模型的数据集的子集,也训练集。无论是何种情形下,用于对模型或评估模型进行训练的集合就是训练集。
验证集
一个模型中通常有许多参数,为了确定这些参数的较优值,我们需要从原始数据集中独立划分出一部分数据。这个数据子集被称为验证集。
测试集
机器学习的算法有很多,针对同一数据集,两个不同的算法训练出来不完全同的模型,那么如何对比这两个模型的好坏呢?模型好坏是通过对未知数据的预测准确率来衡量的。为了测试模型对未知数据的预测准确性,我们在进行模型评估时,从数据集中额外再划分出一部分,做为测试集。在使用时,认为测试集属于未知的数据。把测试集的特征输入模型后,将产生的结果与测试集的标记进行对比,就可以得到模型在未知数据上的近似效果。模型在未知数据上的效果,被称为模型的泛化能力。对未知数据的预测越准确,模型的泛化能力越好。
假设空间
在机器学习中,“假设”是指从输入到输出的映射关系,即函数。假设空间就是输入到输出映射函数的集合,需要注意的是,假设空间中既包含正确的假设,也可以包含错误的假设。我们进行机器学习的目的,就是从假设空间中找到和已有数据相匹配的这些假设,即筛选出正确的假设。从集合论的角度来看,如果一个集合是某个问题的假设空间,那么包含这个集合的所有父集合,必定也是假设空间。例如,一个集合包含了任意输入到输出的所有映射函数,那么这个集合一定是假设空间,因为这个集合中一定包含了任意给定数据所蕴含的函数映射关系。
在实际应用中,我们通常可以排除一些显然不符合当前映射关系的假设,从而可以缩小当前假设空间的大小,使问题便于处理。
版本空间
与已知数据集一致的所有假设的集合,可以为版本空间是恰好包含了所有正确假设的集合。
样本空间
样本空间同样是一个集合,是指含有所有可能的特征的数据集合,在计算样本空间大小时,不考虑数据的标记。因而样本空间的大小就是所有可能的特征值的组合。在表1.1中,假设色泽、根蒂、敲声分别有两种、三种、三种,那么样本空间的大小就是 2x3x3= 18 种。
假设和样本的区别
在知乎上有人问到假设空间和样本空间的区别。在西瓜书中,假设空间中包含如下的内容:
色泽=青绿;根蒂=蜷缩;敲声=浊响而样本空间中也包含了这样的一组数据,难道有问题吗?实际上是没有问题的,只是这样一组信息在不同的上下文中解读的方式不一样。
上文已经述及,假设是指映射关系,那么当上述信息位于假设空间中时,它就表示了满足这样信息的瓜是好瓜,它的作用和一个映射函数是一样的。
而当这条信息位于样本空间中时,它代表的是数据,与标记一起标识了一条静态的信息,这一数据做为机器学习作用的对象。
除此之外,假设空间和样本空间另外的区别就:假设空间会包含含有通配符的假设(映射关系):
色泽=青绿;根蒂=蜷缩;敲声=*它表示当一个瓜是青绿、根蒂蜷缩、敲声无论怎样,都是一个好瓜,它表示的依然是映射关系。
而样本空间中的数据一定是不含有通配符的,它表示真实存在的一个静态的数据实例。
机器学习的”坑”
坑之——经验误差与泛化误差
当用原始数据集训练出一个模型后,我们需要验证这个模型的好坏。把数据集中的样本再次输入到模型后,产生的输出和数据集已有的标记数据可能不一致,这种误差就叫做训练误差,或经验误差。在某些情况下,经验误差可以做到很小,甚至为0,表示当前的模型能完全的匹配当前的数据集。
但是,与训练集完全匹配,并不能代表模型在新样本上的效果。我们期望的是:模型在新的样本上能有较好的表现。新样本在模型上的输出,与新样本真实的标记之间的误差,称为泛化误差。通常,新样本的标记我们是不知道的,也即泛化误差是未知的。即使我们把原始数据分为了训练集、验证集、测试集,在测试集上的误差,也仅仅是代表了模型在一小部分新样本上的效果,代表不了整体的未知数据的泛化误差。由于我们获取到的数据的有限性,只能用测试集上的误差来代表泛化误差。
由于只能用测试误差来代替泛化误差,在进行模型评估时就必然存在一定的偏差。
坑之——过拟合与欠拟合
如果训练得到的模型,能够精确匹配给定的数据集,那这个模型是不是就非常好了呢? 不是的。实际上我们更关注的是模型在新样本上的表现。对新样本有很好预测能力的模型才是我们需要的。为了达到这个目的,我们希望能从已知数据中学得所有潜在样本拥有的“普遍规律”。
然而,如果一个模型对训练样本匹配程度太好的时候,这个模型很可能把已知样本的一些特有的特性当成了所有样本的普遍特性,这就会导致模型的泛化能力下降,并不能很好的用于新样本的预测,这种现象在机器学习中称为“过拟合”,即学习的“过度”了。与“过拟合”相对应的是“欠拟合”,是指习得的模型不能很好的匹配已知数据集。下图很好的表现了过拟合和欠拟合的情况:
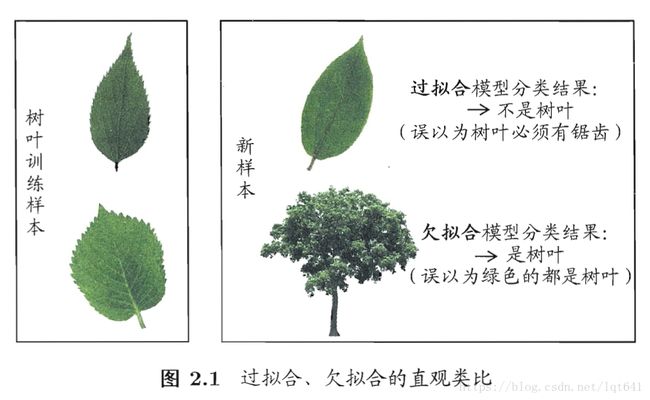
坑之——归纳偏好
对于给定的数据集,很可能有多个假设都能很好的匹配这些数据,仍然以表1.1 中数据为例:

下表中的三个假设都能很好的匹配的表1.1中的数据:
- 色泽=* 根蒂=蜷缩 敲声=*
- 色泽=* 根蒂=* 敲声=浊响
- 色泽=* 根蒂=蜷缩 敲声=浊响
当假设有一个新的瓜,它的特点是:色泽=青绿 根蒂=蜷缩 敲声=沉闷,对于这个新瓜,如果应用第一个假设,那么它就是一个好瓜,如果用第二个或第三个假设,那么这就是一个坏瓜。显然,对于新瓜好坏的判断,我们要用 一个统一的假设,不能一会判定为好瓜,一会又判定为坏瓜,也就是在多个都正确的假设中,我们不得不只选择一个假设作为最终的结果。在机器学习中,这种对某类型假设的偏好,称为“归纳偏好”。任何一个机器学习算法,必须有其归纳偏好,否则就会出现类似于上面的”时好时坏“的判定结果。
归纳偏好的作用在图1.3这个回归学习中表现的更为直观。对于已有样本数据(图中的离散点),假设我们找到了两个假设,即A和B 两个函数。可以看出,这两个假设都能很好的匹配给定的点。
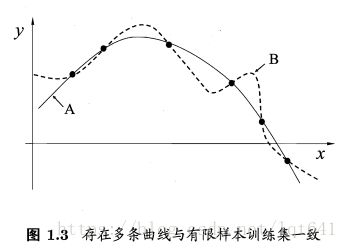
无论是西瓜问题中的多个匹配的假设,还是图1.3中A、B两条曲线,在多个等效假设中,我们无法判定哪一个假设是优于其他的,即无法做出偏好选择。这就导致我们必须引入其他的原则,来处理这类多假设匹配问题。
在进行偏好选择时,经常使用的一个原则,就是“奥卡姆剃刀”原则,即“若有多个假设与与观察一致,选择最简单的那个”。在图1.3中,假设曲线更平滑表示更简单,那么,曲线A将成为我们的偏好选择。
但是,在多个等效假设时,使用“奥卡姆剃刀原则”依然有问题,那就是其中的“更简单”如何定义。例如在西瓜问题中,下述两个与数据匹配的假设,哪个更简单呢?
色泽=* 根蒂=蜷缩 敲声=*
色泽=* 根蒂=* 敲声=浊响对于图1.3中的问题,假设黑点代表训练样本,白点表示测试集:
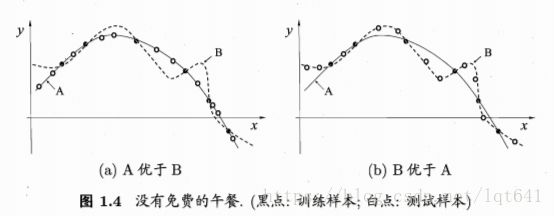
在 1.4(a) 的情形中,曲线 A 与测试集的匹配程序更好,即在此时,A 的泛化能力更好。但在 1.4(b) 的情形下,B的泛化能力更好。这时奥卡姆剃刀原则不再适用。可以看出,对于两个假设,在某些问题上,A 可能优于B,而在另外的问题上,B 可能优于 A,这是对任何机器学习算法都存在的问题。
在数学上可以证明,一个经过机器学习得到的模型,与随机选择结果的模型,其在训练集外的误差期望是相同的。即经过机器学习的模型在泛化能力上,并不比随机分类好。这一情况出现的原因是:我们想要用有限的样本,去预测无限的新样本。
吾生也有涯,而知也无涯。以有涯随无涯,殆已! ——庄子
但是,机器学习模型与随机选择的误差期望相同是有前提的,就是认为:已知样本集相对于未知的样本,数量及其内在的规律是可以忽略的。而我们在真正进行机器学习时,如果数据集足够大,那么数据集通常是能在很大程度上反映整体的规律的。比如对于样本中两个都正确的假设,如果其中一个假设对应的已知样本数量远大于另一个,那么我们就可以选择样本数量大的假设。
坑之——模型评估
这里所说的模型评估是指:使用数据D 和某种算法训练出一个模型,然后对此模型的泛化能力进行评估,即对泛化误差进行评估。
上面已经述及,泛化误差只能用测试误差来近似的估计。为了使测试误差尽可能的接近泛化误差,在划分训练集、验证集、测试集时就要遵守一定的原则。划分各集合时最基本的要求就是:各集合间是互斥的,即集合间不能有交集。因为一旦有了交集,相交的这一部分数据就相当于用已经学习过的数据来测试模型,结果是不可信的。在集合划分互斥的基础上,为了保证集合划分的合理性及模型选择的可靠性,我们可以用如下几类方法进行集合的划分,对模型中算法进行评估。在下面论述时,训练集实际上同时包含了训练集和验证集,因而数据集D 中只包含训练集 S 和测试集 T。
留出法
留出法是指直接将数据集划分为两个互斥的集合,一个作为训练集 S,一个作为测试集 T。在S 上训练出供评估用的模型后,用 T 的误差即测试误差,作为对泛化误差的估计,注意,这里在 S 上训练的模型只用于误差计算,计算的误差用于评估的是用数据集D训练出来的模型。
划分 S 和 T 时,要尽量保持 S、T 中的数据分布与之前的数据集 D 中数据分布的一致性,避免在划分过程中引入额外的偏差。例如在西瓜问题中,假设数据集中共有1000个瓜,其中好瓜800个,坏瓜200个,即好瓜为80%,坏瓜占20%,为保证数据分布不变,在划分成 S 和 T 后,S 和 T 中的好瓜比例也应该占80%。例如在划分数据集时,假设我们按 3:2 的比例划分训练集和测试集,即 S 含有600个瓜,T 中有400个瓜,按 80% 的好瓜比例,S中应该含有 600*80%=480 个好瓜,而T 中应该含有400x80% = 320 个好瓜。在训练集和测试集中保持这种分布的稳定定,能保证模型输出结果和数据集D 的一致性。
需要注意的是S 和 T 集合的大小问题。如果训练集过大,就会导致测试集过小,无法充分验证模型的泛化能力;如果训练集过小,就会导致生成的模型与原始数据集 D 的偏差过大,导致欠拟合。这个问题没有完美的解决方案,通常是选择 数据集中 2/3 ~ 4/5 的数据作为训练集。
由于对数据集进行不同的划分会产生不同的模型,单次留出法产生的模型通常不够可靠,因而在使用时,通常对数据集进行多次划分,得到多个测试误差,将所有测试误差取平均值做为模型的最终泛化误差。
交叉验证法
交叉验证法是指把数据集 D 均分成 k 个大小相同的互斥子集,子集中同样要保持和数据集D 相同的数据分布。使用时,用 k-1 个子集的并集作为训练集,剩下的1个子集作为测试集,这样就可以获得 k 组训练集/测试集,训练出k个评估模型后,计算出k个测试误差,最终同样取k个测试误差的均值作为模型(用 D 训练出的)的泛化误差。
可以看出,交叉验证结果的准确性和稳定性与 k 的选择有很大的关系,为了强调这一点,通常将交叉验证法称为k拆交叉验证法 (k-fold cross validation)。在际应用中,k通常取10,即 10 折交叉验证,基示意图如下:
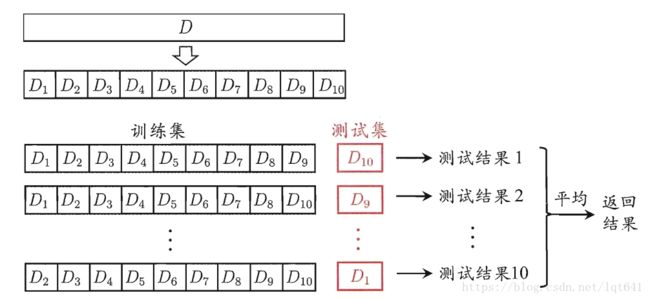
在 k 值确定的情况下,将同一个数据集D 划分为 k 个子集集的方式也是多种多样的。为了保证结果的可靠性,可以将集合进行多次随机划分,每次划分都使用 k 折交叉验证,即 p 次 k 折交叉验证,最终的评估结果使用 p 次结果的均值,通常使用的是 10 次 10 折交叉验证。
假设 数据集D 中有m 个样本,在使用 k 折交叉验证时,我们得到了一类特殊的情况:划分的每个子集中只有一个样本,这种方法称为留一法。由于这时的训练集与数据集D 只差一个样本,留一法训练出的模型与 D 训练出的模型相似度会非常高,这样得到的误差评估结果会比较准确。但是,如果数据集中的样本数量过大,使用用 p 次 k 折交叉验证时,计算量会非常大,如果再考虑到模型调参,计算量会更大,甚至变得不可行,这时留一法就不再适用了。
自助法
留出法和 k 折交叉验证法在计算测试误差时,使用的模型都是用数据集 D 的子集训练出来的,相比于用数据集D全集训练出来的模型,子集训练时由于训练样本的规模不同而会导致误差产生。留一法的训练集规模和全集D较为类似,但由于计算量较大,也有一定的问题。
为了保证评估测试误差时训练集和全集的规模较为类似,在模型评估时引入了自助法。自助法的具体操作为:对于具有m 个样本的数据集,通过采样产生新的数据集,每次从 m 个样本中随机抽取一个样本放入新的数据集,之后再将此样本放回原数据集 D,保证D的规模不变。将上述过程重复 m 次后,我们就得到了一个和原始数据集大小一样的集合 D′ D ′ ,这种方法称为自助采样法。在数学上可以证明,通过自助采样,原始数据集D中约为 36.8% 的样本未出现在新的集合 D′ D ′ 中,这同时也表明了 D′ D ′ 中有重复的样本。
进行测试误差评估时,用 D′ D ′ 进行模型训练,用 D−D′ D − D ′ (差集)作为测试集。由于 D−D′ D − D ′ 与 D′ D ′ 并无
交集,因而这一差集能对模型进行较好的评估。
自助法在数据集较小、难以有效划分训练集和测试集时较为有用。但是要注意的是,自助采样法改变了最初数据集的分布,这会在误差评估时引入新的偏差。因而在数据集足够时,留出法和交叉验证法更常用一些。
坑之——算法选择
是不是我对各个算法足够了解,算法和数学原理非常熟悉甚至能手动推导,就表示在实际中我能很好的应用机器学习了呢?不是的。
在实际应用中,比如广告点击率预估、文本分类、垃圾邮件识别、图像识别等,大部分都是分类问题。那么,针对分类问题的多个算法,我们应该选择哪个呢?在书上介绍垃圾邮件分类时,通常会用朴素贝叶斯算法,那么为什么用这个算法而不是别的算法呢?有人说是经验,经过对比这个算法的效果更好,那么在现实中的各种邮箱例如 Gmail 或QQ邮箱中的垃圾过滤,一定用的是贝叶斯吗?另外就是遇到一个全新的分类问题,在没有经验的情况下,我们该如何在众多的算法中进行选择?把所有算法都两两对比过来显然是不现实的。
因而即使学习完各种高大上的模型和公式之后,选择正确的算法,依然是一个很困难的现实问题,这就需要对当前问题有深入的了解,并且有丰富的算法使用经验。
坑之——调参
假设你非常牛,深入了解各种算法及机器学习理论,针对某个问题选择了正确的算法,之后你会发现——大多数学习算法都有些参数需要设定。参数设置不同,训练得到的模型就会不同,性能也会有较大差别。因而在进行机器学习时,除了选择适当的算法,还需要对算法的参数进行设定,这就是通常所说的参数调节,即调参。
令人十分崩溃的是,一个机器学习算法中需要调节的参数往往不只是一个,更悲剧的,好多参数都是连续值,可以在一个实数范围内任意取值。简而言之,一个算法中的参数组合可能有无数种。通常进行了一个折中就是把连续值进行区间段采样,这样能减少一部分工作量,但很显然,抽样会使调参结果“打折扣”。
坑之——数据
假设有了机器学习算法,有了合适的参数,但要得到一个有高度泛化能力的模型,还需要有良好的数据输入。如果数据本身就有问题,再好的算法也无用。机器学习的过程本质上是模拟了人类的学习过程,即从已有知识中学得经验。如果最初的标记数据有误,那么模型学得的经验就是不可靠的,对未来数据进行可靠的预估更是无从谈起。
要得到可靠的数据就要进行数据清洗,而最可靠的数据清洗方式就是人工标注。因为机器学习最终是要解决人类的问题,对于训练数据,只有人才能对其分类进行准确的判定。但是,人工标注会导致非常高的成本投入,通常较大的公司才有足够的人力和原始数据来进行标注。
结语
机器学习的基本原理还是比较容易理解的。对于大多数程序员来说,学习机器学习是不需要对其中的数学原理有深入理解的。从上文的论述也可以看出,机器学习中的大部分的“坑”并不是出现在数学的艰深和算法的复杂性上。因而,如果你是一名机器学习应用方面的 “算法”工程师,我建议把重点放在实际应用上的 “坑” 上面,而不是算法和数学理论的推导上
。那些“高大上” 的事情,请留给数学家和算法科学家们。毕竟,成为一个实践经验丰富的、合格的机器学习工程师和数据分析工程师,也不是那么容易的,而这些,才是工程中真正需要的。
虽然机器学习中的 “坑” 看似很多,但只要我们了解了这些问题产生的原因,在面对具体问题时进行适当的折中,机器学习通常还是能产生非常不错的效果的。
The End
参考文献
[1] 朱孝臧. 宋词三百首
[2] 周志华. 机器学习. 清华大学出版社.
[3] 李航. 统计学习方法. 清华大学出版社.
[4] https://segmentfault.com/a/1190000007423515
[5] http://www.sharpsightlabs.com/blog/machine-learning-prerequisite-isnt-math/
我就是我,疾驰中的企鹅。
