CHAPTER 2 How the backpropagation algorithm works

In the last chapter we saw how neural networks canlearn their weights and biases using the gradient descent algorithm.There was, however, a gap in our explanation: we didn't discuss how tocompute the gradient of the cost function. That's quite a gap! Inthis chapter I'll explain a fast algorithm for computing suchgradients, an algorithm known as backpropagation.

The backpropagation algorithm was originally introduced in the 1970s,but its importance wasn't fully appreciated until afamous 1986 paper byDavid Rumelhart,Geoffrey Hinton, andRonald Williams. That paper describes severalneural networks where backpropagation works far faster than earlierapproaches to learning, making it possible to use neural nets to solveproblems which had previously been insoluble. Today, thebackpropagation algorithm is the workhorse of learning in neuralnetworks.

This chapter is more mathematically involved than the rest of thebook. If you're not crazy about mathematics you may be tempted toskip the chapter, and to treat backpropagation as a black box whosedetails you're willing to ignore. Why take the time to study thosedetails?

The reason, of course, is understanding. At the heart ofbackpropagation is an expression for the partial derivative ∂C/∂w

of the cost function C with respect to any weight w (or bias b

) in the network. The expression tells us how quicklythe cost changes when we change the weights and biases. And while theexpression is somewhat complex, it also has a beauty to it, with eachelement having a natural, intuitive interpretation. And sobackpropagation isn't just a fast algorithm for learning. It actuallygives us detailed insights into how changing the weights and biaseschanges the overall behaviour of the network. That's well worthstudying in detail.

With that said, if you want to skim the chapter, or jump straight tothe next chapter, that's fine. I've written the rest of the book tobe accessible even if you treat backpropagation as a black box. Thereare, of course, points later in the book where I refer back to resultsfrom this chapter. But at those points you should still be able tounderstand the main conclusions, even if you don't follow all thereasoning.

Warm up: a fast matrix-based approach to computing the output from a neural network

Before discussing backpropagation, let's warm up with a fastmatrix-based algorithm to compute the output from a neural network.We actually already briefly saw this algorithmnear the end of the last chapter, but I described it quickly, so it'sworth revisiting in detail. In particular, this is a good way ofgetting comfortable with the notation used in backpropagation, in afamiliar context.

Let's begin with a notation which lets us refer to weights in thenetwork in an unambiguous way. We'll use wljk

to denote theweight for the connection from the kth neuron in the (l−1)th layer to the jth neuron in the lth

layer. So, for example, the diagram below shows the weight on aconnection from the fourth neuron in the second layer to the secondneuron in the third layer of a network:

This notation is cumbersome at first, and it does take some work tomaster. But with a little effort you'll find the notation becomeseasy and natural. One quirk of the notation is the ordering of the j and k indices. You might think that it makes more sense to use j to refer to the input neuron, and k to the output neuron, notvice versa, as is actually done. I'll explain the reason for thisquirk below.

We use a similar notation for the network's biases and activations.Explicitly, we use blj

for the bias of the jth neuron inthe lth layer. And we use alj for the activation of the jth neuron in the lth

layer. The following diagramshows examples of these notations in use:

With these notations, the activation alj of the jth neuron in the lth layer is related to the activations in the (l−1)th layer by the equation (compareEquation (4) and surroundingdiscussion in the last chapter)

alj=σ(∑kwljkal−1k+blj),(23)

where the sum is over all neurons k in the (l−1)th layer. Torewrite this expression in a matrix form we define a weight matrix wl for each layer, l . The entries of the weight matrix wl are just the weights connecting to the lth layer of neurons,that is, the entry in the jth row and kth column is wljk .Similarly, for each layer l we define a bias vector, bl .You can probably guess how this works - the components of the biasvector are just the values blj , one component for each neuron inthe lth layer. And finally, we define an activation vector al whose components are the activations alj .

The last ingredient we need to rewrite (23) in amatrix form is the idea of vectorizing a function such as σ

.We met vectorization briefly in the last chapter, but to recap, theidea is that we want to apply a function such as σ to everyelement in a vector v . We use the obvious notation σ(v) todenote this kind of elementwise application of a function. That is,the components of σ(v) are just σ(v)j=σ(vj) .As an example, if we have the function f(x)=x2 then thevectorized form of f has the effect

f([23])=[f(2)f(3)]=[49],(24)

that is, the vectorized f

just squares every element of the vector.

With these notations in mind, Equation (23) canbe rewritten in the beautiful and compact vectorized form

al=σ(wlal−1+bl).(25)

This expression gives us a much more global way of thinking about howthe activations in one layer relate to activations in the previouslayer: we just apply the weight matrix to the activations, then addthe bias vector, and finally apply the σ function* *By the way, it's this expression that motivates the quirk in the wljk notation mentioned earlier. If we used j to index the input neuron, and k

to index the output neuron, then we'd need to replace the weight matrix in Equation (25) by the transpose of the weight matrix. That's a small change, but annoying, and we'd lose the easy simplicity of saying (and thinking) "apply the weight matrix to the activations".. That global view is often easier andmore succinct (and involves fewer indices!) than the neuron-by-neuronview we've taken to now. Think of it as a way of escaping index hell,while remaining precise about what's going on. The expression is alsouseful in practice, because most matrix libraries provide fast ways ofimplementing matrix multiplication, vector addition, andvectorization. Indeed, thecodein the last chapter made implicit use of this expression to computethe behaviour of the network.

When using Equation (25) to compute al

,we compute the intermediate quantity zl≡wlal−1+bl along the way. This quantity turns out to be useful enough to beworth naming: we call zl the weighted input to the neuronsin layer l . We'll make considerable use of the weighted input zl later in the chapter. Equation (25) issometimes written in terms of the weighted input, as al=σ(zl) . It's also worth noting that zl has components zlj=∑kwljkal−1k+blj , that is, zlj is just theweighted input to the activation function for neuron j in layer l

.

The two assumptions we need about the cost function

The goal of backpropagation is to compute the partial derivatives ∂C/∂w

and ∂C/∂b of the costfunction C with respect to any weight w or bias b in thenetwork. For backpropagation to work we need to make two mainassumptions about the form of the cost function. Before stating thoseassumptions, though, it's useful to have an example cost function inmind. We'll use the quadratic cost function from last chapter(c.f. Equation (6)). In the notation ofthe last section, the quadratic cost has the form

C=12n∑x∥y(x)−aL(x)∥2,(26)

where: n is the total number of training examples; the sum is overindividual training examples, x ; y=y(x) is the correspondingdesired output; L denotes the number of layers in the network; and aL=aL(x) is the vector of activations output from the networkwhen x

is input.

Okay, so what assumptions do we need to make about our cost function, C

, in order that backpropagation can be applied? The firstassumption we need is that the cost function can be written as anaverage C=1n∑xCx over cost functions Cx forindividual training examples, x . This is the case for the quadraticcost function, where the cost for a single training example is Cx=12∥y−aL∥2

. This assumption will also hold true forall the other cost functions we'll meet in this book.

The reason we need this assumption is because what backpropagationactually lets us do is compute the partial derivatives ∂Cx/∂w

and ∂Cx/∂b for a single trainingexample. We then recover ∂C/∂w and ∂C/∂b by averaging over training examples. In fact, with thisassumption in mind, we'll suppose the training example x has beenfixed, and drop the x subscript, writing the cost Cx as C .We'll eventually put the x

back in, but for now it's a notationalnuisance that is better left implicit.

The second assumption we make about the cost is that it can be writtenas a function of the outputs from the neural network:

For example, the quadratic cost function satisfies this requirement,since the quadratic cost for a single training example x may bewritten as

C=12∥y−aL∥2=12∑j(yj−aLj)2,(27)

and thus is a function of the output activations. Of course, thiscost function also depends on the desired output y , and you maywonder why we're not regarding the cost also as a function of y .Remember, though, that the input training example x is fixed, and sothe output y is also a fixed parameter. In particular, it's notsomething we can modify by changing the weights and biases in any way,i.e., it's not something which the neural network learns. And so itmakes sense to regard C as a function of the output activations aL alone, with y merely a parameter that helps define thatfunction.

The Hadamard product, s⊙t

The backpropagation algorithm is based on common linear algebraicoperations - things like vector addition, multiplying a vector by amatrix, and so on. But one of the operations is a little lesscommonly used. In particular, suppose s

and t are two vectors ofthe same dimension. Then we use s⊙t to denote the elementwise product of the two vectors. Thus the components of s⊙t are just (s⊙t)j=sjtj . As an example,

[12]⊙[34]=[1∗32∗4]=[38].(28)

This kind of elementwise multiplication is sometimes called theHadamard product or Schur product. We'll refer to it asthe Hadamard product. Good matrix libraries usually provide fastimplementations of the Hadamard product, and that comes in handy whenimplementing backpropagation.

The four fundamental equations behind backpropagation

Backpropagation is about understanding how changing the weights andbiases in a network changes the cost function. Ultimately, this meanscomputing the partial derivatives ∂C/∂wljk

and ∂C/∂blj . But to compute those, we firstintroduce an intermediate quantity, δlj , which we call the error in the jth neuron in the lth layer.Backpropagation will give us a procedure to compute the error δlj , and then will relate δlj to ∂C/∂wljk and ∂C/∂blj

.

To understand how the error is defined, imagine there is a demon inour neural network:

The demon sits at the jth neuron in layer l . As the input to theneuron comes in, the demon messes with the neuron's operation. Itadds a little change Δzlj to the neuron's weighted input, sothat instead of outputting σ(zlj) , the neuron instead outputs σ(zlj+Δzlj) . This change propagates through laterlayers in the network, finally causing the overall cost to change byan amount ∂C∂zljΔzlj .

Now, this demon is a good demon, and is trying to help you improve thecost, i.e., they're trying to find a Δzlj

which makes thecost smaller. Suppose ∂C∂zlj has a largevalue (either positive or negative). Then the demon can lower thecost quite a bit by choosing Δzlj to have the opposite signto ∂C∂zlj . By contrast, if ∂C∂zlj is close to zero, then the demoncan't improve the cost much at all by perturbing the weighted input zlj . So far as the demon can tell, the neuron is already prettynear optimal* *This is only the case for small changes Δzlj , of course. We'll assume that the demon is constrained to make such small changes.. And so there's a heuristic sense inwhich ∂C∂zlj

is a measure of the error inthe neuron.

Motivated by this story, we define the error δlj

of neuron j in layer l by

δlj≡∂C∂zlj.(29)

As per our usual conventions, we use δl to denote the vectorof errors associated with layer l . Backpropagation will give us away of computing δl for every layer, and then relating thoseerrors to the quantities of real interest, ∂C/∂wljk and ∂C/∂blj

.

You might wonder why the demon is changing the weighted input zlj

.Surely it'd be more natural to imagine the demon changing the outputactivation alj , with the result that we'd be using ∂C∂alj as our measure of error. In fact, if you dothis things work out quite similarly to the discussion below. But itturns out to make the presentation of backpropagation a little morealgebraically complicated. So we'll stick with δlj=∂C∂zlj as our measure of error* *In classification problems like MNIST the term "error" is sometimes used to mean the classification failure rate. E.g., if the neural net correctly classifies 96.0 percent of the digits, then the error is 4.0 percent. Obviously, this has quite a different meaning from our δ

vectors. In practice, you shouldn't have trouble telling which meaning is intended in any given usage..

Plan of attack: Backpropagation is based around fourfundamental equations. Together, those equations give us a way ofcomputing both the error δl

and the gradient of the costfunction. I state the four equations below. Be warned, though: youshouldn't expect to instantaneously assimilate the equations. Such anexpectation will lead to disappointment. In fact, the backpropagationequations are so rich that understanding them well requiresconsiderable time and patience as you gradually delve deeper into theequations. The good news is that such patience is repaid many timesover. And so the discussion in this section is merely a beginning,helping you on the way to a thorough understanding of the equations.

Here's a preview of the ways we'll delve more deeply into theequations later in the chapter: I'llgive a short proof of the equations, which helps explain why they aretrue; we'll restate the equations in algorithmic form as pseudocode, andsee how thepseudocode can be implemented as real, running Python code; and, inthe final section of the chapter, we'll develop an intuitive picture of whatthe backpropagation equations mean, and how someone might discoverthem from scratch. Along the way we'll return repeatedly to the fourfundamental equations, and as you deepen your understanding thoseequations will come to seem comfortable and, perhaps, even beautifuland natural.

An equation for the error in the output layer, δL

:The components of δL are given by

δLj=∂C∂aLjσ′(zLj).(BP1)

This is a very natural expression. The first term on the right, ∂C/∂aLj , just measures how fast the cost ischanging as a function of the jth output activation. If, forexample, C doesn't depend much on a particular output neuron, j ,then δLj will be small, which is what we'd expect. Thesecond term on the right, σ′(zLj) , measures how fast theactivation function σ is changing at zLj

.

Notice that everything in (BP1) is easily computed. Inparticular, we compute zLj

while computing the behaviour of thenetwork, and it's only a small additional overhead to compute σ′(zLj) . The exact form of ∂C/∂aLj will, of course, depend on the form of the cost function. However,provided the cost function is known there should be little troublecomputing ∂C/∂aLj . For example, if we're usingthe quadratic cost function then C=12∑j(yj−aj)2 ,and so ∂C/∂aLj=(aj−yj)

, which obviously iseasily computable.

Equation (BP1) is a componentwise expression for δL

.It's a perfectly good expression, but not the matrix-based form wewant for backpropagation. However, it's easy to rewrite the equationin a matrix-based form, as

δL=∇aC⊙σ′(zL).(BP1a)

Here, ∇aC is defined to be a vector whose components are thepartial derivatives ∂C/∂aLj . You can think of ∇aC as expressing the rate of change of C with respect tothe output activations. It's easy to see that Equations (BP1a)and (BP1) are equivalent, and for that reason from now on we'lluse (BP1) interchangeably to refer to both equations. As anexample, in the case of the quadratic cost we have ∇aC=(aL−y) , and so the fully matrix-based form of (BP1) becomes

δL=(aL−y)⊙σ′(zL).(30)

As you can see, everything in this expression has a nice vector form,and is easily computed using a library such as Numpy.

An equation for the error δl

in terms of the error in the next layer, δl+1 : In particular

δl=((wl+1)Tδl+1)⊙σ′(zl),(BP2)

where (wl+1)T is the transpose of the weight matrix wl+1 forthe (l+1)th layer. This equation appears complicated, buteach element has a nice interpretation. Suppose we know the error δl+1 at the l+1th layer. When we apply thetranspose weight matrix, (wl+1)T , we can think intuitively ofthis as moving the error backward through the network, givingus some sort of measure of the error at the output of the lth layer. We then take the Hadamard product ⊙σ′(zl) . Thismoves the error backward through the activation function in layer l ,giving us the error δl in the weighted input to layer l

.

By combining (BP2) with (BP1) we can compute the error δl

for any layer in the network. We start byusing (BP1) to compute δL , then applyEquation (BP2) to compute δL−1 , thenEquation (BP2) again to compute δL−2

, and so on, allthe way back through the network.

An equation for the rate of change of the cost with respect to any bias in the network: In particular:

∂C∂blj=δlj.(BP3)

That is, the error δlj is exactly equal to the rate ofchange ∂C/∂blj . This is great news, since (BP1) and (BP2) have already told us how to compute δlj . We can rewrite (BP3) in shorthand as

∂C∂b=δ,(31)

where it is understood that δ is being evaluated at the sameneuron as the bias b

.

An equation for the rate of change of the cost with respect to any weight in the network: In particular:

∂C∂wljk=al−1kδlj.(BP4)

This tells us how to compute the partial derivatives ∂C/∂wljk in terms of the quantities δl and al−1 , which we already know how to compute. The equation can berewritten in a less index-heavy notation as

∂C∂w=ainδout,(32)

where it's understood that ain is the activation of theneuron input to the weight w , and δout is the error ofthe neuron output from the weight w . Zooming in to look at just theweight w

, and the two neurons connected by that weight, we candepict this as:

A nice consequence of Equation (32) isthat when the activation ain is small, ain≈0 , the gradient term ∂C/∂w will also tend to besmall. In this case, we'll say the weight learns slowly,meaning that it's not changing much during gradient descent. In otherwords, one consequence of (BP4) is that weights output fromlow-activation neurons learn slowly.

There are other insights along these lines which can be obtainedfrom (BP1)-(BP4). Let's start by looking at the outputlayer. Consider the term σ′(zLj)

in (BP1). Recallfrom the graph of the sigmoid function in the last chapter that the σ function becomesvery flat when σ(zLj) is approximately 0 or 1 . When thisoccurs we will have σ′(zLj)≈0 . And so the lesson isthat a weight in the final layer will learn slowly if the outputneuron is either low activation ( ≈0 ) or high activation( ≈1

). In this case it's common to say the output neuron hassaturated and, as a result, the weight has stopped learning (oris learning slowly). Similar remarks hold also for the biases ofoutput neuron.

We can obtain similar insights for earlier layers. In particular,note the σ′(zl)

term in (BP2). This means that δlj is likely to get small if the neuron is near saturation.And this, in turn, means that any weights input to a saturated neuronwill learn slowly* *This reasoning won't hold if wl+1Tδl+1 has large enough entries to compensate for the smallness of σ′(zlj)

. But I'm speaking of the general tendency..

Summing up, we've learnt that a weight will learn slowly if either theinput neuron is low-activation, or if the output neuron has saturated,i.e., is either high- or low-activation.

None of these observations is too greatly surprising. Still, theyhelp improve our mental model of what's going on as a neural networklearns. Furthermore, we can turn this type of reasoning around. Thefour fundamental equations turn out to hold for any activationfunction, not just the standard sigmoid function (that's because, aswe'll see in a moment, the proofs don't use any special properties of σ

). And so we can use these equations to designactivation functions which have particular desired learningproperties. As an example to give you the idea, suppose we were tochoose a (non-sigmoid) activation function σ so that σ′

is always positive, and never gets close to zero. That would preventthe slow-down of learning that occurs when ordinary sigmoid neuronssaturate. Later in the book we'll see examples where this kind ofmodification is made to the activation function. Keeping the fourequations (BP1)-(BP4) in mind can help explain why suchmodifications are tried, and what impact they can have.

Problem

• Alternate presentation of the equations of backpropagation: I've stated the equations of backpropagation (notably (BP1) and (BP2)) using the Hadamard product. This presentation may be disconcerting if you're unused to the Hadamard product. There's an alternative approach, based on conventional matrix multiplication, which some readers may find enlightening. (1) Show that (BP1) may be rewritten as
  δL=Σ′(zL)∇aC,(33)

where Σ′(zL) is a square matrix whose diagonal entries are the values σ′(zLj) , and whose off-diagonal entries are zero. Note that this matrix acts on ∇aC by conventional matrix multiplication. (2) Show that (BP2) may be rewritten as

δl=Σ′(zl)(wl+1)Tδl+1.(34)

(3) By combining observations (1) and (2) show that

δl=Σ′(zl)(wl+1)T…Σ′(zL−1)(wL)TΣ′(zL)∇aC(35)

• For readers comfortable with matrix multiplication this equation may be easier to understand than (BP1) and (BP2). The reason I've focused on (BP1) and (BP2) is because that approach turns out to be faster to implement numerically.

Proof of the four fundamental equations (optional)

We'll now prove the four fundamentalequations (BP1)-(BP4). All four are consequences of thechain rule from multivariable calculus. If you're comfortable withthe chain rule, then I strongly encourage you to attempt thederivation yourself before reading on.

Let's begin with Equation (BP1), which gives an expression forthe output error, δL

. To prove this equation, recall that bydefinition

δLj=∂C∂zLj.(36)

Applying the chain rule, we can re-express the partial derivativeabove in terms of partial derivatives with respect to the outputactivations,

δLj=∑k∂C∂aLk∂aLk∂zLj,(37)

where the sum is over all neurons k in the output layer. Of course,the output activation aLk of the kth neuron depends onlyon the input weight zLj for the jth neuron when k=j .And so ∂aLk/∂zLj vanishes when k≠j . Asa result we can simplify the previous equation to

δLj=∂C∂aLj∂aLj∂zLj.(38)

Recalling that aLj=σ(zLj) the second term on the rightcan be written as σ′(zLj) , and the equation becomes

δLj=∂C∂aLjσ′(zLj),(39)

which is just (BP1), in component form.

Next, we'll prove (BP2), which gives an equation for the error δl

in terms of the error in the next layer, δl+1 .To do this, we want to rewrite δlj=∂C/∂zlj in terms of δl+1k=∂C/∂zl+1k .We can do this using the chain rule,

δlj===∂C∂zlj∑k∂C∂zl+1k∂zl+1k∂zlj∑k∂zl+1k∂zljδl+1k,(40)(41)(42)

where in the last line we have interchanged the two terms on theright-hand side, and substituted the definition of δl+1k .To evaluate the first term on the last line, note that

zl+1k=∑jwl+1kjalj+bl+1k=∑jwl+1kjσ(zlj)+bl+1k.(43)

Differentiating, we obtain

∂zl+1k∂zlj=wl+1kjσ′(zlj).(44)

Substituting back into (42) we obtain

δlj=∑kwl+1kjδl+1kσ′(zlj).(45)

This is just (BP2) written in component form.

The final two equations we want to prove are (BP3)and (BP4). These also follow from the chain rule, in a mannersimilar to the proofs of the two equations above. I leave them to youas an exercise.

Exercise

• Prove Equations (BP3) and (BP4).

That completes the proof of the four fundamental equations ofbackpropagation. The proof may seem complicated. But it's reallyjust the outcome of carefully applying the chain rule. A little lesssuccinctly, we can think of backpropagation as a way of computing thegradient of the cost function by systematically applying the chainrule from multi-variable calculus. That's all there really is tobackpropagation - the rest is details.

The backpropagation algorithm

The backpropagation equations provide us with a way of computing thegradient of the cost function. Let's explicitly write this out in theform of an algorithm:

1. Input x

: Set the corresponding activation a1

for the input layer.

Feedforward: For each l=2,3,…,L compute zl=wlal−1+bl and al=σ(zl)

.

Output error δL : Compute the vector δL=∇aC⊙σ′(zL)

.

Backpropagate the error: For each l=L−1,L−2,…,2 compute δl=((wl+1)Tδl+1)⊙σ′(zl)

.

Output: The gradient of the cost function is given by ∂C∂wljk=al−1kδlj and ∂C∂blj=δlj

1. .

Examining the algorithm you can see why it's calledbackpropagation. We compute the error vectors δl

backward, starting from the final layer. It may seem peculiar thatwe're going through the network backward. But if you think about theproof of backpropagation, the backward movement is a consequence ofthe fact that the cost is a function of outputs from the network. Tounderstand how the cost varies with earlier weights and biases we needto repeatedly apply the chain rule, working backward through thelayers to obtain usable expressions.

Exercises

• Backpropagation with a single modified neuron Suppose we modify a single neuron in a feedforward network so that the output from the neuron is given by f(∑jwjxj+b)

, where f

is some function other than the sigmoid. How should we modify the backpropagation algorithm in this case?

Backpropagation with linear neurons Suppose we replace the usual non-linear σ function with σ(z)=z

• throughout the network. Rewrite the backpropagation algorithm for this case.

As I've described it above, the backpropagation algorithm computes thegradient of the cost function for a single training example, C=Cx

. In practice, it's common to combine backpropagation with alearning algorithm such as stochastic gradient descent, in which wecompute the gradient for many training examples. In particular, givena mini-batch of m

training examples, the following algorithm appliesa gradient descent learning step based on that mini-batch:

1. Input a set of training examples
2. For each training example x

: Set the corresponding input activation ax,1 , and perform the following steps:

• Feedforward: For each l=2,3,…,L

compute zx,l=wlax,l−1+bl and ax,l=σ(zx,l)

.

Output error δx,L : Compute the vector δx,L=∇aCx⊙σ′(zx,L)

.

Backpropagate the error: For each l=L−1,L−2,…,2 compute δx,l=((wl+1)Tδx,l+1)⊙σ′(zx,l)

• .

Gradient descent: For each l=L,L−1,…,2 update the weights according to the rule wl→wl−ηm∑xδx,l(ax,l−1)T , and the biases according to the rule bl→bl−ηm∑xδx,l

1. .

Of course, to implement stochastic gradient descent in practice youalso need an outer loop generating mini-batches of training examples,and an outer loop stepping through multiple epochs of training. I'veomitted those for simplicity.

The code for backpropagation

Having understood backpropagation in the abstract, we can nowunderstand the code used in the last chapter to implementbackpropagation. Recall fromthat chapter that the code was contained in the update_mini_batchand backprop methods of the Network class. The code forthese methods is a direct translation of the algorithm describedabove. In particular, the update_mini_batch method updates theNetwork's weights and biases by computing the gradient for thecurrent mini_batch of training examples:

class Network(object):
...
    def update_mini_batch(self, mini_batch, eta):
        """Update the network's weights and biases by applying
        gradient descent using backpropagation to a single mini batch.
        The "mini_batch" is a list of tuples "(x, y)", and "eta"
        is the learning rate."""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        for x, y in mini_batch:
            delta_nabla_b, delta_nabla_w = self.backprop(x, y)
            nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
            nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
        self.weights = [w-(eta/len(mini_batch))*nw 
                        for w, nw in zip(self.weights, nabla_w)]
        self.biases = [b-(eta/len(mini_batch))*nb 
                       for b, nb in zip(self.biases, nabla_b)]

Most of the work is done by the linedelta_nabla_b, delta_nabla_w = self.backprop(x, y) which usesthe backprop method to figure out the partial derivatives ∂Cx/∂blj and ∂Cx/∂wljk . The backprop method follows the algorithm in thelast section closely. There is one small change - we use a slightlydifferent approach to indexing the layers. This change is made totake advantage of a feature of Python, namely the use of negative listindices to count backward from the end of a list, so, e.g.,l[-3] is the third last entry in a list l. The code forbackprop is below, together with a few helper functions, whichare used to compute the σ function, the derivative σ′ ,and the derivative of the cost function. With these inclusions youshould be able to understand the code in a self-contained way. Ifsomething's tripping you up, you may find it helpful to consultthe original description (and complete listing) of the code.

class Network(object):
...
   def backprop(self, x, y):
        """Return a tuple "(nabla_b, nabla_w)" representing the
        gradient for the cost function C_x.  "nabla_b" and
        "nabla_w" are layer-by-layer lists of numpy arrays, similar
        to "self.biases" and "self.weights"."""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        # feedforward
        activation = x
        activations = [x] # list to store all the activations, layer by layer
        zs = [] # list to store all the z vectors, layer by layer
        for b, w in zip(self.biases, self.weights):
            z = np.dot(w, activation)+b
            zs.append(z)
            activation = sigmoid(z)
            activations.append(activation)
        # backward pass
        delta = self.cost_derivative(activations[-1], y) * \
            sigmoid_prime(zs[-1])
        nabla_b[-1] = delta
        nabla_w[-1] = np.dot(delta, activations[-2].transpose())
        # Note that the variable l in the loop below is used a little
        # differently to the notation in Chapter 2 of the book.  Here,
        # l = 1 means the last layer of neurons, l = 2 is the
        # second-last layer, and so on.  It's a renumbering of the
        # scheme in the book, used here to take advantage of the fact
        # that Python can use negative indices in lists.
        for l in xrange(2, self.num_layers):
            z = zs[-l]
            sp = sigmoid_prime(z)
            delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
            nabla_b[-l] = delta
            nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
        return (nabla_b, nabla_w)

...

    def cost_derivative(self, output_activations, y):
        """Return the vector of partial derivatives \partial C_x /
        \partial a for the output activations."""
        return (output_activations-y) 

def sigmoid(z):
    """The sigmoid function."""
    return 1.0/(1.0+np.exp(-z))

def sigmoid_prime(z):
    """Derivative of the sigmoid function."""
    return sigmoid(z)*(1-sigmoid(z))

Problem

• Fully matrix-based approach to backpropagation over a mini-batch Our implementation of stochastic gradient descent loops over training examples in a mini-batch. It's possible to modify the backpropagation algorithm so that it computes the gradients for all training examples in a mini-batch simultaneously. The idea is that instead of beginning with a single input vector, x

, we can begin with a matrix X=[x1x2…xm]

• whose columns are the vectors in the mini-batch. We forward-propagate by multiplying by the weight matrices, adding a suitable matrix for the bias terms, and applying the sigmoid function everywhere. We backpropagate along similar lines. Explicitly write out pseudocode for this approach to the backpropagation algorithm. Modify network.py so that it uses this fully matrix-based approach. The advantage of this approach is that it takes full advantage of modern libraries for linear algebra. As a result it can be quite a bit faster than looping over the mini-batch. (On my laptop, for example, the speedup is about a factor of two when run on MNIST classification problems like those we considered in the last chapter.) In practice, all serious libraries for backpropagation use this fully matrix-based approach or some variant.

In what sense is backpropagation a fast algorithm?

In what sense is backpropagation a fast algorithm? To answer thisquestion, let's consider another approach to computing the gradient.Imagine it's the early days of neural networks research. Maybe it'sthe 1950s or 1960s, and you're the first person in the world to thinkof using gradient descent to learn! But to make the idea work youneed a way of computing the gradient of the cost function. You thinkback to your knowledge of calculus, and decide to see if you can usethe chain rule to compute the gradient. But after playing around abit, the algebra looks complicated, and you get discouraged. So youtry to find another approach. You decide to regard the cost as afunction of the weights C=C(w)

alone (we'll get back to the biasesin a moment). You number the weights w1,w2,… , and want tocompute ∂C/∂wj for some particular weight wj .An obvious way of doing that is to use the approximation

∂C∂wj≈C(w+ϵej)−C(w)ϵ,(46)

where ϵ>0 is a small positive number, and ej is the unitvector in the jth direction. In other words, we can estimate ∂C/∂wj by computing the cost C for two slightlydifferent values of wj , and then applyingEquation (46). The same idea will let uscompute the partial derivatives ∂C/∂b

with respectto the biases.

This approach looks very promising. It's simple conceptually, andextremely easy to implement, using just a few lines of code.Certainly, it looks much more promising than the idea of using thechain rule to compute the gradient!

Unfortunately, while this approach appears promising, when youimplement the code it turns out to be extremely slow. To understandwhy, imagine we have a million weights in our network. Then for eachdistinct weight wj

we need to compute C(w+ϵej) in orderto compute ∂C/∂wj . That means that to computethe gradient we need to compute the cost function a million differenttimes, requiring a million forward passes through the network (pertraining example). We need to compute C(w)

as well, so that's atotal of a million and one passes through the network.

What's clever about backpropagation is that it enables us tosimultaneously compute all the partial derivatives ∂C/∂wj

using just one forward pass through the network,followed by one backward pass through the network. Roughly speaking,the computational cost of the backward pass is about the same as theforward pass**This should be plausible, but it requires some analysis to make a careful statement. It's plausible because the dominant computational cost in the forward pass is multiplying by the weight matrices, while in the backward pass it's multiplying by the transposes of the weight matrices. These operations obviously have similar computational cost.. And so the total cost ofbackpropagation is roughly the same as making just two forward passesthrough the network. Compare that to the million and one forwardpasses we needed for the approach basedon (46)! And so even though backpropagationappears superficially more complex than the approach basedon (46), it's actually much, much faster.

This speedup was first fully appreciated in 1986, and it greatlyexpanded the range of problems that neural networks could solve.That, in turn, caused a rush of people using neural networks. Ofcourse, backpropagation is not a panacea. Even in the late 1980speople ran up against limits, especially when attempting to usebackpropagation to train deep neural networks, i.e., networks withmany hidden layers. Later in the book we'll see how modern computersand some clever new ideas now make it possible to use backpropagationto train such deep neural networks.

Backpropagation: the big picture

As I've explained it, backpropagation presents two mysteries. First,what's the algorithm really doing? We've developed a picture of theerror being backpropagated from the output. But can we go any deeper,and build up more intuition about what is going on when we do allthese matrix and vector multiplications? The second mystery is howsomeone could ever have discovered backpropagation in the first place?It's one thing to follow the steps in an algorithm, or even to followthe proof that the algorithm works. But that doesn't mean youunderstand the problem so well that you could have discovered thealgorithm in the first place. Is there a plausible line of reasoningthat could have led you to discover the backpropagation algorithm? Inthis section I'll address both these mysteries.

To improve our intuition about what the algorithm is doing, let'simagine that we've made a small change Δwljk

to someweight in the network, wljk

:

That change in weight will cause a change in the output activationfrom the corresponding neuron: That, in turn, will cause a change in all the activations inthe next layer: Those changes will in turn cause changes in the next layer, and thenthe next, and so on all the way through to causing a change in thefinal layer, and then in the cost function: The change ΔC in the cost is related to the change Δwljk in the weight by the equation

ΔC≈∂C∂wljkΔwljk.(47)

This suggests that a possible approach to computing ∂C∂wljk is to carefully track how a small change in wljk propagates to cause a small change in C . If we can dothat, being careful to express everything along the way in terms ofeasily computable quantities, then we should be able to compute ∂C/∂wljk .

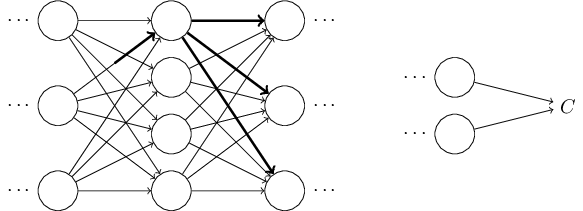
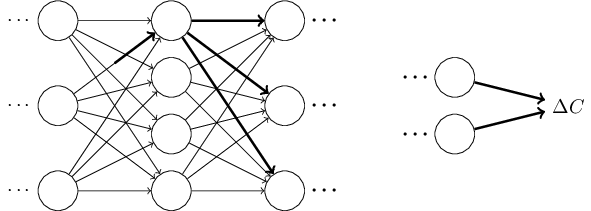
Let's try to carry this out. The change Δwljk

causes asmall change Δalj in the activation of the jth neuron inthe lth layer. This change is given by

Δalj≈∂alj∂wljkΔwljk.(48)

The change in activation Δalj will cause changes inall the activations in the next layer, i.e., the (l+1)th layer. We'll concentrate on the way just a single one of thoseactivations is affected, say al+1q

,

In fact, it'll cause the following change:

Δal+1q≈∂al+1q∂aljΔalj.(49)

Substituting in the expression from Equation (48),we get:

Δal+1q≈∂al+1q∂alj∂alj∂wljkΔwljk.(50)

Of course, the change Δal+1q will, in turn, cause changesin the activations in the next layer. In fact, we can imagine a pathall the way through the network from wljk to C , with eachchange in activation causing a change in the next activation, and,finally, a change in the cost at the output. If the path goes throughactivations alj,al+1q,…,aL−1n,aLm then theresulting expression is

ΔC≈∂C∂aLm∂aLm∂aL−1n∂aL−1n∂aL−2p…∂al+1q∂alj∂alj∂wljkΔwljk,(51)

that is, we've picked up a ∂a/∂a type term foreach additional neuron we've passed through, as well as the ∂C/∂aLm term at the end. This represents the change in C due to changes in the activations along this particular path throughthe network. Of course, there's many paths by which a change in wljk can propagate to affect the cost, and we've beenconsidering just a single path. To compute the total change in C itis plausible that we should sum over all the possible paths betweenthe weight and the final cost, i.e.,

ΔC≈∑mnp…q∂C∂aLm∂aLm∂aL−1n∂aL−1n∂aL−2p…∂al+1q∂alj∂alj∂wljkΔwljk,(52)

where we've summed over all possible choices for the intermediateneurons along the path. Comparing with (47) wesee that

∂C∂wljk=∑mnp…q∂C∂aLm∂aLm∂aL−1n∂aL−1n∂aL−2p…∂al+1q∂alj∂alj∂wljk.(53)

Now, Equation (53) looks complicated. However,it has a nice intuitive interpretation. We're computing the rate ofchange of C with respect to a weight in the network. What theequation tells us is that every edge between two neurons in thenetwork is associated with a rate factor which is just the partialderivative of one neuron's activation with respect to the otherneuron's activation. The edge from the first weight to the firstneuron has a rate factor ∂alj/∂wljk . Therate factor for a path is just the product of the rate factors alongthe path. And the total rate of change ∂C/∂wljk is just the sum of the rate factors of all paths from theinitial weight to the final cost. This procedure is illustrated here,for a single path:

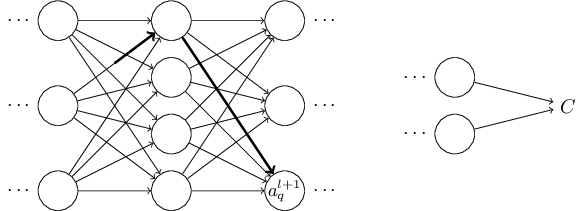
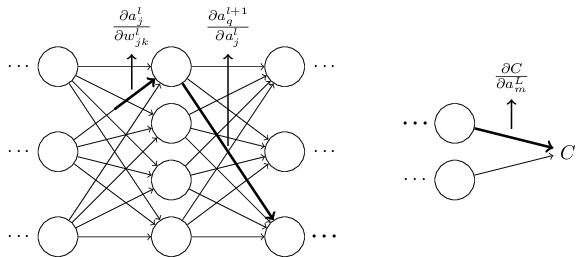
What I've been providing up to now is a heuristic argument, a way ofthinking about what's going on when you perturb a weight in a network.Let me sketch out a line of thinking you could use to further developthis argument. First, you could derive explicit expressions for allthe individual partial derivatives inEquation (53). That's easy to do with a bit ofcalculus. Having done that, you could then try to figure out how towrite all the sums over indices as matrix multiplications. This turnsout to be tedious, and requires some persistence, but notextraordinary insight. After doing all this, and then simplifying asmuch as possible, what you discover is that you end up with exactlythe backpropagation algorithm! And so you can think of thebackpropagation algorithm as providing a way of computing the sum overthe rate factor for all these paths. Or, to put it slightlydifferently, the backpropagation algorithm is a clever way of keepingtrack of small perturbations to the weights (and biases) as theypropagate through the network, reach the output, and then affect thecost.

Now, I'm not going to work through all this here. It's messy andrequires considerable care to work through all the details. If you'reup for a challenge, you may enjoy attempting it. And even if not, Ihope this line of thinking gives you some insight into whatbackpropagation is accomplishing.

What about the other mystery - how backpropagation could have beendiscovered in the first place? In fact, if you follow the approach Ijust sketched you will discover a proof of backpropagation.Unfortunately, the proof is quite a bit longer and more complicatedthan the one I described earlier in this chapter. So how was thatshort (but more mysterious) proof discovered? What you find when youwrite out all the details of the long proof is that, after the fact,there are several obvious simplifications staring you in the face.You make those simplifications, get a shorter proof, and write thatout. And then several more obvious simplifications jump out atyou. So you repeat again. The result after a few iterations is theproof we saw earlier**There is one clever step required. In Equation (53) the intermediate variables are activations like al+1q

. The clever idea is to switch to using weighted inputs, like zl+1q , as the intermediate variables. If you don't have this idea, and instead continue using the activations al+1q , the proof you obtain turns out to be slightly more complex than the proof given earlier in the chapter. - short, butsomewhat obscure, because all the signposts to its construction havebeen removed! I am, of course, asking you to trust me on this, butthere really is no great mystery to the origin of the earlier proof.It's just a lot of hard work simplifying the proof I've sketched inthis section.