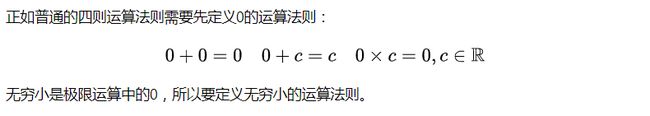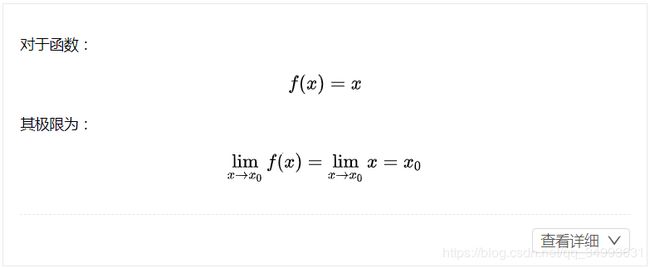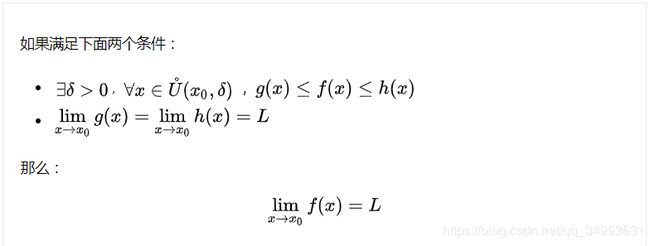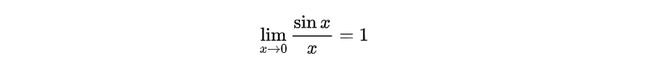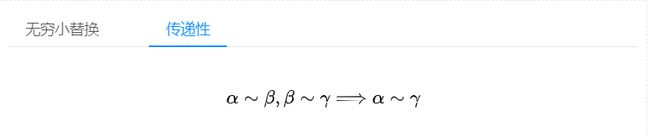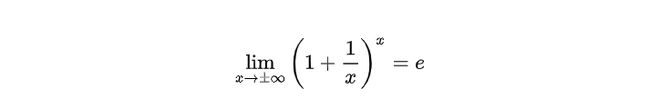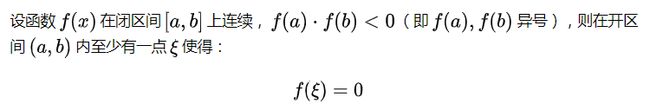微积分起源之极限&无穷&连续(《马同学高等数学》学习笔记)
微积分之极限
一切数学的工具都是为了解决问题,没有需求也就没有意义。
为什么要有个微积分
研究天文学:比如开普勒定律中会求椭圆扇形面积
计算圆的面积:时求圆面积的无限隔圆法
牛顿力学:研究运动求瞬时速度,
光学:研究光学求折射夹角
最优化问题:战争中的炮弹最优化问题,机器学习中的最优化问题,把求最优解的问题转化为判断函数的趋势的问题。
等等
这些场景都是微积分的最佳实践。
芝诺悖论与极限
芝诺悖论问题与求圆面积所使用的无限割圆法都有用到极限的概念。在芝诺版本的龟兔赛跑(其实是阿基里斯悖论这里为了方便写成了龟兔赛跑)中兔子无限的接近于乌龟,在割圆法中割的边越多多边形的面积越接近于圆的面积。这里有一个颠覆性的认知,当上述两者的自变量的坐标趋向于无穷大的时候(具体来说就是兔子每一次追上乌龟的原始位置所走过的距离时构成的数列的下标与圆内接/外切正多边形的边数)我们就可以取到他们的极限。也就是这时兔子追上了乌龟,无限正内接(外切)多边形的面积恰好就是圆的面积。这里面贯穿的一个思想就是函数无限逼近一个数那么函数的极限就是这个数本身。这个也是最反直觉的地方。
阿基里斯悖论
如果得到一个比较荒谬的结论(与现实相反的结论)。可能这是一个正确的结论只是有悖于直觉。如果是错误的结论,要么是逻辑的错误,要么就是定义的错误。在这里很明显,兔子可以追上乌龟,射出去的箭是会动的,这是事实。
阿基里斯悖论,这个问题其实和我们永远走不完这1米长的路程的悖论一样。原始的悖论就是想要走过一米首先要走过原始路程的1/2,然后再走过剩下路程的1/2以此类推这一米可以分割为无限多段的位移,我们不可能在有限的时间内走完无限的位移。
下面是哲学上的解决悖论的思辩过程。上述的逻辑中没有考虑具体的时间。假设我的速度是1m/s,按照上述的说法1米的路程可以按照数列1/2,1/4,1/8无限分割下去。那么现在我让我的时间也按照这个数列分割下去。在我接下来这一秒钟我让我前1/2s的时间走过前1/2m的路程,在让我接下来的1/4的时间走过接下来的1/4m的路程以此类推。这一秒钟我走完了这一米的路程。
如果把上面的数列求和的话那么也就是调和级数了,调和级数是一个无限逼近于1但是不等于1的一个函数,也就是无论取多么大的一个正整数常数的坐标它多不会等于1,但是事实上我们真的走完了1米的路程。理论上无限逼近于1但是现实中是我们走过了1米。这就是因为我们的坐标轴是无穷大的(对应于我们1s的时间是可以分割为无穷多份的)这就是事实。所以当我们用无穷多的小的时间片走完了1m的时候,调和级数就能在在横坐标趋于无限大的时候等于1,你没有听错就是在趋于无穷大的时候等于1。从另一个角度来说无限逼近于1的函数与就是1之间似乎差了一个东西那就是无穷小,需要注意的是当坐标轴趋向于无穷大的时候无穷小的极限就是0。结论就是调和数列取极限就是1。这就是事实,这就是自然的法则。
飞矢不动悖论
飞矢不动的错误也就是定义的错误。飞矢不动的假设就是瞬间的存在,在这个瞬间箭走过的距离是0m。但事实上这里的瞬间只是在说一个无穷小的时间,是一个无限趋近于0但是不为0的时间。在这无穷小的时间段内,箭会发生一段无穷小的位移的。接下来就是对无穷小的时间进行积分,对应的箭的位移也会发生累加,最后的结果就是箭发生了肉眼可见的位移。
另一个角度,飞矢不动假定瞬间的存在,那么箭想要发生位移的话必须是从这个瞬间的位置移动到下一个时间的位置。那么事实是在这两个瞬间之间有无穷多个无穷小的时间碎片,也就是时间不是离散的而是连续的,构成它的基本最小单位就是无穷小。(下文中会讲到无穷小不是一个固定的值而是一个函数,它可以比一个固定的极小的常数值要小,它是一个新的物种)。那么我可以这样理解,箭所经过的最小的时间单位是无穷小(再次提醒自己无穷小比任何大于0的常数都小)。箭在无穷小时间内走过的路程也是无穷小。在一段时间段内会包含无穷多个无穷小。
归结起来就是,最小的时间段就是无穷小的时间。一段常数长度的时间片内包含无穷大个无穷小的时间。无穷小的时间的位移是无穷小,这段时间走过的位移也就是无穷大的无穷小的时间所经过的位移的积分。
小结
无穷大与无穷小是一个新的物种。当函数趋于无穷的时候它的值会等于极限本身。
魏尔斯特拉斯的数列极限
柯西的极限
首先来看看柯西最早提出的极限。
若某数列无限地趋向于某一实数,与该实数的差可以任意小,则该确定的实数称为此数列的极限。
在这里有几个意思不清的地方:
什么是“无限”?
什么是“无限地趋向于”?
什么是“任意小”?
魏尔斯特拉斯的数列极限
魏尔斯特拉斯是现代分析之父,分析就是数学严格化。他把柯西的极限定义做出了严格化。
再数学化一些就是:
这里极限计算的思路很奇怪,先给定ε,然后再去证明存在一个N,进而证明了极限的存在。这里奇怪的地方在于,一般情况下习惯于从自变量到因变量的思考,但是这里我们先关注结果也就是|a - L| < ε 这个目标然后再去求有没有满足条件的N,这是一个由因变量到自变量的过程。
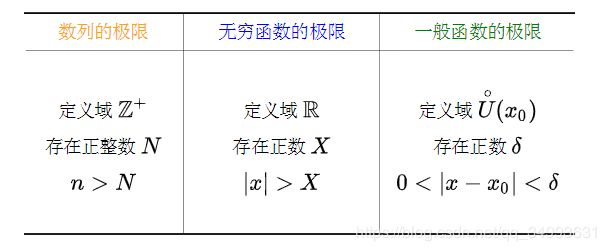
其它函数的极限都可以由数列极限拓展得到。以下为推广到一般函数时的对照表:
这里需要说明一些重要的事项,也就是我们在求一般函数的极限的时候所涉及到的定义域是去心领域,所以当求趋向于x点时的极限的时候不需要考虑函数在x点本身的情况。比如说我们在计算函数在x点左右极限的时候不需要x点本身的情况。
极限的3个性质
唯一性,若一个函数存在极限那么此极限唯一。
保号性,若一个函数在x0处的极限是大于0的,那么存在一个去心领域0 < |x - x0| < ξ使得该函数 > 0(小于0的情况也是一样的)。
有界性,若一个函数在x0处有极限,那么存在一个实数M使得f(x) < M。
无穷小与无穷大到底是什么?
无穷小的定义是这样的:
无穷大的定义是这样的:
无穷小与无穷大是函数(数列是一种特殊的函数)。因为任取一个ε > 0(ε是一个足够小的常数)无穷小都能够比它小;再来,任取一个ε > 0(ε是一个足够大的常数)无穷大都能够比它大。这就说明无穷小与无穷大都不是具体的数,它是一个变化趋势他是一个函数。这就是从初等数学到高等数学研究对象的不同,即从静态的点到动态的趋势。
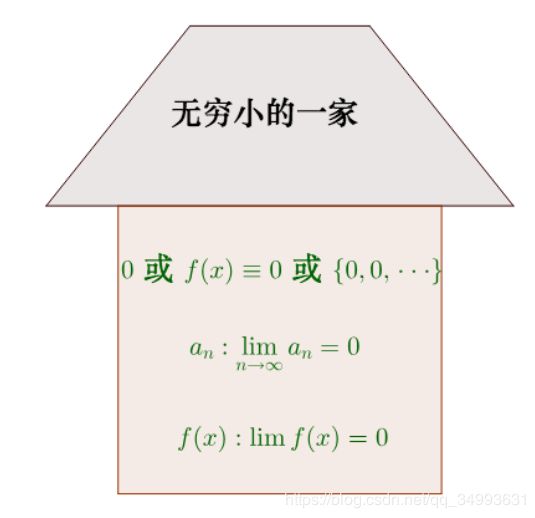
下面给出无穷小与无穷大的“家族”。
无穷小与极限的计算
无穷小与极限存在以下的关系
无穷小的理论基于极限这个公里,这里相当于是极限与无穷小的一个演绎。(啊哈,一句无用的废话)
无穷小的运算法则
极限的分配率
一个重要的极限
多项式极限的计算法则
一句话,也就是高阶的函数变化的趋势会更快,所以高阶的函数占主导地位。
复合函数的极限
0/0型的极限的计算与夹逼定理
0/0型的极限,一般不好直接求解所以一般使用夹逼定理去求解。
重要极限:
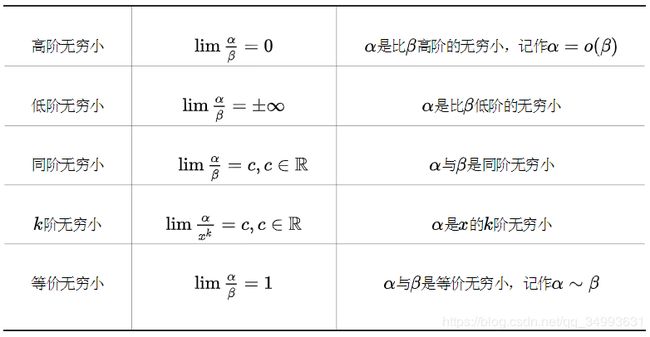
无穷小的比较与等价无穷小
无穷小的比较
无穷小的替换与传递性
几个重要的等价无穷小
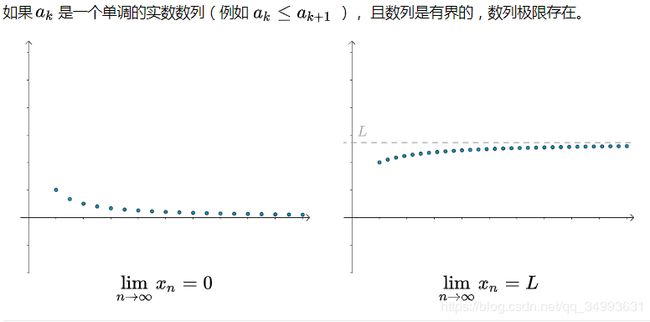
一种极限判断的方法(单调有界必有极限)
单调有界
需要注意的是这是一个充分条件,也就意味着有极限的函数不一定是单调有界的。
自然常数公式
首先证明,复利函数是单调有界的,然后再使用夹逼定理计算复利函数的极限。
连续与间断
连续
这里就体现出了阅读理解的重要性。我们先看看连续的概念:
这里需要注意这么几个点,首先我们讨论的是在函数的定义域内,最后我们讨论的连续是点的连续而非我们平常所讲的线的连续,这两点是颠覆我们认知的地方。那么根据上面的定义来看1/x也是一个连续函数。
间断
连续讨论的前提是函数在去心邻域上有定义,而间断讨论的前提是函数在去心邻域上有定义。正是因为他们讨论的前提是不同的所以对于一个函数的一个点是连续还是间断是独立的。
这里说明一下间断点与非连续函数的关系,非连续函数一定有间断点,但是有间断点的函数不一定是非连续函数。比如说1/x在0点是一个间断点,但是它是一个连续函数。这就追溯到判断一个函数连续与非连续是在定义域上判断的,但是一个函数的间断点的判断是去心邻域。在定义域内1/x就是一个连续函数,在去心邻域内它又有一个间断点。
下面给出间断点的分类:
关于连续几个重要的结论
- 基本初等函数以及他们的线性组合都是连续函数。
- 原函数为单调函数则存在反函数。
- 原函数存在反函数则原函数的单调性与反函数的单调性一致。
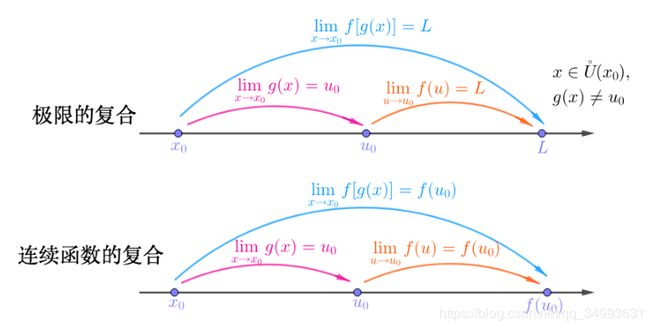
复合函数的连续性
这里需要注意的是:
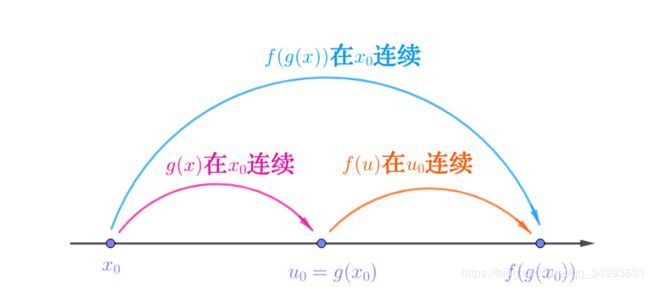
极限的复合是针对于一般函数的(也就是在某一点的去心领域有定义),但是连续函数的复合是针对于连续函数的。这里需要注意极限复合中的条件也就是在去心邻域内函数值不等于极限,如果无论如何都找不到这样的领域的话那么这个函数的复合极限是不存在的。那么复合函数连续的条件也就是:
闭区间连续
这里说明一下间断连续,间断函数与连续函数的定义是有所不同的。比如函数1/x是一个连续函数,因为连续函数的判断是在定义域上进行判定的。但是1/x有一个间断点,间断点考虑的是去心邻域。而闭区间连续又是在给定区间上考虑的那么1/x在[-1,1]上面是间断的。下面引出闭区间连续的定义:
同时也有一个重要的结论:在闭区间上连续的函数在该区间上有界,且一定能取得它的最大值和最小值。
零点定理与介值定理
闭区间连续与零点定理与介值定理是一种递进的关系。
零点定理
介值定理
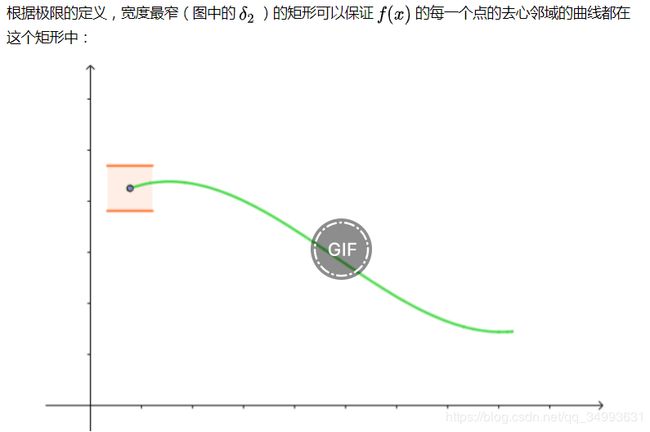
一致性连续
一致性连续是一种比较严格的连续。也就是在一个闭区间上最强的约束δ能够满足其他所有宽松的约束。
总结
最后,本篇博客为《马同学高等数学》的学习笔记,如有侵权请联系我马上修改。