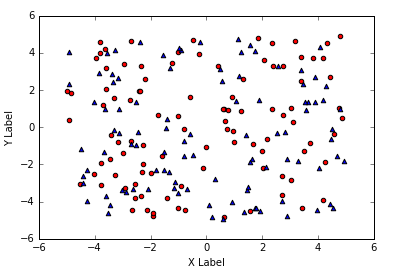
猜数字游戏代码:importrandomdefpythonit():a=random.randint(1,100)n=int(input("输入你猜想的数字:"))whilen!=a:ifn>a:print("很遗憾,猜大了")n=int(input("请再次输入你猜想的数字:"))elifna::如果玩家猜的数字n大于随机数字a,则输出"很遗憾,猜大了",并提示玩家再次输入。elifn
基于Google authentic实现的双因子登录认证系统前后台基于SSMP+Vue+Element(解决SecureRandom造成的服务器请求缓慢)
Tate_Brown
gitJAVAIDEADEBUGVUE
用md5两次加盐密码,可以灵活更换算法--直接上代码地址:JAVA后台:https://github.com/TateBrownJava/TwoFALogindemoBackendVue前端:https://github.com/TateBrownJava/TwoFALoginDemofrontend-------------------------------------------------
Open3D 使用RANSAC分割平面
今夕是何年,
单目+双目计算机视觉
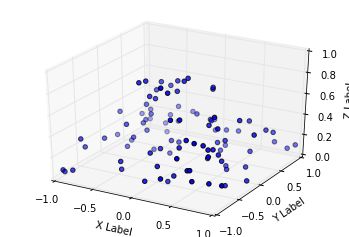
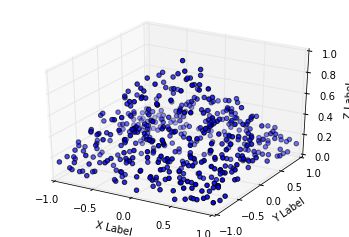
目录1,概述2,拟合平面3,实现过程4,主要函数:defsegment_plane(self,distance_threshold,ransac_n,num_iterations):'''5,代码实现6,结果展示1,概述随机抽样一致性算法QRANSAC(Randomsampleconsensus)是一种迭代的方法来从一系列包含有离异值的数据中计算数学模型参数的方法。RANSAC算法本质上由两步组成
groupby 中如何显示 tqdm 的进度条?
domodo2020
在循环时调用tqdm显示进度已经是一个常规操作,常见的方式是foriiintqdm(...):...while循环的情况类似,whileicntintqdm(range(n)):...icnt+=1这里记录没有显式循环时,在groupby中的用法:importpandasaspdimportnumpyasnpfromtqdmimporttqdmdf=pd.DataFrame(np.random.r
Python——俄罗斯方块
星和月
pythonpygame开发语言
俄罗斯方块游戏是一款经典的益智游戏,通常使用编程语言Python来实现。下面是一个简单的俄罗斯方块游戏的示例代码:importpygameimportrandom#定义颜色BLACK=(0,0,0)WHITE=(255,255,255)RED=(255,0,0)GREEN=(0,255,0)BLUE=(0,0,255)CYAN=(0,255,255)MAGENTA=(255,0,255)YELLO
python有趣游戏代码大全
uolo_python
游戏
一.贪吃蛇运行以下代码,将会弹出一个窗口显示贪吃蛇游戏。你可以使用箭头键控制贪吃蛇的移动。吃到食物后蛇的长度会增加,如果蛇触碰到边界或者自己则游戏结束。按下Q键退出游戏,按下C键重新开始游戏。importpygameimportrandom#初始化pygame.init()#设置游戏窗口window_width,window_height=640,480window=pygame.display.
MySQL连接层-(通讯协议-线程-验证)
否极泰来+
mysql
通讯协议通讯协议连接方式所支持的操作系统TCP/IPlocal,remoteAIISocketfilelocalUNIX-derivedoperatingsystemsincludingLinux,BSD,MaxOSXSharedmemorylocalWindowsNamedpipeslocalWindows1.TCP/IP(传输控制协议/互联网协议):-是用于连接互联网上主机的一套通信协议-使用
python数组的基本操作
迟遇3
python开发语言
一.创建数组arr:list[int]=[0]*8num1:list[int]=[1,5,9,8,6]二.访问元素1.指定访问(通过索引(下标))defrandom_a(nums:list[int])->int:returnnums[2]print(random_a(arr))2.随机访问(会访问不同的元素)defrandom_access(nums:list[int])->int:"""随机访问
概率图模型(PGM)综述
医学影像处理
概率图模型概率图模型综述
RefLink:http://www.sigvc.org/bbs/thread-728-1-1.htmlGraphicalModel的基本类型基本的GraphicalModel可以大致分为两个类别:贝叶斯网络(BayesianNetwork)和马尔可夫随机场(MarkovRandomField)。它们的主要区别在于采用不同类型的图来表达变量之间的关系:贝叶斯网络采用有向无环图(DirectedAc
qt 创建随机数
入梦游
qt
qt中有两种创建随机数的方法,一种是旧方法,一种是新方法目录旧方法:已过时intqrand()voidqsrand(uintseed)Example新方法QRandomGenerator::global()->bouned(inthighest)QRandomGenerator::global()->generate()更多旧方法:已过时intqrand()生成一个伪随机数,可以使用qsrand(
C++ STL概念之 算法
元凌丶
算法c++开发语言
sortdefault(1)templatevoidsort(RandomAccessIteratorfirst,RandomAccessIteratorlast);custom(2)templatevoidsort(RandomAccessIteratorfirst,RandomAccessIteratorlast,Comparecomp);作用:用于对容器中的元素进行排序。它通常采用快速排序算
YOLOv8数据增强
热心小张
研究生yolov8
1.找到augment.py(ultralytics/data/augment.py),修改对应内容#TransformsT=[A.Blur(p=0.01),A.MedianBlur(p=0.01),A.ToGray(p=0.01),A.CLAHE(p=0.01),A.RandomBrightnessContrast(p=0.0),A.RandomGamma(p=0.0),A.ImageCompr
计算机视觉中的数据增强方法总结
CV技术指南(公众号)
CV技术总结计算机视觉深度学习卷积神经网络
前言:在计算机视觉方向,数据增强的本质是人为地引入人视觉上的先验知识,可以很好地提升模型的性能,目前基本成为模型的标配。最近几年逐渐出了很多新的数据增强方法,在本文将对数据增强做一个总结。本文介绍了数据增强的作用,数据增强的分类,数据增强的常用方法,一些特殊的方法,如Cutout,RandomErasing,Mixup,Hide-and-Seek,CutMix,GridMask,FenceMask
基于VGG的猫狗识别
卑微小鹿
tensorflowtensorflow
由于猫和狗的数据在这里,所以就做了一下分类的神经网络1、首先进行图像处理:importcsvimportglobimportosimportrandomos.environ['TF_CPP_MIN_LOG_LEVEL']='2'importtensorflowastffromtensorflowimportkerasfromtensorflow.kerasimportlayersimportnum
RAM(随机存取存储器)都有哪些?(超详细)
嵌入式-JY老师
嵌入式工程师c语言硬件架构智能硬件嵌入式硬件
目录RAM的特点RAM的类型1.SRAM(静态随机存取存储器)2.DRAM(动态随机存取存储器)3.SDRAM(同步动态随机存取存储器)4.DDRSDRAM(双倍数据速率同步动态随机存取存储器)5.RDRAM(Rambus动态随机存取存储器)6.VRAM(视频随机存取存储器)7.MRAM(磁阻随机存取存储器)8.FeRAM(铁电随机存取存储器)RAM(RandomAccessMemory,随机存取
使用爬虫写一个简易的翻译器+图像界面+python
w²大大
python学习pythontkinterjson
翻译器+图像界面+python1.效果图如下:2.代码实现1.效果图如下:2.代码实现importtkinterimportrandomimportrequestsimportrequestimporturllibfromurllibimportrequest,parseimporttime,json,random,hashlibwin=tkinter.Tk()defpachong():try:u
Python小游戏——雷霆战机
星和月
pygamepython开发语言
importpygameimportrandom#初始化pygame.init()#定义游戏窗口大小window_width=800window_height=600#创建游戏窗口window=pygame.display.set_mode((window_width,window_height))pygame.display.set_caption("雷霆战机")#加载图片player_img=
JS笔记
陈两全
笔记
9.111.Math对象Math对象属于Javascript内置对象,无需实例化(不需要添加new),可以直接使用。只有一个Math.PI的属性1.1.Math对象的方法Math.round(number)//四舍五入整数Math.ceil(number)//向上取整Math.floor(number)//向下取整Math.random()//随机返回0.0~1.0之间的数Math.max(x,y
网络安全 L1 Introduction to Security
h08.14
网络安全web安全安全
Informationsecurity1.Theprocessofpreventinganddetectingunauthoriseduseofyourinformation.2.Thescienceofguardinginformationsystemsandassetsagainstmaliciousbehavioursofintelligentadversaries.3.Securityvs
力扣LeetCode-栈和队列
流忆,留宜
LeetCodeleetcodec++算法
栈与队列基本知识C++标准库有很多版本,三个最为普遍的STL版本HPSTL其他版本的C++STL,一般是以HPSTL为蓝本实现出来的,HPSTL是C++STL的第一个实现版本,而且开放源代码。P.J.PlaugerSTL由P.J.Plauger参照HPSTL实现出来的,被VisualC++编译器所采用,不是开源的。SGISTL由SiliconGraphicsComputerSystems公司参照H
【python】【Ray的概述】
资源存储库
python开发语言
Overview概述Rayisanopen-sourceunifiedframeworkforscalingAIandPythonapplicationslikemachinelearning.Itprovidesthecomputelayerforparallelprocessingsothatyoudon’tneedtobeadistributedsystemsexpert.Rayminimi
[学习笔记]《CSAPP》深入理解计算机系统 - Chapter 6 存储器层次结构
Artintel
学习学习笔记ccsapp
总结一些第六章的一些关键信息Chapter6存储器层次结构DMA局部性抖动Chapter6存储器层次结构随机访问存储器(Random-AccessMemory,RAM)分为两类:静态的和动态的。静态(SRAM)比动态更快,更贵动态(DRAM)数据流通过称为总线(bus)的共享电子电路在处理器和DRAM主存来来回回。每次CPU和主存之间的数据传送都是通过一系列的步骤来完成的,这些步骤称为总线事务(b
js实现动态生成不固定数量的气泡
小丁冲鸭!
javascript前端开发语言
样式:核心代码:1、添加气泡的方法addCircle(){letheight=645;letwidth=312;letminSize=38;letmaxSize=78;letnewCircle={x:Math.random()*width,//随机位置,留出边界y:Math.random()*height,size:(minSize+Math.random()*(maxSize-minSize+1
膨胀腐蚀操作opencv dilate膨胀白膨胀,erode腐蚀是黑吃白。主要针对二值图
tony365
opencv人工智能计算机视觉
效果:代码:importcv2importnumpyasnpfrommatplotlibimportpyplotaspltif__name__=="__main__":h=10w=10data=np.random.normal(0,1,[h,w])#sigma,2*sigma,3*sigma之间的数的比例分别为0.68,0.96,0.99mask_new=data>2print(data)prin
蒙特卡罗——三门问题python代码实现
潮汐退涨月冷风霜
python开发语言蒙特卡罗
三门问题b站李永乐老师讲解三门问题python蒙特卡罗模拟#模拟三门问题importrandomasrd#n:模拟次数,m:中奖次数n=100000m=0foriinrange(n):#车位于的门号car=rd.randint(0,2)#人随机选择一个门door=rd.randint(0,2)#主持人展示空门empties={0,1,2}-{car,door}empty=rd.choice(lis
SDN系统方法 | 7. 叶棘网络
DeepNoMind
随着互联网和数据中心流量的爆炸式增长,SDN已经逐步取代静态路由交换设备成为构建网络的主流方式,本系列是免费电子书《Software-DefinedNetworks:ASystemsApproach》的中文版,完整介绍了SDN的概念、原理、架构和实现方式。原文:Software-DefinedNetworks:ASystemsApproach第7章叶棘网络(Leaf-SpineFabric)本章介
python爬虫处理滑块验证_python selenium爬虫滑块验证
用户6731453637
python爬虫处理滑块验证
importrandomimporttimefromPILimportImagefromioimportBytesIOimportrequestsasrqfrombs4importBeautifulSoupasbsfromseleniumimportwebdriverfromselenium.webdriverimportActionChainsfromselenium.webdriverimpo
Python代码雨
镜花照无眠
#Python
importrandomimportpygameimportsys#初始化参数设计win_width=1000win_height=800font_px=15#创建窗口及文本设计pygame.init()winsur=pygame.display.set_mode((win_width,win_height))font=pygame.font.SysFont('',23)bg_surface=py
蒙特卡罗方法——布丰投针实验近似计算圆周率python代码实现
潮汐退涨月冷风霜
python开发语言蒙特卡罗
布丰实验数学原理python代码importrandomasrdimportnumpyasnpimportmathimportmatplotlib.pyplotaspltimportmatplotlibmatplotlib.rcParams['font.family']='SimHei'#或者'MicrosoftYaHei'matplotlib.rcParams['axes.unicode_min
Day05for和while
PythonLi
1.如果是不断的获取序列中的元素,直接使用for循环2.如果循环次数确定,最好也使用for循环3.死循环和循环次数不确定的时候最好使用while循环。练习:随机产生一个数字(0,100),不断的输入数字,直到输入的数字和产生的随机数相同为止如果猜错了提示大了或者小importrandom产生一个随机数number=random.randint(0,100)返回从键盘接受到的数据(输入的时候以回车结
多线程编程之存钱与取钱
周凡杨
javathread多线程存钱取钱
生活费问题是这样的:学生每月都需要生活费,家长一次预存一段时间的生活费,家长和学生使用统一的一个帐号,在学生每次取帐号中一部分钱,直到帐号中没钱时 通知家长存钱,而家长看到帐户还有钱则不存钱,直到帐户没钱时才存钱。
问题分析:首先问题中有三个实体,学生、家长、银行账户,所以设计程序时就要设计三个类。其中银行账户只有一个,学生和家长操作的是同一个银行账户,学生的行为是
java中数组与List相互转换的方法
征客丶
JavaScriptjavajsonp
1.List转换成为数组。(这里的List是实体是ArrayList)
调用ArrayList的toArray方法。
toArray
public T[] toArray(T[] a)返回一个按照正确的顺序包含此列表中所有元素的数组;返回数组的运行时类型就是指定数组的运行时类型。如果列表能放入指定的数组,则返回放入此列表元素的数组。否则,将根据指定数组的运行时类型和此列表的大小分
Shell 流程控制
daizj
流程控制if elsewhilecaseshell
Shell 流程控制
和Java、PHP等语言不一样,sh的流程控制不可为空,如(以下为PHP流程控制写法):
<?php
if(isset($_GET["q"])){
search(q);}else{// 不做任何事情}
在sh/bash里可不能这么写,如果else分支没有语句执行,就不要写这个else,就像这样 if else if
if 语句语
Linux服务器新手操作之二
周凡杨
Linux 简单 操作
1.利用关键字搜寻Man Pages man -k keyword 其中-k 是选项,keyword是要搜寻的关键字 如果现在想使用whoami命令,但是只记住了前3个字符who,就可以使用 man -k who来搜寻关键字who的man命令 [haself@HA5-DZ26 ~]$ man -k
socket聊天室之服务器搭建
朱辉辉33
socket
因为我们做的是聊天室,所以会有多个客户端,每个客户端我们用一个线程去实现,通过搭建一个服务器来实现从每个客户端来读取信息和发送信息。
我们先写客户端的线程。
public class ChatSocket extends Thread{
Socket socket;
public ChatSocket(Socket socket){
this.sock
利用finereport建设保险公司决策分析系统的思路和方法
老A不折腾
finereport金融保险分析系统报表系统项目开发
决策分析系统呈现的是数据页面,也就是俗称的报表,报表与报表间、数据与数据间都按照一定的逻辑设定,是业务人员查看、分析数据的平台,更是辅助领导们运营决策的平台。底层数据决定上层分析,所以建设决策分析系统一般包括数据层处理(数据仓库建设)。
项目背景介绍
通常,保险公司信息化程度很高,基本上都有业务处理系统(像集团业务处理系统、老业务处理系统、个人代理人系统等)、数据服务系统(通过
始终要页面在ifream的最顶层
林鹤霄
index.jsp中有ifream,但是session消失后要让login.jsp始终显示到ifream的最顶层。。。始终没搞定,后来反复琢磨之后,得到了解决办法,在这儿给大家分享下。。
index.jsp--->主要是加了颜色的那一句
<html>
<iframe name="top" ></iframe>
<ifram
MySQL binlog恢复数据
aigo
mysql
1,先确保my.ini已经配置了binlog:
# binlog
log_bin = D:/mysql-5.6.21-winx64/log/binlog/mysql-bin.log
log_bin_index = D:/mysql-5.6.21-winx64/log/binlog/mysql-bin.index
log_error = D:/mysql-5.6.21-win
OCX打成CBA包并实现自动安装与自动升级
alxw4616
ocxcab
近来手上有个项目,需要使用ocx控件
(ocx是什么?
http://baike.baidu.com/view/393671.htm)
在生产过程中我遇到了如下问题.
1. 如何让 ocx 自动安装?
a) 如何签名?
b) 如何打包?
c) 如何安装到指定目录?
2.
Hashmap队列和PriorityQueue队列的应用
百合不是茶
Hashmap队列PriorityQueue队列
HashMap队列已经是学过了的,但是最近在用的时候不是很熟悉,刚刚重新看以一次,
HashMap是K,v键 ,值
put()添加元素
//下面试HashMap去掉重复的
package com.hashMapandPriorityQueue;
import java.util.H
JDK1.5 returnvalue实例
bijian1013
javathreadjava多线程returnvalue
Callable接口:
返回结果并且可能抛出异常的任务。实现者定义了一个不带任何参数的叫做 call 的方法。
Callable 接口类似于 Runnable,两者都是为那些其实例可能被另一个线程执行的类设计的。但是 Runnable 不会返回结果,并且无法抛出经过检查的异常。
ExecutorService接口方
angularjs指令中动态编译的方法(适用于有异步请求的情况) 内嵌指令无效
bijian1013
JavaScriptAngularJS
在directive的link中有一个$http请求,当请求完成后根据返回的值动态做element.append('......');这个操作,能显示没问题,可问题是我动态组的HTML里面有ng-click,发现显示出来的内容根本不执行ng-click绑定的方法!
【Java范型二】Java范型详解之extend限定范型参数的类型
bit1129
extend
在第一篇中,定义范型类时,使用如下的方式:
public class Generics<M, S, N> {
//M,S,N是范型参数
}
这种方式定义的范型类有两个基本的问题:
1. 范型参数定义的实例字段,如private M m = null;由于M的类型在运行时才能确定,那么我们在类的方法中,无法使用m,这跟定义pri
【HBase十三】HBase知识点总结
bit1129
hbase
1. 数据从MemStore flush到磁盘的触发条件有哪些?
a.显式调用flush,比如flush 'mytable'
b.MemStore中的数据容量超过flush的指定容量,hbase.hregion.memstore.flush.size,默认值是64M 2. Region的构成是怎么样?
1个Region由若干个Store组成
服务器被DDOS攻击防御的SHELL脚本
ronin47
mkdir /root/bin
vi /root/bin/dropip.sh
#!/bin/bash/bin/netstat -na|grep ESTABLISHED|awk ‘{print $5}’|awk -F:‘{print $1}’|sort|uniq -c|sort -rn|head -10|grep -v -E ’192.168|127.0′|awk ‘{if($2!=null&a
java程序员生存手册-craps 游戏-一个简单的游戏
bylijinnan
java
import java.util.Random;
public class CrapsGame {
/**
*
*一个简单的赌*博游戏,游戏规则如下:
*玩家掷两个骰子,点数为1到6,如果第一次点数和为7或11,则玩家胜,
*如果点数和为2、3或12,则玩家输,
*如果和为其它点数,则记录第一次的点数和,然后继续掷骰,直至点数和等于第一次掷出的点
TOMCAT启动提示NB: JAVA_HOME should point to a JDK not a JRE解决
开窍的石头
JAVA_HOME
当tomcat是解压的时候,用eclipse启动正常,点击startup.bat的时候启动报错;
报错如下:
The JAVA_HOME environment variable is not defined correctly
This environment variable is needed to run this program
NB: JAVA_HOME shou
[操作系统内核]操作系统与互联网
comsci
操作系统
我首先申明:我这里所说的问题并不是针对哪个厂商的,仅仅是描述我对操作系统技术的一些看法
操作系统是一种与硬件层关系非常密切的系统软件,按理说,这种系统软件应该是由设计CPU和硬件板卡的厂商开发的,和软件公司没有直接的关系,也就是说,操作系统应该由做硬件的厂商来设计和开发
富文本框ckeditor_4.4.7 文本框的简单使用 支持IE11
cuityang
富文本框
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<meta http-equiv="Content-Type" content="text/html; charset=UTF-8" />
<title>知识库内容编辑</tit
Property null not found
darrenzhu
datagridFlexAdvancedpropery null
When you got error message like "Property null not found ***", try to fix it by the following way:
1)if you are using AdvancedDatagrid, make sure you only update the data in the data prov
MySQl数据库字符串替换函数使用
dcj3sjt126com
mysql函数替换
需求:需要将数据表中一个字段的值里面的所有的 . 替换成 _
原来的数据是 site.title site.keywords ....
替换后要为 site_title site_keywords
使用的SQL语句如下:
updat
mac上终端起动MySQL的方法
dcj3sjt126com
mysqlmac
首先去官网下载: http://www.mysql.com/downloads/
我下载了5.6.11的dmg然后安装,安装完成之后..如果要用终端去玩SQL.那么一开始要输入很长的:/usr/local/mysql/bin/mysql
这不方便啊,好想像windows下的cmd里面一样输入mysql -uroot -p1这样...上网查了下..可以实现滴.
打开终端,输入:
1
Gson使用一(Gson)
eksliang
jsongson
转载请出自出处:http://eksliang.iteye.com/blog/2175401 一.概述
从结构上看Json,所有的数据(data)最终都可以分解成三种类型:
第一种类型是标量(scalar),也就是一个单独的字符串(string)或数字(numbers),比如"ickes"这个字符串。
第二种类型是序列(sequence),又叫做数组(array)
android点滴4
gundumw100
android
Android 47个小知识
http://www.open-open.com/lib/view/open1422676091314.html
Android实用代码七段(一)
http://www.cnblogs.com/over140/archive/2012/09/26/2611999.html
http://www.cnblogs.com/over140/arch
JavaWeb之JSP基本语法
ihuning
javaweb
目录
JSP模版元素
JSP表达式
JSP脚本片断
EL表达式
JSP注释
特殊字符序列的转义处理
如何查找JSP页面中的错误
JSP模版元素
JSP页面中的静态HTML内容称之为JSP模版元素,在静态的HTML内容之中可以嵌套JSP
App Extension编程指南(iOS8/OS X v10.10)中文版
啸笑天
ext
当iOS 8.0和OS X v10.10发布后,一个全新的概念出现在我们眼前,那就是应用扩展。顾名思义,应用扩展允许开发者扩展应用的自定义功能和内容,能够让用户在使用其他app时使用该项功能。你可以开发一个应用扩展来执行某些特定的任务,用户使用该扩展后就可以在多个上下文环境中执行该任务。比如说,你提供了一个能让用户把内容分
SQLServer实现无限级树结构
macroli
oraclesqlSQL Server
表结构如下:
数据库id path titlesort 排序 1 0 首页 0 2 0,1 新闻 1 3 0,2 JAVA 2 4 0,3 JSP 3 5 0,2,3 业界动态 2 6 0,2,3 国内新闻 1
创建一个存储过程来实现,如果要在页面上使用可以设置一个返回变量将至传过去
create procedure test
as
begin
decla
Css居中div,Css居中img,Css居中文本,Css垂直居中div
qiaolevip
众观千象学习永无止境每天进步一点点css
/**********Css居中Div**********/
div.center {
width: 100px;
margin: 0 auto;
}
/**********Css居中img**********/
img.center {
display: block;
margin-left: auto;
margin-right: auto;
}
Oracle 常用操作(实用)
吃猫的鱼
oracle
SQL>select text from all_source where owner=user and name=upper('&plsql_name');
SQL>select * from user_ind_columns where index_name=upper('&index_name'); 将表记录恢复到指定时间段以前
iOS中使用RSA对数据进行加密解密
witcheryne
iosrsaiPhoneobjective c
RSA算法是一种非对称加密算法,常被用于加密数据传输.如果配合上数字摘要算法, 也可以用于文件签名.
本文将讨论如何在iOS中使用RSA传输加密数据. 本文环境
mac os
openssl-1.0.1j, openssl需要使用1.x版本, 推荐使用[homebrew](http://brew.sh/)安装.
Java 8
RSA基本原理
RS