Abstract
时间抽象是强化学习中扩大学习和规划的关键。虽然计划与时间扩展的行动是众所周知的,但从数据中自主地创建这样的抽象仍然具有挑战性。我们在option框架内解决这个问题[Sutton,Precup&Singh,1999;Precup,2000]。我们推导了option的策略梯度定理,并提出了一种新的 \(opiton\text{-}critic\) 体系结构,它能够同时学习 option 的内部策略和终止条件,并且不需要提供任何额外的奖励或子目标。在离散和连续环境下的实验结果表明了该框架的灵活性和高效性。
Temporal abstraction:
Introduction
时间抽象允许表示发生在不同时间尺度上的行为过程的知识。
How to understand? Option?
在强化学习中,option(Sutton、Precup和Singh 1999;Precup 2000)为定义此类行动方案以及与之无缝地学习和规划提供了框架。在过去的15年里,自主地发现时间抽象一直是广泛研究的主题(McGovern和Barto 2001;Stolle和Precup 2002;Menache、Mannor和Shimkin 2002;S¸ims¸ek和Barto 2009;Silver和Ciosek 2012),但是可以自然地与连续状态和/或动作空间一起使用的方法直到最近才开始变得可行(Konidaris等人。2011年;Niekum 2013年;Mann、Mannor和Precup 2015年;Mankowitz、Mann和Mannor 2016年;Kulkarni等人。2016年;V ezhnevets等人。2016年;Daniel等人。2016年)。
现有的大部分工作都集中在寻找子目标(代理应该达到的有用状态)以及随后学习实现这些目标的策略。这一想法导致了有趣的方法,但因为他们的 "combinatorial" flavor 也很难扩大规模,。此外,与子目标相关的策略学习在数据和计算时间方面可能代价很大;在最坏的情况下,它可能与解决整个任务一样昂贵。
我们提出了另一种观点,它模糊了发现option问题和学习option问题之间的界限。基于policy gradient 定理(Sutton等人。2000年),我们得到了一些新的结果,这些结果使得 \(intra-option\) 政策和终止函数的逐步学习过程能够与对它们的策略同时进行。在离散或连续的状态空间和动作空间下,这种方法可以自然地处理线性和非线性函数逼近器。当从单个任务中学习时,现有的学习option方法要慢得多:在类似的任务中重复使用已学习的选项,这是很大的好处。相比之下,我们证明了我们的方法能够在单个任务中成功地学习选项,而不会导致任何减速,同时仍然为转移学习提供好处。
- 我们首先回顾与我们工作的两个主要组成部分相关的背景:policy gradient method 和 option。
- 然后我们描述了我们方法的核心思想:the intra-option policy 和 termination gradient theorems。附加技术细节见附录。
- 实验结果表明,我们的方法能够有效地学习有意义的时间扩展行为。与其他方法不同,我们只需要指定所需选项的数量;不需要有子目标、额外奖励、描述demonstrations、多重问题或任何其他特殊调整(但是,如果需要,该方法可以利用伪奖励函数)。据我们所知,这是第一个端到端的学习方法,可以以相当的效率扩展到非常大的领域。
Preliminaries and Notation
一个马尔可夫决策过程包括:
为了方便起见,我们发展了假设离散状态和作用集的思想。然而,我们的结果扩展到连续空间使用通常的测量理论假设(我们的一些经验结果是在连续任务)。A (Markov Stationary) \(policy\) 是以状态为条件在动作上的概率分布:$$\pi:\mathcal{S}\times\mathcal{A}\to[0,1]$$。
在discount probelem中,策略\(\pi\)的值函数定义为期望:
其动作值函数为:
其中\(\gamma\in[0,1)\),为折扣因子。
一个策略 \(\pi\) 对给定的动作值函数 \(Q\) 是贪婪的,如果\(\pi(s,a)>0\)当且仅当\(a=\mathop{\arg\min}_{a'}Q(s,a')\)
在离散MDP中,至少有一个最优策略对其自身的作用值函数是贪婪的。
Policy gradient methods
policy gradient 方法(Sutton等人。2000;Konda和Tsitsiklis 2000)通过执行随机梯度下降来优化给定参数化随机策略族 \(\pi_\theta\) 的性能目标,来解决寻找一个好策略的问题。policy gradient 定理(Sutton等人。2000)提供了平均奖励和折扣奖励目标相对于θ的梯度的表达式。
在discounted 的设置下,目标是根据指定的开始状态(或分布)来定义的:
Policy gradient 定理表明:
\(\mu_{\pi\theta}(s|s_0)\) 是从 \(s_0\) 开始沿轨道的状态的折扣权重。
在实际应用中,政策梯度是沿着 on-policy 上的平稳分布从样本中估计出来的。(Thomas 2014)表明,忽略此平稳分布中的折扣因子会使通常的政策梯度估计有偏差。然而,纠正这种差异也会降低数据效率。为了简单起见,我们建立在(Sutton et al并根据(Thomas 2014)讨论如何扩展我们的结果。
The options framework
The options framework(Sutton、Precup和Singh 1999;Precup 2000)将时间扩展行动的概念正式化。
我们同时假设所有的options在任何地方都可以使用,即 \(\forall s\in\mathcal{S},\forall \omega\in\Omega:s\in\mathcal{I}_\omega\) ,这是大多数option发现算法中的一种假设。我们将在最后一节讨论如何消除这种假设。(Sutton,Precup,and Singh 1999;Precup 2000)表明,赋予一组option的MDP成为一个半马尔可夫决策过程(Puterman 1994,第11章),它在 \(V_\Omega(s)\) 和 option-value function \(Q_\Omega(s,\omega)\) 上具有对应的最优值函数。mdp的学习和规划算法在这种情况下有对应的算法。然而,底层MDP的存在提供了并行学习许多不同选项的可能性:这就是 \(intra\text{-}option\ learning\) 的思想,我们在工作中利用了这种思想。
Learning Options
我们对学习选择问题采取了持续的观点。在任何时候,我们都希望将所有可用的经验提炼到我们系统的每个组成部分:value function, policy over options, intra-option policies and termination functions 价值函数和期权政策、期权内政策和终止函数。为了实现这一目标,我们重点学习期权策略和终止函数,假设它们是用可微参数化函数逼近器表示的。
differentiable parameterized function approximators 可微参数化函数逼近器:
有很多 differentiable function approximators,如:
- 线性模型(Linear combinations of features)
- 神经网路(Neural network)
- 决策树(Decision tree)
- 最近邻(Nearest neighbour)
- ...
我们考虑了 \(call-and-return\) 执行模型,在该模型中,agent根据其在 \(\pi_\Omega\) 的策略选择option \(\omega\) ,然后遵循其 \(intra-option\) policy \(\pi_\omega\)直到终止(由 \(\beta_\omega\) 决定),此时该过程重复进行。
设 \(\pi_{\omega,\theta}\) 表示由θ参数化的option ω的intra-option policy,\(\beta_{\omega,\vartheta}\) 是由ϑ参数化的ω的终止函数。我们提出了两个新的学习option的结果,得到了作为蓝图的政策梯度定理(萨顿等人。2000年)。这两个结果都是在假设目标是学习使当前任务的预期收益最大化的option的前提下得出的。然而,如果要在目标函数中添加额外的信息,只要它以加性可微函数的形式出现,就可以很容易地做到这一点功能。
additive differentiable function:
假设我们的目标是优化在所有从指定状态 \(s_0\) 和option \(\omega_0\) 的轨迹上期望的discounted return,然后
7.24:此公式相对于式(a-1)同为 \(\rho()\) ,应该同样理解为\(s_0\) 的分布
请注意,此return取决于policy over options,以及option policies和termination函数的参数。我们将取这个目标相对于θ和ϑ的梯度。为了做到这一点,我们将使用类似于 \(intra-option\) 学习中使用的方程(Sutton,Precup,and Singh 1999,第8节)。具体来说,option-value 函数的定义可以写成:
首先可以很直观地看出此方法不是将option视为不可观察的黑盒,而是可以观察其内部更基础的action。基于此上式便可以理解为,option-value function就是基于状态s,option内策略得到值的期望,所以 \(Q_U()\) 从这个表达式推断,就可以推测是用来描述option内的state-action值函数,相当于是option的qlearning过程的值函数
\(Q_U:\mathcal{S}\times\Omega\times\mathcal{A}\to\mathbb{R}\) 是在state-option对的环境中执行action的值:
通过文章内的描述可以得知之前的推断是正确的,但是完全理解为option内的q-learning还是不妥
注意,\((s,ω)\)对导致了一个扩大的状态空间,参见(Levy和Shimkin 2011)。但是,我们不会显式地处理这个空间;它只用于简化推导。函数\(U:\Omega\times\mathcal{S}\to\mathbb{R}\)称为到达时的option-value函数(Sutton、Precup和Singh 1999,方程20)。
进入状态 \(s'\) 时执行 \(ω\) 的值由下式给出:
Between MDPs and semi-MDP中的表达式为:\(U(s,o)=(1-\beta(s))Q(s,o)+\beta(s)\mathop{\max}_{o'\in\mathcal{O'}}Q(s,o')\)
\(U(\omega,s')\) 的含义也即高亮——进入状态 \(s'\) 时执行 \(\omega\) 的值
\(P(s'|s,a)\) 指(s,a)时s'的概率,所以\(\sum_{s'}P(s'|s,a)U(\omega,s')\)即 \(\mathbb{E}[\omega|s,a]\)
请注意, \(Q_U\) and \(U\) 都依赖于θ和ϑ,但为了清楚起见,我们不在符号中包含它们。导出策略梯度所需的最后一个要素是Markov链,沿着该链可以估计性能度量。自然的方法是考虑在增广状态空间中定义的链,因为state-option对现在在通常的Markov链中扮演regular state的角色。如果option \(\omega_t\) 已经启动或在状态st的时间t执行,则一步中转换到 \((s_{t+1},ω_{t+1})\) 的概率为:
显然,(4)给出的过程是均匀的。在温和的条件下,且期权无处不在,它实际上是遍历的,并且在state-option对上存在唯一的稳态分布(stationary distribution)。
\(\mathbb{1}_{\omega_t=\omega_{t+1}}\) 的含义:简单理解应为 \(\omega_t=\omega_{t+1}\) 为1,不等则为0
所以对(4)的理解应为:*我将原文中的一处()改为了[]更有助于观察
整个的one-step概率公式为: intra-option策略在\(s_t\)时选择\(a\)的概率 乘以 \((s_t,a)\to s_{t+1}\)的转移概率 乘以 option变化的概率 之和
其中option变化的概率包括两部分:当 \(\omega_t\neq\omega_{t+1}\) 时,,即**option在\(s_{t+1}\) 时终止 并由上层策略 \(\pi_\Omega\) 选择了 \(\omega_{t+1}\) **;当 \(\omega_t=\omega_{t+1}\) 时,即 在 \(s_{t+1}\) 不终止仍为 \(\omega_t\) 的概率
稳态分布:
假设intra-option policies的参数 \(\theta\) 是随机可微的,我们现在将计算expected discounted return的梯度。从式(1,2)可以得到:
这一步的推导非常简单,就是直接展开
\[\because Q_\Omega(s,\omega)=\sum_a\pi_{\omega,\theta}(a|s)Q_U(s,\omega,a)\\ \therefore \frac{\partial Q_\Omega(s,\omega)}{\partial\theta}=\sum_a\left(\frac{\partial\pi_{\omega,\theta}(a|s)}{\partial\theta}Q_U(s,\omega,a)+\pi_{\omega,\theta}(a|s)\frac{\partial Q_U(s,\omega,a)}{\partial\theta}\right)\\ \because Q_U(s,\omega,a)=r(s,a)+\gamma\sum_{s'}P(s'|s,a)U(\omega,s')\\ \therefore \frac{\partial Q_U(s,\omega,a)}{\partial \theta}=\gamma\sum_{s'}P(s'|s,a)\frac{\partial U(\omega,s')}{\partial\theta} \]\[\frac{\partial Q_\Omega(s,\omega)}{\partial\theta}=\sum_a\frac{\partial\pi_{\omega,\theta}(a|s)}{\partial\theta}Q_U(s,\omega,a) + \sum_a\pi_{\omega,\theta}(a|s)\sum_{s'}\gamma P(s'|s,a)\frac{\partial U(\omega,s')}{\partial\theta}\tag{6} \]
我们可以用(3)和(4)进一步展开右手边,得到以下定理:
Intra-Option Policy Gradient Theorem
**Theorem 1 (Intra-Option Policy Gradient Theorem). **
给定一组参数 \(\theta\) 可微的随机intra-option的Markov期权,其gradient of the expected discounted return相对于 \(\theta\) 和初始条件 \((s_0,\omega_0)\) 的梯度为:
其中\(\mu_\Omega(s,\omega|s_0,\omega_0)\) 是state-option对沿着从 \((s_0,\omega_0)\) 开始的轨迹的discounted weighting,
证明在附录中。
为了阅读的连贯性将推导过程放在这里
在上述过程推导得到:
\[\frac{\partial Q_\Omega(s,\omega)}{\partial\theta}=\sum_a\frac{\partial\pi_{\omega,\theta}(a|s)}{\partial\theta}Q_U(s,\omega,a)+ \sum_a\pi_{\omega,\theta}(a|s)\sum_{s'}\gamma P(s'|s,a)\frac{\partial U(\omega,s')}{\partial\theta}\tag{6} \]\[\because U(\omega,s')=(1-\beta_{\omega,\vartheta}(s'))Q_\Omega(s',\omega)+\beta_{\omega,\vartheta}(s')V_\Omega(s')\tag{3} \]需要注意 \(\beta_{\omega,\vartheta}\) 定义即由 \(\vartheta\) 参数化的 \(\omega\) 的的终止函数,所以其中不含 \(\theta\)
\[\begin {aligned} \therefore \frac{\partial U(\omega,s')}{\partial \theta} &= (1-\beta_{\omega,\vartheta}(s'))\frac{\partial Q_\Omega(s',\omega)}{\partial \theta}+\beta_{\omega,\vartheta}(s')\frac{\partial V_\Omega(s')}{\partial \theta}\\ &=(1-\beta_{\omega,\vartheta}(s'))\frac{\partial Q_\Omega(s',\omega)}{\partial \theta}+\beta_{\omega,\vartheta}(s')\sum_{\omega'}\pi_\Omega(\omega'|s')\frac{\partial Q_\Omega(s',\omega')}{\partial \theta}\\ &=\frac{\partial Q_\Omega(s',\omega')}{\partial \theta}\sum_{\omega'}(\beta_{\omega,\vartheta}(s')\pi_\Omega(\omega'|s')+(1-\beta_{\omega,\vartheta}(s'))\mathbb{1}_{\omega=\omega'}) \end {aligned}\tag{7} \]将(7)带入(6)得:
\[\frac{\partial Q_\Omega(s,\omega)}{\partial\theta}=\sum_a\frac{\partial\pi_{\omega,\theta}(a|s)}{\partial\theta}Q_U(s,\omega,a) + \sum_a\pi_{\omega,\theta}(a|s)\sum_{s'}\gamma P(s'|s,a)\sum_{\omega'}(\beta_{\omega,\vartheta}(s')\pi_\Omega(\omega'|s')+(1-\beta_{\omega,\vartheta}(s'))\mathbb{1}_{\omega'=\omega})\frac{\partial Q_\Omega(s',\omega')}{\partial \theta}\tag{8} \]同时再引入上文已经提到得式(4),对其引入discount可得:
\[P^{(1)}_\gamma(s_{t+1},\omega_{t+1}|s_t,\omega_t)=\sum_a\pi_{\omega_t}(a|s_t)\gamma P(s_{t+1}|s_t,a)[(1-\beta_{\omega_t}(s_{t+1}))\mathbb{1}_{\omega_t=\omega_{t+1}}+\beta_{\omega_t}(s_{t+1})\pi_\Omega(w_{t+1}|s_{t+1})] \]同理可以得到同样的one-step转移概率:
\[P^{(1)}_\gamma(s_{t+1},\omega_{t}|s_t,\omega_{t-1})=\sum_a\pi_{\omega_t}(a|s_t)\gamma P(s_{t+1}|s_t,a)[(1-\beta_{\omega_{t-1}}(s_{t}))\mathbb{1}_{\omega_t=\omega_{t-1}}+\beta_{\omega_{t-1}}(s_{t})\pi_\Omega(w_{t}|s_{t})] \]进而可以得到k-steps的递归表达式:
\[P^{(k)}_\gamma(s_{t+k},\omega_{t+k}|s_t,\omega_t)=\sum_{s_{t+1}}\sum_{\omega_{t+1}}(P^{(1)}_\gamma(s_{t+1},\omega_{t+1}|s_t,\omega_t)P^{(k-1)}_\gamma(s_{t+k},\omega_{t+k}|s_{t+1},\omega_{t+1})) \]\[P^{(k)}_\gamma(s_{t+k},\omega_{t+k-1}|s_t,\omega_{t-1})=\sum_{s_{t+1}}\sum_{\omega_{t}}(P^{(1)}_\gamma(s_{t+1},\omega_{t}|s_t,\omega_{t-1})P^{(k-1)}_\gamma(s_{t+k},\omega_{t+k-1}|s_{t+1},\omega_{t})) \]所以针对式(8)论文给出化简:
\[\begin {aligned} \frac{\partial Q_\Omega(s,\omega)}{\partial\theta}&=\sum_a\frac{\partial\pi_{\omega,\theta}(a|s)}{\partial\theta}Q_U(s,\omega,a) + \sum_a\pi_{\omega,\theta}(a|s)\sum_{s'}\gamma P(s'|s,a)\sum_{\omega'}(\beta_{\omega,\vartheta}(s')\pi_\Omega(\omega'|s')+(1-\beta_{\omega,\vartheta}(s'))\mathbb{1}_{\omega'=\omega})\frac{\partial Q_\Omega(s',\omega')}{\partial \theta}\\ &=\sum_a\frac{\partial\pi_{\omega,\theta}(a|s)}{\partial\theta}Q_U(s,\omega,a) + \sum_{s'}\sum_{\omega'}P^{(1)}_\gamma(s',\omega'|s,\omega)\frac{\partial Q_\Omega(s',\omega')}{\partial \theta}\\ &=\sum_{k=0}^\infty\sum_{s',\omega'}P^{(k)}_\gamma(s',\omega'|s,\omega)\sum_a\frac{\partial\pi_{\omega',\theta}(a|s')}{\partial\theta}Q_U(s',\omega',a)\\ \end{aligned}\tag{9} \]疑问:(9)中第二步是如何到第三步的
问题关键:要注意表达式中字母角标的变化,递归得到的该表达式
\[\frac{\partial Q_\Omega(s',\omega')}{\partial\theta}=\sum_a\frac{\partial\pi_{\omega',\theta}(a|s')}{\partial\theta}Q_U(s',\omega',a) + \sum_{s''}\sum_{\omega''}P^{(1)}_\gamma(s'',\omega''|s',\omega')\frac{\partial Q_\Omega(s'',\omega'')}{\partial \theta}\\ \]\[\begin {aligned} \frac{\partial Q_\Omega(s,\omega)}{\partial\theta} &=\sum_a\frac{\partial\pi_{\omega,\theta}(a|s)}{\partial\theta}Q_U(s,\omega,a) + \sum_{s'}\sum_{\omega'}P^{(1)}_\gamma(s',\omega'|s,\omega)\frac{\partial Q_\Omega(s',\omega')}{\partial \theta}\\ &=\sum_a\frac{\partial\pi_{\omega,\theta}(a|s)}{\partial\theta}Q_U(s,\omega,a) + \sum_{s'}\sum_{\omega'}P^{(1)}_\gamma(s',\omega'|s,\omega)\left(\sum_a\frac{\partial\pi_{\omega',\theta}(a|s')}{\partial\theta}Q_U(s',\omega',a) + \sum_{s''}\sum_{\omega''}P^{(1)}_\gamma(s'',\omega''|s',\omega')\frac{\partial Q_\Omega(s'',\omega'')}{\partial \theta}\right)\\ &=\dots\\ &=\sum_{k=0}^\infty\sum_{s',\omega'}P^{(k)}_\gamma(s',\omega'|s,\omega)\sum_a\frac{\partial\pi_{\omega',\theta}(a|s')}{\partial\theta}Q_U(s',\omega',a)\\ \end{aligned} \]
这个梯度描述了原始水平上局部变化对全局期望折现收益的影响。相反,sub-goal或pseudo-reward方法假设option的目标仅仅是优化其自身的奖励函数,而忽略了提议的变更如何在总目标中如何传播。
Termination Gradient Theorem
现在我们将注意力转向计算终止函数的梯度,这次假设是随机的,并且在ϑ中是可微的。
从(1,2,3)可以得到:
直接展开,很容易得到
因此,关键量是 \(U\) 的梯度。这是call-and-return执行的自然结果,其中终止函数的“goodness”只能在进入下一个状态时评估。相关梯度可进一步扩展为:
其中 \(A_\Omega\) 是advantage function(Baird,1993),\(A_\Omega(s',\omega)=Q_\Omega(s',\omega)-V_\Omega(s')\)。
递归地展开 \(\frac{\partial U(\omega',s'')}{\partial\vartheta}\) 得到了与定理(1)相似的形式,但其中状态-选项对的权重现在是根据移动一个时间步的马尔可夫链:\(\mu_\Omega(s_{t+1},\omega_t|s_t,\omega_{t+1})\)(详见附录)。
Theorem 2 (Termination Gradient Theorem).
给出一组随机终止函数在其参数ϑ上可微的Markov期权,期望折现收益目标相对于ϑ和初始条件(s1,ω0)的梯度为:
其中\(\mu_\omega(s',\omega|s_1,\omega_0)\) (s1,ω0)中状态选项对的贴现权重:
优势函数经常出现在政策梯度方法中(Sutton等人。2000年)在形成基线以减少梯度估计的方差时。它在这种情况下的出现主要与算法设计有关。有趣的是,在我们的例子中,它是推导的直接结果,并且给了定理一个直观的解释:当期权选择相对于所有期权的期望值是次优时,优势函数是负的,它推动梯度修正上升,这增加了终止的几率。终止后,代理有机会使用πΩ选择更好的选项。类似的想法也构成了期权的中断执行模型(Sutton,Precup,and Singh 1999),在该模型中,只要QΩ(s?,ω)对于电流选项ω小于VΩ(s?)。(Mann、Mankowitz和Mannor 2014)最近在数值迭代设置下,通过打断Bellman算子的镜头研究了中断选项。终止梯度定理可以解释为提供了一个基于梯度的中断Bellman算子。
Algorithms and Architecture
基于定理1和定理2,我们现在可以设计一个学习option的随机梯度下降算法。利用双时间尺度框架(Konda和Tsitsiklis 2000),我们建议在快速的时间尺度上学习value,同时以较慢的速度更新内部期权策略和终止函数。
two-timescale framework:
我们将产生的系统称为一个 \(option\text{-}critic\ architecture\) ,参考actor-critic架构(Sutton 1984)。option内策略、终止函数和option上的策略属于系统的actor部分,而critic则由 \(Q_U\) 和 \(A_\Omega\) 组成。option-critic体系结构没有规定如何获得 \(\pi_\Omega\) ,因为现有的各种方法都可以应用:在SMDP级别使用策略梯度方法,在option模型上使用规划器,或者使用时间差分更新。如果 \(\pi_\Omega\) 是option上的贪婪策略,则由(2)得到相应的一步策略更新目标 \(g_t^{(1)}\) :
这也是Sutton,Precup和Singh 1999的intra-option Q-learning算法的更新目标。算法1给出了一个使用option内Q学习的option critic的原型实现。假设的表格设置只是为了表达的清晰。我们分别给出了critic、intra-option策略和终止函数的学习率的 \(\alpha,\alpha_\theta,\alpha_\vartheta\)。
\(Q_U:(2)\)
除 \(Q_\Omega\) 学习 \(Q_U\) 在计算上浪费了大量的参数和样本。一个实际的解决方案是只学习 \(Q_\Omega\) 并从中得到 \(Q_U\) 的估计值。因为 \(Q_U\) 是对下一个state的期望, \(Q_U(s,\omega,a)=\mathbb{E}_{s'\sim P}[r(s,a)+\gamma U(\omega,s')|s,\omega,a]\) ,结果表明 \(g_t^{(1)}\) 是一个合适的估计量。我们选择这种方法作为我们在Arcade Learning Environment中使用深度神经网络的实验。
Experiments
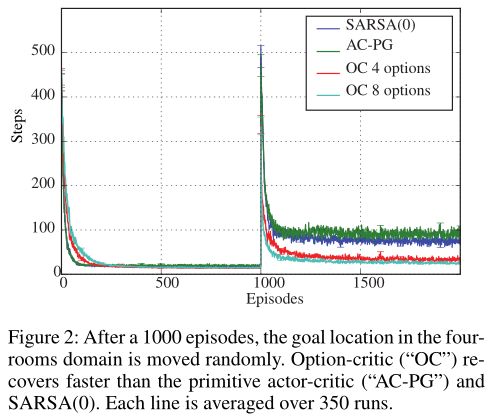
我们首先考虑四个房间域中的导航任务(Sutton、Precup和Singh 1999)。我们的目标是评估一组完全自主学习的option从环境的突然变化中恢复过来的能力。(Sutton,Precup,and Singh 1999)对一组预先指定的选项提出了一个类似的实验;我们的结果中的选项并不是事先指定的。
最初目标位于 east doorway (\(G1\)),初始状态从所有其他单元统一绘制。 1000episode之后,目标移动到右下角房间的一个随机位置。
原始移动可能以1/3的概率失败,在这种情况下,代理会随机过渡到一个空的相邻单元。折扣系数为0.99,进球时奖励为+1,否则奖励为0。
与(Sutton,1999)设置相同,另\(\gamma=0.99\)
我们选择用Boltzmann分布参数化intra-option策略,用sigmoid函数参数化终止策略。
使用intra-optionQ学习方法学习了options上的策略(high level)。
我们还使用Boltzmann策略实现了原始的actor-critic(表示为AC-PG)。
我们还比较了option-critic和使用Boltzmann exploration和没有eligibility trace的原始的SARSA agent。对于所有的Boltzmann策略,我们将温度参数设置为0.001。所有的权重都被初始化为零。
Boltzmann分布:
Boltzmann策略:
temperature parameter:
如图2所示,当目标突然改变时,Option-Critic agent恢复得更快。此外,初始的选项集是从零开始学习的速度可与原始方法相媲美。尽管这个领域很简单,但我们还没有发现其他方法可以在不产生比单独使用原始操作时更大的成本的情况下解决这个任务(McGovern和Barto 2001;S¸ims¸ek和Barto 2009)。
在有4个option和8个option的两个临时扩展设置中,终止事件更可能发生在门口附近(图3),这与直觉一致,即它们是好的子目标。与(Sutton,Precup,and Singh 1999)相反,我们自己并没有对这些知识进行编码,而是让agent找到能够最大化expected discounted return的option。
Pinball Domain
在弹球领域(Konidaris and Barto 2009),球必须通过一个任意形状的多边形迷宫引导到指定的目标位置。状态空间在xy平面上球的位置和速度是连续的。在每一步,代理必须在五个离散的基本动作中进行选择:更快或更慢地移动球,在垂直或水平方向上,或采取null action。与障碍物的碰撞是弹性的,可以利用agent的优势。在这个环境中,当重复选择不动作时,0.995的阻力系数有效地阻止了球在有限步数后的运动。每一个动作都会受到−5的惩罚,而不采取任何行动的代价是−1。当agent到达目标时,该事件将以+10000奖励结束。我们中断了超过10000episode的任何episode,并将折扣系数设置为0.99。
我们在critic中使用了intra-option的Q-学习,在 order 3 的 Fourier base上使用线性函数逼近(Konidaris et al.2011)。
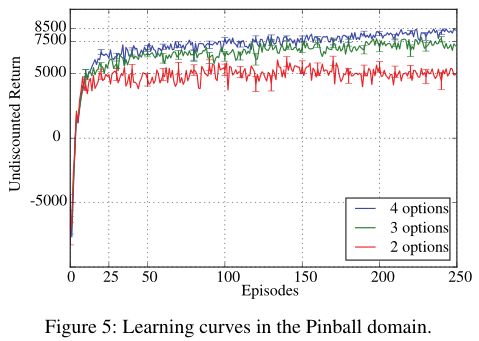
我们尝试了2,3或4个option。我们使用Boltzmann策略作为intra-option策略,线性sigmoid函数用于终止函数。critic的学习率设为0.01,内部和终止梯度的学习率设为0.001。我们在期权上使用了epsilon-greedy政策,\(\epsilon=0.01\)。
在(Konidaris and Barto 2009)中,只有在gestation为10期后才可以使用和更新option。由于学习是完全整合在选项评论家,到40集,一个近乎最佳的option集合已经学习在所有的设置。从定性的角度来看,这些option表现出时间上的扩展和专门化(图4)。我们还观察到,在许多成功的轨迹中,红色option将始终用于目标附近。
Arcade Learning Environment
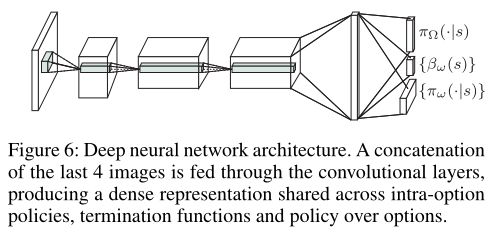
我们在Arcade Learning Enviroment(ALE)(Bellemare等人。2013年)使用深度神经网络来近似临界值(critic)并表示内部期权政策和终止函数。我们使用了与(Mnih等人。2013年)网络相同的前3个卷积层。我们在第一层使用32个8×8和4个步长的卷积滤波器,在第二层使用64个4×4的步长为2的滤波器,在第三层使用64个步长为1的3×3滤波器。然后,我们将第三层的输出输入到由512个神经元组成的dense shared layer中,如图6所示。我们将期权内策略和终止梯度的学习率固定为0.00025,并使用RMSProp作为批评函数。
我们将期权内策略表示为第四层(稠密)的线性softmax,以输出基于当前观察的操作的概率分布。终止函数的定义类似于使用sigmoid函数,每个终端有一个输出神经元。
使用带经验回放的option内学习训练critic网络。期权政策和终止被在线更新。我们用的是\(\epsilon\)-greedy的optiion政策 \(\epsilon\)=0.05试验阶段(Mnih等人。2013年)。
(未完)
Related Work
由于期权发现最近受到广泛关注,我们现在更详细地讨论我们的方法相对于其他方法的地位。(Comanici和Precup 2010)使用基于梯度的方法,仅改进半马尔可夫期权的终止函数;终止通过自启动以来观察到的特征的累积测量值的逻辑分布建模。(Levy和Shimkin 2011)也建立在政策梯度方法上,通过明确地构造增广的状态空间,并将停止事件视为额外的控制动作。相反,我们不需要直接构建这个(非常大)空间。(Silver and Ciosek 2012)通过依赖组合特性将期权动态链接到更长的时间序列中。早期关于线性期权的研究(Sorg和Singh,2010年)也使用组合性来规划使用线性预期模型的期权。我们的方法也依赖于Bellman方程和组合性,但与策略梯度方法相结合。
最近几篇论文还试图将期权发现描述为一个优化问题,其解与函数逼近相容。(丹尼尔等人。2016)通过将终止函数作为隐变量来学习收益优化选项,并使用EM学习它们。(V ezhnevets等人。2016)考虑具有开环期权内策略的学习期权问题,也称为宏观行动。与经典规划一样,缓存更频繁的动作序列。一个从状态到动作序列的映射,以及一个承诺模块,在必要时触发重新规划。相反,我们始终使用闭环策略,这些策略对状态信息是反应性的,可以提供更好的解决方案。(Mankowitz,Mann,and Mannor 2016)提出了一种基于梯度的选项学习算法,假设起始集和终止函数具有特定的结构。在这个框架下,在状态空间的任何分区中只有一个选项是活动的。
(Kulkarni et al. 2016)利用DQN框架实现了一个基于梯度的期权学习器,它利用内在的奖励来学习期权的内部政策,而外部的奖励来学习期权的政策。与我们的框架不同,子目标的描述是作为选项学习者的输入。期权批评家在概念上是一般的,不需要内在动机来学习期权。
Discussion
我们开发了一种通用的基于梯度的方法来同时学习期权内策略和终止函数,以及策略优先于期权,以优化当前任务的性能目标。我们的ALE实验证明了在非线性函数逼近下,期权的端到端学习是成功的。如前所述,我们的方法只需要指定选项的数量。然而,如果想要使用额外的伪奖励,option-critic框架将很容易地适应它。在这种情况下,内部策略和终止函数梯度只需考虑伪奖励而不是任务奖励。这个想法的一个简单例子,我们在一些实验中使用了,就是使用额外的奖励来鼓励那些确实在时间上被延长的选项,只要一个转换事件发生就增加一个惩罚。我们的方法可以与任何其他启发式方法无缝地合作,使选项集偏向于某些期望的属性(例如,组合性或稀疏性),只要它可以表示为一个附加的奖励结构。然而,从结果中可以看出,这样的偏差并不是产生良好结果的必要条件。
期权批评家体系结构依赖于策略梯度定理,正如(Thomas 2014)中所讨论的,梯度估计在折扣情况下可能是有偏的。通过引入γt?t i=1(1−βi)在我们的更新(Thomas 2014,公式(3))中,可以获得无偏估计值。然而,我们不推荐这种方法,因为无偏估计量的样本复杂度通常过高,且有偏估计量在我们的实验中表现良好。
也许我们工作的最大的局限性是假设所有的选择都适用于任何地方。在函数逼近的情况下,初始集的一个自然扩展是在特征上使用分类器,或其他形式的函数逼近。因此,确定允许哪些选项可能与评估策略优于选项的成本类似(与表格设置不同,在表格设置中,具有稀疏初始集的选项会导致更快的决策)。这类似于合格跟踪,后者比在表格情况下不使用跟踪更昂贵,但与函数近似具有相同的复杂性。如果要学习初始集,则需要添加的主要约束条件是,在增广状态选项空间中,选项及其上的策略会导致遍历链。这可以表示为连接起始集和终止集的流条件。这个条件的精确描述,以及初始集的稀疏正则化,留待以后的工作。