Kaggle Getting Started房价预测竞赛

没怎么做过kaggle的题目，对机器学习的套路还不是非常熟悉，然后前段时间碰到了一个回归的问题，竟然不知道如何下手，Kaggle上有一个房价预测的基础回归问题，机器学习回归就从这里开始好了。
学习资料：https://www.kaggle.com/marsggbo/kaggle
\quad 完整的机器学习算法解决房价预测需要处理以下几个问题：
1、 理解问题：观察每个变量特征的意义以及对于问题的重要度
2、 理解主要特征：也就是最终的目的变量—房价
3、 基础的数据清洗：对一些缺失的，异常点和分类数据进行处理
4、 测试假设
我也将按照这个步骤来解决这个问题

数据导入

#导入需要的模块
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np

#用来绘图的，封装了matplot
#一旦导入了seaborn,matplotlib的作图风格会被覆盖为seaborn
import seaborn as sns
from scipy import stats
from scipy.stats import norm #生成正态分布的离散变量
from sklearn.preprocessing import StandardScaler #计算训练数据集的平均值和标准差,以便测试集使用相同的变换

#导入数据
data_train = pd.read_csv("/home/zxy/PycharmProjects/Kagglemarsggbo/data/train.csv")

# print(data_train)

观察特征变量和房价售价的关系

1. 分析"SalePrice"

print(data_train['SalePrice'].describe())

输出为：

count      1460.000000
mean     180921.195890
std       79442.502883
min       34900.000000
25%      129975.000000
50%      163000.000000
75%      214000.000000
max      755000.000000
Name: SalePrice, dtype: float64

可以看出，SalePrice变量没有无效和非数值的数据，然后作者还提供了一种图示化方法来展示salePrice

sns.distplot(data_train['SalePrice'])
plt.show()

可以看出房价是呈现正态分布的。同时作者还介绍了2个统计学的概念：峰度(Kurtosis)和偏度(Skewness)，其中峰度是描述某变量所有取值分布形态抖缓程度的统计量。它是和正太分布相比较的。
峰度

1. Kurtosis = 0 与正态分布的抖缓程度相同
2. Kurtosis > 0 比正态分布的高峰更加陡峭 — 尖顶峰
3. Kurtosis > 0 比正太分布的高峰来的平 — 平顶峰
4. 计算公式：

• 峰度为0表示该总体数据分布与正态分布的陡缓程度相同。
• 峰度 >0表示该总体数据分布与正态分布相比较为陡峭，为尖顶峰。
• 峰度 <0表示该总体数据分布与正态分布相比较为平坦，为平顶峰。
  峰度的绝对值数值越大表示其分布形态的陡缓程度与正态分布的差异程度越大。

偏度
6. Skewness = 0 分布形态与正太分布偏度相同
7. Skewness > 0 正偏差数值较大，为正偏或右偏。长尾巴拖在左边。
8. Skewness < 0 负偏差数值较大，为负偏或左偏。长尾巴拖在左边。
9. 计算公式：

• 偏度为0表示其数据分布形态与正态分布的偏斜程度相同。
• 偏度 >0表示其数据分布形态与正态分布相比为正偏或右偏，即有一条长尾巴拖在右边，数据右端有较多的极端值，数据均值右侧的离散程度强。
• 偏度 <0表示其数据分布形态与正态分布相比为负偏或左偏，即有一条长尾拖在左边，数据左端有较多的极端值，数据均值左侧的离散程度强。

打印出这两个值：

print("Skewness: %f" % data_train['SalePrice'].skew())
print("Kurtosis %f" % data_train['SalePrice'].kurt())

结合上面的图形容易看出，长尾巴确实拖在右边，而且高峰陡峭。

2. 验证特征是否满足需求

类别特征

1. CentralkAir中央空调

#CentralAir
var = 'CentralAir'
data = pd.concat([data_train['SalePrice'], data_train[var]], axis=1)
fig = sns.boxplot(x = var, y = 'SalePrice', data=data)
fig.axis(ymin=0, ymax=800000);
plt.show()

可以看出有中央空调的房价明显更高。

2. OverallQual总体评价

# OverallQual 总体评价
var = 'OverallQual'
data = pd.concat([data_train['SalePrice'], data_train[var]], axis=1)
fig = sns.boxplot(x = var, y = 'SalePrice', data=data)
fig.axis(ymin=0, ymax=800000)
plt.show()

3.YearBuilt 建造年份

# OverallQual 总体评价
# var = 'OverallQual'
# data = pd.concat([data_train['SalePrice'], data_train[var]], axis=1)
# fig = sns.boxplot(x = var, y = 'SalePrice', data=data)
# fig.axis(ymin=0, ymax=800000)
# plt.show()

#YearBuilt boxplot
var = 'YearBuilt'
data = pd.concat([data_train['SalePrice'], data_train[var]], axis=1)
data.plot.scatter(x=var, y="SalePrice", ylim=(0, 800000))
plt.show()

第一个箱线图看得不是很明显，所以用点图来表示，

可以看出，建造年份越晚，价格越高。

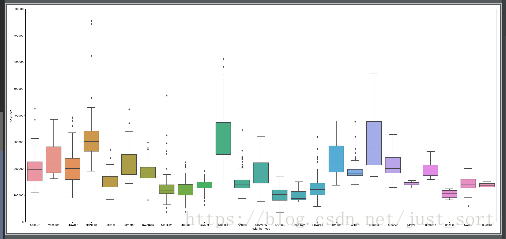
4. Neighborhood地段

#Neighborhood
var = 'Neighborhood'
data = pd.concat([data_train['SalePrice'], data_train[var]], axis=1)
f, ax = plt.subplots(figsize=(26,12))
fig = sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, ymax=800000)
plt.show()

Neighborhood地段

数值型特征

1. LotArea地表面积

#LotArea 地表面积
var = 'LotArea'
data = pd.concat([data_train['SalePrice'], data_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000))
plt.show()

这个特征对房价的影响不大，所以不考虑

2. GrliveArea 生活面积

#GrliveArea 生活面积
var = 'GrLivArea'
data = pd.concat([data_train['SalePrice'], data_train[var]], axis=1)
data.plot.scatter(x = var, y = 'SalePrice', ylim=(0,800000))
plt.show()

可以看出生活面积对房价的影响比较大。

3.TotalBsmtSF 地下室总面积

#TotalBsmSF地下室总面积
var = 'TotalBsmtSF'
data = pd.concat([data_train['SalePrice'], data_train[var]], axis=1)
data.plot.scatter(x = var, y = 'SalePrice', ylim=(0, 800000))
plt.show()

可以看出这个变量和房价呈现线性关系，所以也是可以考虑的。

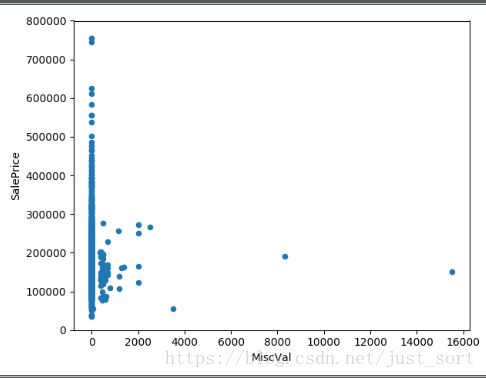
4. MiscVal 附加值

#MiscVal 附加值
var = 'MiscVal'
data = pd.concat([data_train['SalePrice'], data_train[var]], axis=1)
data.plot.scatter(x = var, y='SalePrice', ylim=(0, 800000))
plt.show()

可以看出附加值这个变量和房价没有关系，所以可以不考虑

5. GarageArea/GarageCars 车库

# GarageArea/GarageCars 车库
var = ['GarageArea', 'GarageCars']
for index in range(2):
    data = pd.concat([data_train['SalePrice'], data_train[var[index]]], axis=1)
    data.plot.scatter(x=var[index], y='SalePrice', ylim=(0, 800000))
plt.show()

从上面的图看出房价与车库面试和容量车辆数呈现线性关系，所以入选主特征。

3. 更加科学的分析依据

3.1 关系矩阵

\quad 上面对特征变量的分析是比较模糊的，为了让我们更好的评估我们的变量是否对结果有用需要做到以下几点：

1. 得到各个特征之间的关系矩阵
2. 'SalePrice’的关系矩阵
3. 绘制出最相关的特征之间的关系图

代码如下：

corrmat = data_train.corr() #相关系数矩阵
f, ax = plt.subplots(figsize=(20, 9))
sns.heatmap(corrmat, vmax=0.8, square=True)
plt.show()

从这个图我们可以直接看到，像素块越红表示相关性越大，所以我们可以看到与"SalePrice"相关性很强的有：

1. OverallQual 总体评价
2. YearBuilt 建造年份
3. TotalBsmSF：地下室面积
4. 1stFlrSF：一楼面积
5. GrLiveArea: 生活区面积
6. 'FullBath'：浴室
7. ToRmsAbvGrd:总房间数
8. GarageCars: 车库可容纳车辆数
9. GarageArea： 车库面积
   然后这个相关图里面有一些Trick，第一个是这些特征里面有一些特征是十分类似的，例如FGarageCars和GarageArea，TotaoBsmSF和1stFlrSF。第二个是上面出现的变量都是数值型的，像Neighborhood这种离散型数据没有参与到计算，下面会利用sklearn来对这些特征进行处理。

from sklearn import preprocessing
f_names = ['CentralAir', 'Neighborhood']
for x in f_names:
    label = preprocessing.LabelEncoder() #LabelEncoder就是对不连续的数字或者文本进行编号
    data_train[x] = label.fit_transform(data_train[x])
corrmat = data_train.corr()
f, ax = plt.subplots(figsize=(20, 9))
sns.heatmap(corrmat, vmax=0.8, square=True)
plt.show()

利用这个信息可以得到，CentralAir和Neighborhood这两个特征对房价的影响，所以后面将不予考虑。

3.2 房价关系矩阵

k = 10 #关系矩阵中将显示10个特征
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index
cm = np.corrcoef(data_train[cols].values.T) #相关系数,也可以看成协方差
sns.set(font_scale=1.25) #字体大小缩放比例？
# heatmap API:https://blog.csdn.net/cymy001/article/details/79576019
hm  = sns.heatmap(cm, cbar=True, annot=True,\
                  square=True, fmt='.2f', annot_kws={'size':10}, yticklabels=cols.values,\
                  xticklabels=cols.values)
labels = cols.values
plt.show()

分析得到我们需要考虑的特征值如下：GrLKivArea(生活面积),TotRmsAbvGrd(总房间数),FullBath(浴室数量),TotalBsmSF(地下室总面积),GarageCars(车库),YearBuilt(建造年份),QverallQual(总体评价)。

4. 数据模拟

#导入模型
from sklearn import preprocessing
from sklearn import linear_model, svm, gaussian_process
from sklearn.ensemble import RandomForestRegressor
from sklearn.cross_validation import train_test_split
import numpy as np

#导入数据
cols = ['OverallQual', 'GrLivArea', 'GarageCars', 'TotalBsmtSF', 'FullBath',
        'TotRmsAbvGrd', 'YearBuilt']
x = data_train[cols].values
y = data_train['SalePrice'].values
x_scaled = preprocessing.StandardScaler().fit_transform(x) #归一化数据
y_scaled = preprocessing.StandardScaler().fit_transform(y.reshape(-1, 1)) #归一化数据并且拉成一个列向量
X_train, X_test, y_train, y_test = train_test_split(x_scaled, y_scaled, test_size=0.33, random_state=42)

clfs = {
    'svm': svm.SVR(),
    'RandomForestRegressor':RandomForestRegressor(n_estimators=400),
    'BayesianRidge':linear_model.BayesianRidge()
}

for clf in clfs:
    try:
        clfs[clf].fit(X_train, y_train)
        y_pred = clfs[clf].predict(X_test)
        print(clf + " cost:" + str(np.sum(y_pred - y_test) / len(y_pred)))
    except Exception as e:
        print(clf + "Error:")
        print(str(e))

输出结果：

svm cost:-17.967306347608588
BayesianRidge cost:-17.19150469291163
RandomForestRegressor cost:-0.9689254868891797

可以看出随机深林的损失函数最小，所以采用随机深林对模型进行预测

5. 检验测试数据

import pandas as pd
from sklearn.ensemble import RandomForestRegressor
rfr = dst
data_test = pd.read_csv("/home/zxy/PycharmProjects/Kagglemarsggbo/data/test.csv")
print(data_test[cols].isnull().sum())

OverallQual     0
GrLivArea       0
GarageCars      1
TotalBsmtSF     1
FullBath        0
TotRmsAbvGrd    0
YearBuilt       0
dtype: int64

因为数据中存在缺失的值，所以不能直接predict，而且缺失值较少，所以直接用数据的均值来替代，所以接下来计算缺失值的均值即可。

cols2 = ['OverallQual', 'GrLivArea', 'FullBath', 'TotRmsAbvGrd', 'YearBuilt']
cars = data_test['GarageCars'].fillna(1.766118)
bsmt = data_test['TotalBsmtSF'].fillna(1046.117970)
data_test_x = pd.concat([data_test[cols2], cars, bsmt], axis=1)
print(data_test_x.isnull().sum())
x = data_test_x.values
y_ = rfr.predict(x)
print(y_)
print(y_.shape)
print(x.shape)

predictions = pd.DataFrame(y_, columns=['SalePrice'])
result = pd.concat([data_test['Id'], predictions], axis=1)

result.to_csv('./Predictions.csv', index=False)

至此，baseline就完成了，那么如何提高准确率呢？

提升准确率

机器学习模型之XGBoost参数记录

• eta 默认值为0.3，每次迭代完成后更新权重的步长，也就是学习率。
• min_child_weight 默认为1，代表最小叶子节点样本权重和，用于避免过拟合，当它的值较大时，可以避免模型学习到局部的特殊样本，但是如果这个值太高会导致欠拟合，需要使用CV来调整。
• max_depth默认值为6，为树的最大深度，max_depth越大，模型会学到更具体更局部的样本，需要用CV函数来微调，典型值3-10.
• max_leaf_nodes 树上最大的节点或叶子的数量，可以替代max_depth的作用，因为如果是二叉树，一个深度为n的树最多生成2^n个叶子。
• gamma 在节点分裂时，只有分裂后损失函数的值下降了，才会分裂这个节点。Gamma指定了分裂所需要的最小损失函数下降值，这个值越大算法越保守。这个参数的值和损失函数息息相关，所以是需要调整的。
• subsample. 控制对于每棵树随机采样的比例。减小这个参数的值，算法会更加保守，避免过拟合。但是如果这个参数的值设置得太小，会导致过拟合。典型值0.5-1
• colsample_bytree默认值为1，用来控制每棵随机采样的列数的占比。典型值0.5-1.0
• lambda默认值为1，权重的L2正则化，可以用于在很高维度下是的算法更快。
• alpha，默认值为1，权重的L1正则化。
• scale_pos_weight在各类样本十分不平衡时，把这个参数设置为一个正值，可以让算法更快的收敛。
• objective,默认为reg::linear，这个参数定需要被最小化的损失函数。最常用的值为:binary:logistic二分类的逻辑回归，返回预测的概率。multi:softmax使用softmax的多分类器，返回预测的类别，这时需要多设一个参数为num_class（类别数），multi:softprob和multi:softmax参数一样，但是返回是的每个数据属于各个类别的概率。
• eval_metric默认值取决于objective参数的取值。对于有效数据的度量方法，对于回归问题，默认值是rmse，对于分类问题默认值是error。典型值有rmse均方根误差$\sqrt{\frac{{\sum }_{i=1}^N{x}^2}{N}}$，mae平均绝对误差$\frac{{\sum }_{i=1}^N|x|}{N}$，logloss负对数似然函数值,error二分类错误率(阈值为0.5),merror多分类错误率,mlogloss多分类logloss损失函数,auc曲线包围面积。
• seed 默认值为0的随机种子，记录下以便于复现模型。

机器学习模型之SVR参数记录

• 核函数的类型：一般有’rbf’, ‘linear’, ‘poly’, ‘sigmoid’。
• C:惩罚因子。C表示有多么重视离群点，C越大越重视，越不想丢掉它们。C值越大时对误差分类的惩罚增大，C值小时对误差分类的惩罚减小。当C越大，趋近于无穷时，表示不允许分类误差的存在，margin越小，越容易过拟合；当C趋近于0时，表示我们不再关注分类是否正确，只要求margin越大，容易欠拟合。
• gamma 是’rbf’, ‘poly’, 'sigmoid’的核系数且gamma的值必须大于0.随着gamma的增大，存在对于测试集分类效果差而对训练分类效果好的情况，并且容易泛化误差出现过拟合。

##机器学习模型之Lasso参数记录

• alpha 它通过构造一个惩罚函数得到一个较为精炼的模型，使得它压缩一些系数，同时设定一些系数为零。因此保留了子集收缩的优点，是一种处理具有复共线性数据的有偏估计。
• max_iter 最大迭代次数

机器学习模型之Ridge参数记录

-alpha 惩罚系数

机器学习模型之Kernel Ridge Regression

• alpha: float或者list（当y是多目标矩阵时）
• kernel: 核函数的类型包括
  
• gamma：rbf，laplacian，poly，chi2，sigmoid核中的参数，使用其他核时无效
• degree：poly核中的参数d，使用其他核时无效
• coef0：poly和sigmoid核中的0参数的替代值，使用其他核时无效

机器学习模型之ElasticNet回归(弹性网回归)

• alpha 惩罚系数
• l1_ratio l1正则化惩罚比例

机器学习模型之贝叶斯线性回归模型

• 无参数