李宏毅学习笔记34.GAN.05.fGAN: General Framework of GAN

简介

上节在讲原文GAN的时候，提到我们实际是在用Discriminator来衡量两个数据的分布之间的JS divergence，那能不能是其他类型的divergence来衡量真实数据和生成数据之间的差距？又如何进行衡量？（虽然在实作上用不同divergence结果没有很大差别）
公式输入请参考：在线Latex公式

f-divergence

任意的divergence都可以用来衡量真实数据和生成数据之间的差距，用f-divergence进行衡量的算法就叫fGAN。先来看看f-divergence的概念：
$P$ and $Q$ are two distributions. $p(x)$ and $q(x)$ are the probability of sampling $x$.
$$D_f(P||Q)={\int }_{x}q(x)f\left(\frac{p(x)}{q(x)}\right)dx,\text{f is convex, }f(1)=0$$
如果两个分布相同，那么f-divergence的值应该相等，我们来验证一下：
当$p(x)=q(x)\text{ for all }x$
$$D_f(P||Q)={\int }_{x}q(x)f\left(\frac{p(x)}{q(x)}\right)dx=0$$
因为：$\frac{p(x)}{q(x)}=1,f(1)=0$，所以divergence为0，是最小的f-divergence。证明如下：
Because f is convex，因此有（右边是左边的lower bound）：
$$D_f(P||Q)={\int }_{x}q(x)f\left(\frac{p(x)}{q(x)}\right)dx\ge f\left({\int }_{x}q(x)\frac{p(x)}{q(x)}dx\right)$$
$$f\left({\int }_{x}q(x)\frac{p(x)}{q(x)}dx\right)=f\left({\int }_{x}p(x)dx\right)=f(1)=0$$
如果$f$是不同的函数，就得到不同的divergence，例如：$f(x)=xlogx$
$$\begin{gathered} D_f(P||Q)={\int }_{x}q(x)\frac{p(x)}{q(x)}log\left(\frac{p(x)}{q(x)}\right)dx \\ ={\int }_{x}p(x)log\left(\frac{p(x)}{q(x)}\right)dx \end{gathered}$$
这个是KL divergence。
例如：$f(x)=-logx$
$$\begin{gathered} D_f(P||Q)={\int }_{x}q(x)\left(-log\left(\frac{p(x)}{q(x)}\right)\right)dx \\ ={\int }_{x}q(x)log\left(\frac{q(x)}{p(x)}\right)dx \end{gathered}$$
这个是Reverse KL divergence。
例如：$f(x)=(x-1{)}^2$
$$\begin{gathered} D_f(P||Q)={\int }_{x}q(x){\left(\frac{p(x)}{q(x)}-1\right)}^{2}dx \\ ={\int }_x\frac{{\left(p(x)-q(x)\right)}^2}{q(x)}dx \end{gathered}$$
这个是Chi Square divergence。

Fenchel Conjugate

每一个$f$凸函数都有一个Conjugate函数记为$f^{\ast }$，公式如下：
$$f^{\ast }(t)=\underset{x\in dom(f)}{\max }\{xt-f(x)\}$$
穷举所有的$t,x$，然后找到能使得$xt-f(x)$最大的$t,x$。
比较笨的穷举法如下：

另外一种方法：函数$xt-f(x)$是直线，我们带不同的$x$得到不同的直线，例如下面有三条直线：

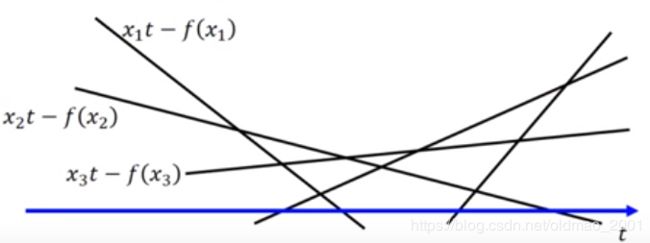
然后找不同的t对应的最大值。（就是所有直线的upper bound）

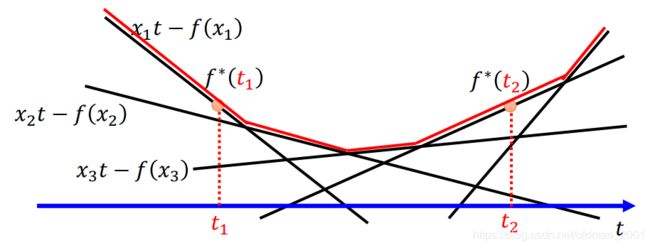
上面的红线无论你如何画，最后都是convex的。
看例子，假设：$f(x)=xlogx$，把$x=0.1,x=1,x=10$，图片如下：

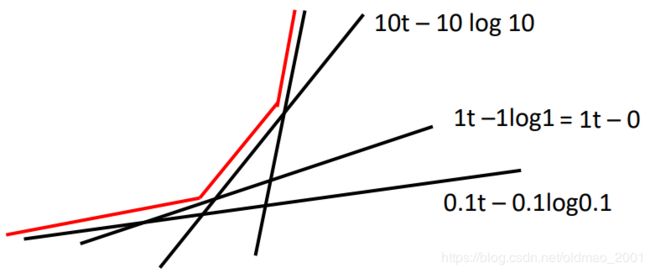
红线最后接近
$$f^{\ast }(t)=exp(t-1)$$
下面是数学证明，假设$f(x)=xlogx$
则：
$$f^{\ast }(t)=\underset{x\in dom(f)}{\max }\{xt-f(x)\}=\underset{x\in dom(f)}{\max }\{xt-xlogx\}\text{\hspace{1em}(1)}$$
令上式中$xt-xlogx=g(x)\text{, Given }t\text{, find }x\text{ maximizing }g(x)$
求极值，就是对$x$求导数等于0：
$$\begin{gathered} g^{\prime }(x)=t-logx-1=0 \\ x=exp(t-1) \end{gathered}$$
把上面内容代入公式（1）：
$$f^{\ast }(t)=xt-xlogx=exp(t-1)\times t-exp(t-1)\times (t-1)=exp(t-1)$$
一般化后：
$$(f^{\ast }{)}^{\ast }=f$$
讲这么多，下面看下上面两节内容和GAN的关系

Connection with GAN

通过上面的推导我们知道$f^{\ast }(t)$和$f(x)$互为Conjugate，写为：
$$f^{\ast }(t)=\underset{x\in dom(f)}{\max }\{xt-f(x)\}\leftarrow \to f(x)=\underset{t\in dom(f^{\ast })}{\max }\{xt-f^{\ast }(t)\}$$
这两个相互Conjugate的convex的函数有什么特别？我们继续看。
$$\begin{gathered} D_f(P||Q)={\int }_{x}q(x)f\left(\frac{p(x)}{q(x)}\right)dx \\ ={\int }_{x}q(x)\left(\underset{t\in dom(f^{\ast })}{\max }\left\{\frac{p(x)}{q(x)}t-f^{\ast }(t)\right\}\right)dx \end{gathered}$$
我们用函数$D(x)$代替$t$，使得输入x，输出为t，使得上面{}中的值最大，替换后，就找到了$D_f(P||Q)$的lower bound
$$\begin{gathered} D_f(P||Q)\ge {\int }_{x}q(x)\left(\frac{p(x)}{q(x)}D(x)-f^{\ast }(D(x))\right)dx \\ ={\int }_{x}p(x)D(x)dx-{\int }_{x}q(x)f^{\ast }(D(x))dx \end{gathered}$$
当我们找的函数$D(x)$是最好的，那么就可以逼近$D_f(P||Q)$
$$D_f(P||Q)\approx \underset{D}{\max }{\int }_{x}p(x)D(x)dx-{\int }_{x}q(x)f^{\ast }(D(x))dx$$
积分可以写成期望值：
$$=\underset{D}{\max }\{E_{x\sim P}[D(x)]-E_{x\sim Q}[f^{\ast }(D(x))]\}$$
接下来我们把$P=P_{data},Q=P_G$，则有：
$$D_f(P_{data}||P_G)=\underset{D}{\max }\{E_{x\sim P_{data}}[D(x)]-E_{x\sim P_G}[f^{\ast }(D(x))]\}$$
把上面的式子可以带回求Generator的公式：
$$\begin{array}{rl}{G}^{\ast }& =arg\underset{G}{\min }{D}_f(P_{data}||P_G)\\ & =arg\underset{G}{\min }\underset{D}{\max }\{E_{x\sim P_{data}}[D(x)]-E_{x\sim P_G}[f^{\ast }(D(x))]\}\\ & =arg\underset{G}{\min }\underset{D}{\max }V(G,D)\end{array}$$
也就是说我们可以优化不同的divergence（https://arxiv.org/pdf/1606.00709.pdf）


可以用来解决Mode Collapse

Mode Collapse

当我们的GAN模型Training with too many iterations……
有些人脸就会比较像，除了一些颜色不太一样

从数学上说就是我们的生成对象的分布越来越小了

Mode Dropping

就是真实数据有两簇或者多簇，但是生成数据只能生成其中一簇：

例如下面的人脸，一个循环只有白种人，一个循环只有黄种人，一个循环中只有黑人。

问题分析

传统的做法类似MLE实际上是最小化KL divergence，可以看到生成数据的分布是在真实数据中间，这也是为什么真实数据这么模糊

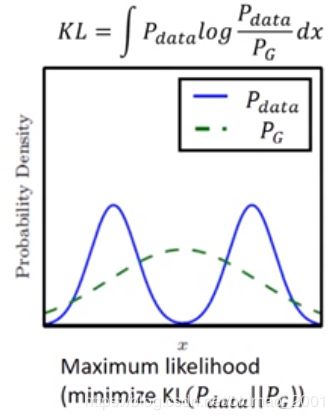
如果换成Reverse KL Divergence：

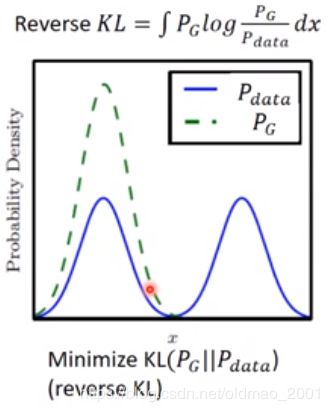
可以看到解决了模糊的问题，但是会出现Mode Dropping的问题。
因此选择不同的divergence对于GAN很重要。

解决Mode Collapse

Unsemble：训练多个generator，然后随机调一个generator来生成图片，这样结果就会比较diverse。
Train a set of generators: $\{G_1,G_2,\dots ,G_N\}$
To generate an image Random pick a generator $G_i$. Use $G_i$ generate the image.