引力搜索算法
最近在论文中看到有学者用改进的引力搜索算法解优化问题,有一个较好的效果,于是去了解了一下这个算法。
引力搜索算法(Gravitational Search Algorithm,GSA)是Esmat Rashedi等人在2009年提出的一种随机性启发式搜索算法,这种算法的灵感来自于牛顿的万有引力定律与运动定律:1.任意两个质点有通过连心线方向上的力相互吸引,该引力大小与它们质量的乘积成正比与它们距离的平方成反比。2.力使物体获得加速度。
在GSA中,质点被抽象成解空间的一个解,解之间存在一个相互吸引力,这个吸引力由解的质量与两个解之间的距离确定,质点的质量被抽象成解的评估函数值。在解空间中,每个解由其他解对其的吸引力获得加速度,质量更大(评估函数值更优)所提供的加速度更大,从而使解向更优解的方向移动。
看到这里,有些小伙伴会以为GSA是个与PSO差不多的算法,是的,GSA与PSO的外层框架是一致的,但是,它们最关键的粒子移动策略却是不同的:
1.在PSO中,粒子的移动只使用两个最佳位置pbest和gbest。但是在GSA中,智能体的方向是根据所有其他智能体或部分较优的智能体获得的总力来计算的。
2.PSO使用一种内存来更新速度(由于pbest和gbest)。然而,GSA是无内存的,只有智能体的当前位置在更新过程中起作用。
3.在PSO中,更新不考虑解之间的距离,而在GSA中,力与解之间的距离成反比。
4.PSO模拟了鸟类的社会行为,而GSA的灵感来自于物理现象。
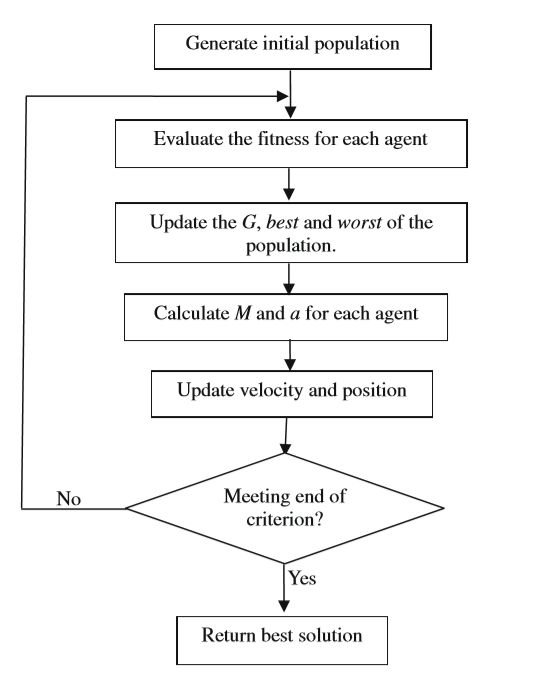
GSA的主要过程如下:
1. 确定搜索空间。
2. 随机初始化个体种群。
3. 对种群进行适应度评价。
4. 更新引力常量G,更新种群中最好的个体 best与最差的个体worst,更新个体的质量。
5. 计算每个个体在不同方向上的总引力。
6. 计算个体的加速度,基于此更新个体的速度。
7. 根据速度更新个体在解空间中的位置。
8. 重复步骤3-7直到达到停止标准。
具体的个体属性更新公式与引力计算公式建议参考 GSA: A Gravitational Search Algorithm这篇文章。
例: min z = x1 ** 2 + x2 ** 2
s.t. -10 <= x1 <= 10 , -10 <= x2 <= 10
# Gravitational Search Algorithm
import numpy as np
import random as rd
from math import exp, sqrt
'''min z = X1 ** 2 + X2 ** 2
s.t. -10 <= x1 <= 10
-10 <= X2 <= 10 '''
def init(n):
position, velocity = [], []
for i in range(n):
X1 = rd.uniform(-10, 10)
X2 = rd.uniform(-10, 10)
V1 = rd.uniform(-3, 3)
V2 = rd.uniform(-3, 3)
position.append([X1, X2])
velocity.append([V1, V2])
return position, velocity
def objFuntion(x1, x2):
return x1 ** 2 + x2 ** 2
def fitnessEva(position):
fitness = []
for i in range(len(position)):
fitness.append(objFuntion(position[i][0], position[i][1]))
return fitness
def findBestAndWorst(position):
return min(fitnessEva(position)), max(fitnessEva(position))
def calculateMass(fitness):
mass = []
Mass = []
for i in range(len(fitness)):
mass.append((fitness[i] - max(fitness)) / (min(fitness) - max(fitness)))
for i in range(len(mass)):
Mass.append(mass[i] / sum(mass))
return Mass
def calculateAcceleration(position, Mass, G, topK):
acceleration = []
Fi0, Fi1 = 0, 0
for i in range(len(position)):
for j in range(len(position)):
if i != j and j in topK:
Fi0 += rd.random() * G * ((Mass[i] * Mass[j]) / (calculateDistance(position[i], position[j]) + r)) * (
position[j][0] - position[i][0])
Fi1 += rd.random() * G * ((Mass[i] * Mass[j]) / (calculateDistance(position[i], position[j]) + r)) * (
position[j][1] - position[i][1])
if Mass[i] != 0:
acceleration.append([Fi0 / Mass[i] / 10, Fi1 / Mass[i] / 10]) #这里除10是为了避免粒子的加速度过大
else:
acceleration.append([10, 10])
Fi0 = 0
Fi1 = 0
return acceleration
def findTopK(fitness, K):
topK = []
dic = {}
for i in range(len(fitness)):
dic[i] = fitness[i]
fitness.sort()
for i in range(K):
topK.append(list(dic.keys())[list(dic.values()).index(fitness[i])])
return topK
def updateVelocityAndPosition(acceleration, position, velocity):
for i in range(len(velocity)):
velocity[i][0] = rd.random() * velocity[i][0] + acceleration[i][0]
velocity[i][1] = rd.random() * velocity[i][1] + acceleration[i][1]
position[i][0] = position[i][0] + velocity[i][0]
position[i][1] = position[i][1] + velocity[i][1]
def calculateDistance(p1,p2):
return sqrt((p1[0] - p2[0]) ** 2 + (p1[1] - p2[1]) ** 2)
def checkPosition(position):
for i in range(len(position)):
if position[i][0] < -10:
position[i][0] = -10
elif position[i][0] > 10:
position[i][0] = 10
if position[i][1] < -10:
position[i][1] = -10
elif position[i][1] > 10:
position[i][1] = 10
if __name__ == '__main__':
G = 100
r = 1
K = 50
iterx, maxIterx = 0, 50
position, velocity = init(50)
while iterx < maxIterx:
fitness = fitnessEva(position) #适应性评估
G = G * exp(-20 * iterx / maxIterx) #更新引力常量
Mass = calculateMass(fitness) #更新粒子质量
topK = findTopK(fitness, K) #找出适应度更优的前K个粒子
acceleration = calculateAcceleration(position, Mass, G, topK) #计算粒子加速度
updateVelocityAndPosition(acceleration, position, velocity) #根据加速度更新速度与位置
checkPosition(position) #检查粒子是否冲出了解空间
iterx += 1
K = K - iterx #更新K值
print(min(fitnessEva(position)))
print(position[fitnessEva(position).index(min(fitnessEva(position)))])
参考文献:
Rashedi E, Nezamabadi-pour H, Saryazdi S. GSA:a gravitational search algorithm[J].Information Science, 2009, 179 (13) :2232-2248.