LeetCode刷题第四周

这周不想多说话，有人，怕影响队友。

---

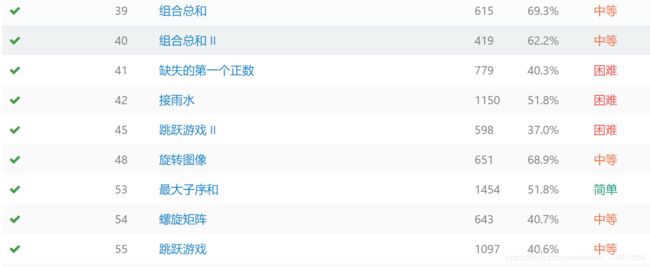
数组专题

简单

53. 最大子序和

题目链接： 点击跳转至本题

题目大意：
给定一个整数数组nums ，找到一个具有最大和的连续子数组(子数组最少包含一个元素)，要求返回其最大和。

解题思路：暴力查找 or 动态规划

方法1：暴力查找$O(n^2)$

// 方法1：双层for循环暴力查找
class Solution {
    public int maxSubArray(int[] nums) {
        //Integer.MIN_VALUE代表int类型能够表示的最小值
        int ans = Integer.MIN_VALUE;
        for(int i = 0;i < nums.length;i++){
            int sum = 0;
            for(int j = i;j < nums.length;j++){
                sum += nums[j];
                ans = Math.max(ans,sum);
            }
        }
        return ans;
    }
}

中等

39. 组合总和

题目链接：点击跳转至本题

题目大意：
给定一个无重复元素的candidates数组和一个目标值target，要求找出数组中所有可以使数字和为target的组合。
注意:

• candidates 中的数字可以无限制重复被选取。
• 所有数字(包括target)都是正整数。
• 解集不能包含重复的组合。

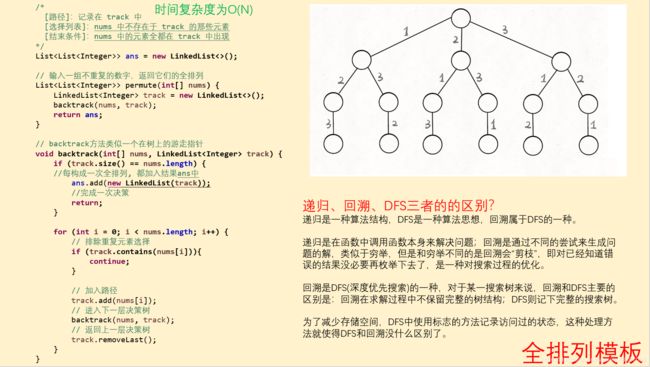
解题思路：递归算法+回溯思想

路　　径：track用来存储路径。
选择列表：target > candidates[i]。注意这里的target指的是本次循环内的target。
结束条件：target == 0。这里的target也是指本次循环内的target，因为target是在随着递归不断改变。

整体思路是对全排列模板的改动，其中backtrack的start参数是本层最开始元素的下标，因为数组中的数字可以无限制重复被选取(即可以取本身)，所以下一次的开始还是i。

class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        // ans用来存储结果
        List<List<Integer>> ans = new LinkedList<>();
        // 将路径记录在track中
        LinkedList<Integer> track = new LinkedList<>();
        backtrack(ans,track,candidates,target,0);
        return ans;
    }

    // backtrack方法类似一个树上的游走指针
    void backtrack(List<List<Integer>> ans,LinkedList<Integer> track,int[] candidates,int target,int start){
        // 每完成一次决策,都将结果加入ans,并退出本次backtrack
        if(target == 0){
            ans.add(new LinkedList(track));
            return;
        }
        for(int i = start;i < candidates.length;i++){
            if( target < candidates[i]){
                continue;
            }
            // 加入路径
            track.add(candidates[i]);
            // 进入下一层决策树
            backtrack(ans,track,candidates,target - candidates[i],i);
            // 返回上一层决策树
            track.removeLast();
        }
    }
}

40. 组合总和 II

题目链接： 点击跳转至本题

题目大意：
给定一个candidates数组和一给目标值target，要求找出数组中所有可以使数字和为 target的组合。
注意：

• 所有数字(包括目标数)都是正整数。
• 解集不能包含重复的组合。

解题思路：递归算法+回溯思想
路　　径：track用来存储路径。
选择列表：target > candidates[i] 。注意这里的target指的是本次循环内的target。
结束条件：target == 0。这里的target也是指本次循环内的target，因为target是在随着递归不断改变。

本题是39. 组合总和 的改版，不同点有两处：
①本题数组中每个数字在每个组合中只能使用一次， 因此backtrack方法的start参数的递归层(即下一次开始)是i+1。
②数组中的元素有重复， 因此先排序，再进行同层去重：if(i > start && candidates[i] == candidates[i - 1]) continue;

class Solution {
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        // ans用来存储结果
        List<List<Integer>> ans = new LinkedList<>();
        // 将路径记录在track中
        LinkedList<Integer> track = new LinkedList<>();
        Arrays.sort(candidates);
        backtrack(ans,track,candidates,target,0);
        return ans;

    }
    void backtrack(List<List<Integer>> ans,LinkedList<Integer> track,int[] candidates, int target, int start){
        // 每完成一次决策,都将结果加入ans,并退出本次backtrack
        if(target == 0){
            ans.add(new LinkedList(track));
            return ;
        }
        
        for(int i = start; i < candidates.length; i++){
            //同层去重：同一个位置的元素，与上一层相同，由于上一层已经考虑过，所以跳过
            if(i > start && candidates[i] == candidates[i - 1]){
                continue;
            } 
            // 因为是排过序的，当前元素大于目标值时，后面的元素肯定越来越大，直接返回，避免不必要的循环。
            if( target < candidates[i]){
                return;
            }
            // 加入路径
            track.add(candidates[i]);
            // 进入下一层决策树
            backtrack(ans,track,candidates,target - candidates[i],i+1);
            // 返回上一层决策树
            track.removeLast();
        }
    }
}

45. 跳跃游戏 II

题目链接： 点击跳转至本题

题目大意：
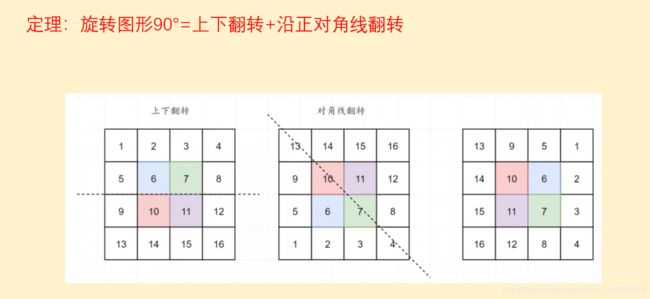
给定一个 n × n 的二维矩阵表示一个图像，要求将图像顺时针旋转 90 度。
注意：要求原地修改，即不能使用额外的矩阵来旋转图像。

解题思路：

class Solution {
    //正方形旋转90°，可通过上下翻转+正对角线翻转得到
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        //上下翻转
        for (int i = 0;i < n/2;i++) {
            int[] temp = matrix[i];
            matrix[i] = matrix[n - i - 1];
            matrix[n - i - 1] = temp;

        }

        //沿正对角线翻转
        for (int i = 0;i < n;i++) {
            for(int j = i + 1;j < n;j++){
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
    }
}

54. 螺旋矩阵

题目链接： 点击跳转至本题

题目大意：
给定一个包含 m x n 个元素的矩阵(m 行, n 列)，要求按照顺时针螺旋顺序，返回矩阵中的所有元素。

解题思路：图形系列-按层模拟
假设最外层矩阵是矩阵的第1层，从外部向内部逐层遍历打印矩阵，最外面一圈打印完，里面仍然是一个矩阵。需要注意的是当最内层矩阵仅是一行数，即i == (m-1-i)时的情况。这里i代表当前矩阵的上层行索引，(m-1-i)代表当前矩阵的下层行索引，一旦相等就代表最内侧只有一行数；同理，当最内层矩阵仅是一列数，即i == (n-1-i)时的情况。

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> list = new ArrayList<>();
        if(matrix == null || matrix.length == 0){
            return list;
        }
        //m行
        int m = matrix.length;
        //n列
        int n = matrix[0].length;
        //count层
        int count = (Math.min(m,n) + 1)/2;
        
        for(int i = 0;i < count ;i++){
            //从左上到右上
            for(int j = i;j < n - i;j++){
                list.add(matrix[i][j]);
            }
            //从右上到右下
            for(int j = i + 1;j < m - i ;j++){
                list.add(matrix[j][(n - 1) -i]);
            }

            //从右下到左下
            //(n - 1) - (i + 1)代表本层末行的倒数第二个数字
            //(n - 1) - i代表本层末行的最后一个数字
            for(int j = (n - 1) - (i + 1);j >= i && (i != (m - 1) - i);j--){
                list.add(matrix[(m - 1) - i][j]);
            }

            //从左下到左上
            for(int j = (m - 1) - (i + 1);j > i && (i != (n - 1) - i);j--){
                list.add(matrix[j][i]);
            }
        }
        return list;
    }
}

55. 跳跃游戏

题目链接： 点击跳转至本题

题目大意：
给定一个非负整数数组，最初位于数组的第一个位置。数组中的每个元素代表在该位置可以跳跃的最大长度。要求判断是否能够到达最后一个位置，结果返回true或false

解题思路：贪心算法
从左到右遍历数组，针对每个位置i，判断其是否可以到达最后。在遍历过程中，如果最远可以到达的位置>数组的最后一个位置就返回true；否则，i值后移并且更新当前最远可以到达的位置，继续遍历。

class Solution {
    public boolean canJump(int[] nums) {
        //当前最大能跳跃的长度
        int maxJump = 0;
        for (int i = 0; i < nums.length; i++) {
            if (i <= maxJump) {
                maxJump = Math.max(maxJump, i + nums[i]);
                if (maxJump >= nums.length - 1) {
                    //如果跳到最后或跳出数组
                    return true;
                }
            }
        }
        return false;
    }
}

困难

如果数组中的数 <= 0，或 >=n+1，则1~n(n指数组的长度)中必定会有数字缺失。

41. 缺失的第一个正数

题目链接： 点击跳转至本题

题目大意：
给定一个未排序的整数数组，要求找出其中没有出现的最小的正整数。
要求的算法时间复杂度应为O(n)。

解题思路：

方法1：双层for循环
外层循环1-n，内层循环遍历数组，也就是拿数字1-n依次在数组中匹配，每匹配到一个就将数字对应的标志变量flag置为true，紧接着开始判断此flag的值，若为false则代表没有匹配到，直接返回。额外的，如果全部值都匹配到了，则代表数组中的数正好就是1-n，此时返回nums.length+1。此种方法较为简单，但时间复杂度为O(n^2)。

//方法1：双层for循环
class Solution {
    public int firstMissingPositive(int[] nums) {
        //外层循环1-n
        for(int i = 1;i <= nums.length;i++){
            boolean flag = false;
            //内层循环遍历数组
            for(int j = 0;j < nums.length;j++){
                if(i == nums[j]){
                    flag = true;
                    break;
                }
            }
            if(flag == false){
                return i;
            }
        }     
        return nums.length + 1;
    }
}

42. 接雨水

题目链接： 点击跳转至本题

题目大意：
给定一个非负整数的数组，每个数代表宽度为1的柱子的高度，求此数组对应的柱子，在下雨后能接多少雨水。

解题思路：双指针
首先需要明白下面几个点：
left：从左往右处理的当前下标
right：从右往左处理的当前下标
left_max：left指针左边的最大值
right_max：right指针右边的最大值

• 在某个位置index处，它能存的水，取决于它左右两边的最大值中较小的一个，即为max-height[index]。
• 对于指针left而言，它左边最大值一定是left_max，右边最大值却是大于等于right_max的。此时，如果left_max
• 同理，对于指针right而言，它右边最大值一定是right_max，左边最大值却是大于等于left_max的。此时，如果left_max>right_max成立，那么它就知道自己能存多少水了。无论左边将来会不会出现更大的left_max，都不影响这个结果。

class Solution {
    public int trap(int[] height) {
        // 指针l和r分别位于数组的两端
        int l = 0,r = height.length - 1;
        //max_l代表l指针左边的最大值，max_r代表r右边的最大值
        int max_l = 0,max_r = 0;
        int ans = 0;
        while(l <= r){
            if(max_l < max_r){
                if(height[l] < max_l){
                    ans += max_l-height[l];
                } else if(height[l] >= max_l) {
                    //更新max_l
                    max_l = height[l];
                }
                l++;
            }else if(max_l >= max_r) {
                if(height[r] < max_r){
                    //
                    ans += max_r-height[r];
                }else if(height[r] >= max_r){
                    //更新max_r
                    max_r=height[r];
                }
                r--;
            }
        }
        return ans;
    }
}

45. 跳跃游戏 II

题目链接： 点击跳转至本题

题目大意：
给定一个非负整数数组，数组中的每个元素代表你在该位置可以跳跃的最大长度，你最初位于数组的第一个位置。要求使用最少的跳跃次数到达数组的最后一个位置。这个最少的次数是多少？

解题思路：贪心算法
在遍历过程中，维护当前能够到达的最大下标maxPosition，将其记为下一次的起跳点nextjump，每到达下一次起跳点时，更新下一次起跳点并将跳跃次数+1。

class Solution {
    public int jump(int[] nums) {
        //记录当前能到达的最大下标
        int maxPosition = 0;
        //记录下次起跳位置
        int nextjump = 0;
        //记录结果
        int ans = 0;

        for(int i = 0;i < nums.length - 1;i++){
            //更新下一步能到达的最远下标
            maxPosition = Math.max(maxPosition,i + nums[i]);
            //到达下一次起跳位置时
            if(i == nextjump){
                //更新下一次起跳位置
                nextjump = maxPosition;
                //计数器+1
                ans++;
            }
        }
        return ans;
    }
}

题目链接： 点击跳转至本题

题目大意：

解题思路：

题目链接： 点击跳转至本题

题目大意：

解题思路：