解码斯坦福开源狗DogGo--附硬件清单、源码、图纸、论文

转载注明出处

一.DogGo介绍

 

DogGo是由斯坦福学生机器人俱乐部（Stanford Student Robotics club）Extreme Mobility 团队设计并打造，全名为 Stanford Doggo 的四足机器人。这个机器人能跳 1 米多高，还能表演后空翻。与其他四足机器人动辄上万美元的成本不同，这个机器人的成本降到了 3000 美元以下。设计团队在2019年初陆续开源了该机器人的设计图、代码以及材料清单。

Stanford Doggo采用并行腿控制，每一条腿为2个自由度，一共为8个自由度。目前在所有机器人中保持着最高弹跳记录。成本低、结构简单，几乎所有的组件都能在线上获取。当然，相比于波士顿动力、Laikago、浙大的绝影、MIT的小狗而言，它没有强大的硬件支持和更复杂的控制系统，但是单从研发时间、研发成本、以及最终效果来说，斯坦福的DogGo绝对是性价比最高的四足机器人。

Stanford Doggo

二.相关链接

1. Stanford Doggo github 总地址
2. Stanford Doggo 源码 github地址
3. Stanford Doggo CAD图纸 github地址
4. ODrive驱动器 github地址
5. ODrive 驱动器官网
6. Stanford Doggo 论文原址

如果嫌上面网站麻烦，也可以直接在CSDN上下载：

7. Stanford DogGo源码、图纸CSDN下载链接
8. Stanford DogGo论文
9. Stanford DogGo 硬件清单
    

三.硬件解析

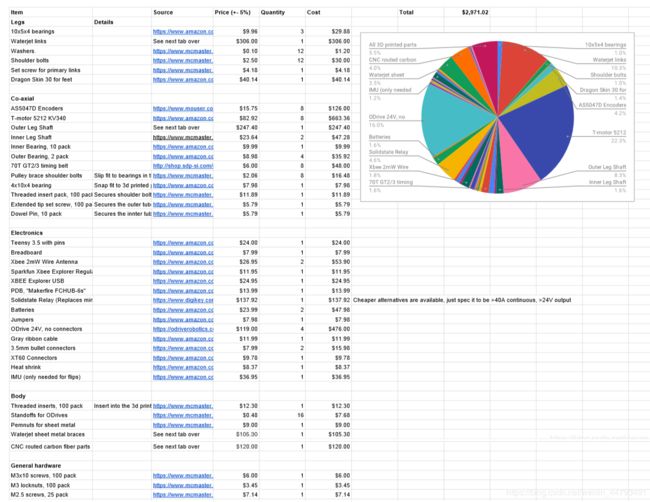
以上是官方给的所有硬件的清单，想要PDF文档的话可以在这下载（硬件清单）看上去很多，但其实最最核心的硬件不过就下面列出的：

材料	数量
Teensy 3.5（单片机）	1
ODrives（驱动器）	4
TMotor MN5212（电机）	8
Sparkfun BNO080 IMU （陀螺仪）	1
Xbee（遥控器）	1
Gigavac P105 Mini-Tactor（继电器）	1
其他（碳纤维板、齿带、连杆、轴承等等）	······

 

 
 
各硬件连接如下：

注：Battery为电池    Relay为继电器     PDB为分电板    microcontroller为Teensy 3.5    M为电机      XBee为遥控器
 

1. Doggo有四个v3.5、48V ODrives，每条腿两个，安装在碳纤维侧板上。中间的2mm碳纤维板上，有一个Teensy 3.5，一个Sparkfun BNO080 IMU和一个5mW的Xbee。

2. Teensy通过四条独立的UART线与ODrives对话，每条线路的工作频率为500000波特。在这个板块下面，有配电板和一个Gigavac P105 Mini-Tactor继电器，所以可以使用一个外接的ESTOP开关来关闭机器人电源。Doggo还有两个1000mah 6s Tattu锂电池。

3. 它的工作方式是在碳纤维侧板上安装了两个TMotor MN5212电机。这些电机每秒重复计算8000次，通过感应机器人外力的电机帮助确定每条腿应该施加多大的力和扭矩。

4. 团队还加了一个3D打印轴承座，有两个轴承来固定外同轴管。如下图所示：

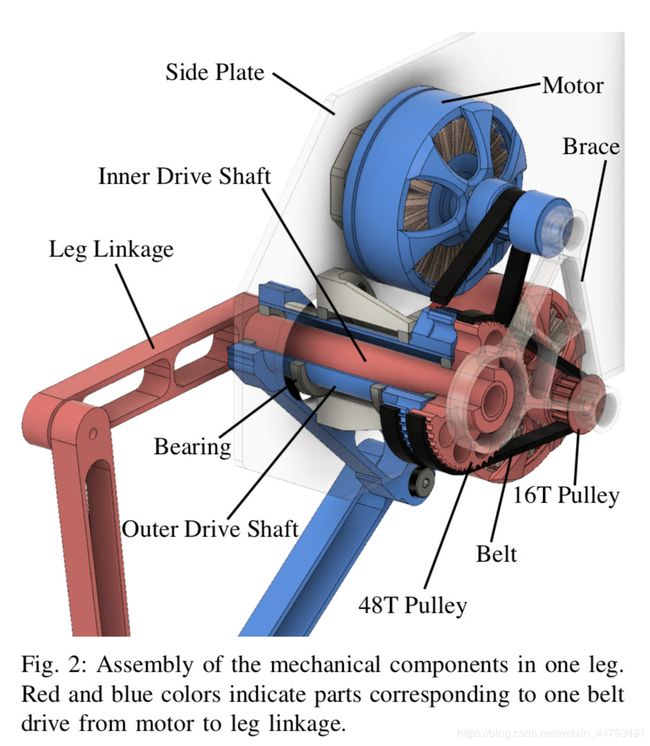
两个电机通过16T皮带轮和48T皮带轮之间的GT2皮带将动力传递给同轴皮带，每根皮带6mm宽，间距3mm间距。

5. 由于预算有限，团队并没有使用现成滑轮，而是使用Xometry SLS服务（在线3D打印服务）自己打印出轴承座。不过一定要准确地调整Xometry SLS服务，如果部件以一定角度打印，则由于偏角层，滑轮齿的几何形状会变形。

四.软件解析

运动控制系统是是整个电子狗最最核心的部分，四足的运动控制系统门槛一般很高。不过在这方面，Stanford Doggo 还是很友好的。相比于其他四足，DogGo的运动控制系统比较简单。如果日后想要研究更复杂的四足控制系统，那么拿它入门还是非常有意义的。
 

先来看看Stanford Doggo的代码结构：

主要还是讲我对DogGo步态控制的理解，即是上图中“position_control”的文件.“position_control”是整份源码的核心，其他文件要不就是为他服务（像globals、uart）,要不就是它的拓展（像backflip、jump）。

 
1. DogGo的步态参数分为stance_height、down_amp、up_amp、flight_percent、step_length、freq、step_diff，通过步态参数的不同就能实现Tror 、Bound、 Walk、Pronk、Dance、Hop、 Flip、Turn_Tror 等各种步态。

/*步态参数*/
struct GaitParams {
    float stance_height = 0.18; //步行时身体与地面的期望高度(m)    *Desired height of body from ground during walking (m)
    float down_amp = 0.00; //正弦轨迹低于stanceHeight的峰值振幅(m) *Peak amplitude below stanceHeight in sinusoidal trajectory (m)
    float up_amp = 0.06; //在正弦轨迹中，足部峰值在支架高度以上(m) *Height the foot peaks at above the stanceHeight in sinusoidal trajectory (m)
    float flight_percent = 0.6;//飞行相时间占比     *Portion of the gait time should be doing the down portion of trajectory
    float step_length = 0.0; //全步长(m)      *Length of entire step (m)
    float freq = 1.0; //一个步态周期的频率(Hz)   *Frequency of one gait cycle (Hz)
    float step_diff = 0.0; //左腿步长与右腿步长之差    *difference between left and right leg step length
};

/*各种步态的参数*/
struct GaitParams state_gait_params[] = {
    //{s.h, d.a., u.a., f.p., s.l., fr., s.d.}
    {NAN, NAN, NAN, NAN, NAN, NAN, NAN}, // STOP       
    {0.17, 0.04, 0.06, 0.35, 0.15, 2.0, 0.0}, // TROT  
    {0.17, 0.04, 0.06, 0.35, 0.0, 2.0, 0.0}, // BOUND  
    {0.15, 0.00, 0.06, 0.25, 0.0, 1.5, 0.0}, // WALK   
    {0.12, 0.05, 0.0, 0.75, 0.0, 1.0, 0.0}, // PRONK   
    {NAN, NAN, NAN, NAN, NAN, NAN, NAN}, // JUMP       
    {0.15, 0.05, 0.05, 0.35, 0.0, 1.5, 0.0}, // DANCE  
    {0.15, 0.05, 0.05, 0.2, 0.0, 1.0, 0.0}, // HOP    
    {NAN, NAN, NAN, NAN, NAN, 1.0, NAN}, // TEST      
    {NAN, NAN, NAN, NAN, NAN, NAN, NAN}, // ROTATE    
    {0.15, 0.07, 0.06, 0.2, 0.0, 1.0, 0.0}, // FLIP   
    {0.17, 0.04, 0.06, 0.35, 0.1, 2.0, 0.06}, // TURN_TROT 
    {NAN, NAN, NAN, NAN, NAN, NAN, NAN} // RESET  
};

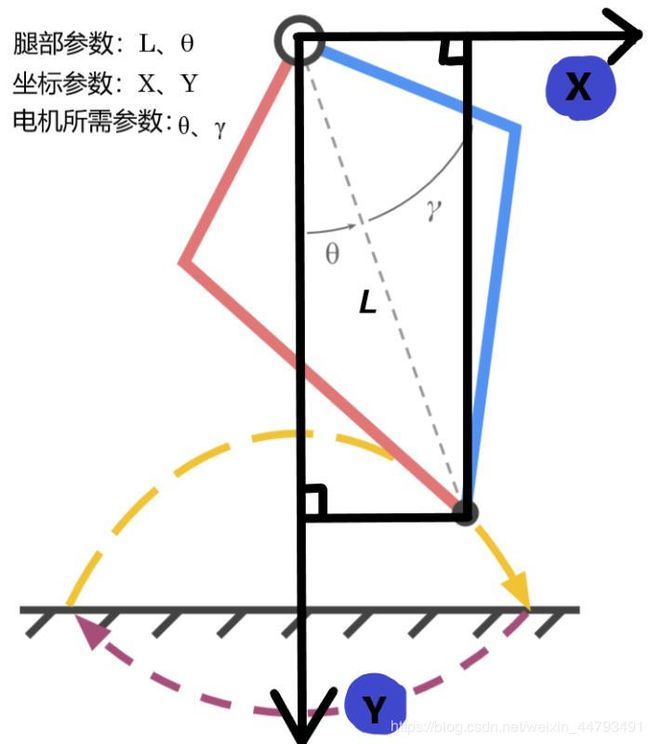
2. 步态参数采用的是笛卡尔坐标系（直角坐标系），但是在研究腿部轨迹的时候需要将直角坐标系转化为极坐标系，即将X、Y转化为L、θ。电机需要的是转角，所以还需要将L、θ转化为θ和γ，发送给ODrive最终就能实现足端到预期位置。（腿部连杆长度已知，所以只需要用余弦定理就能在三种参数间相互转化）

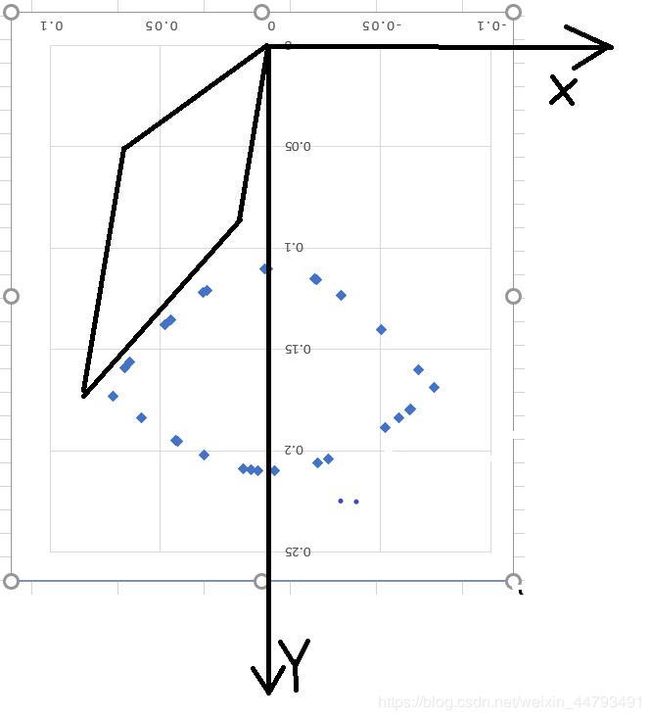
3. 运动轨迹用的是正弦函数，通过所给的步态参数可以求出预期的正弦轨迹的函数，分为上下两段（如上图黄色和紫色的两条轨迹），然后在对应时间内输出对应坐标就能实现腿部运动。

图一是我将源码移植到stm32进行仿真，记录输出的X、Y，打印在表格上。上下两段正弦轨迹可以通过修改步态参数进行调整。

图二是在仿真时输出各腿的θ、γ参数（放大了100倍）。（注：X、Y为正弦函数，但是θ、γ并非正弦分布）

/*DogGo的正弦轨迹发生器，即将步态参数转化为正弦轨迹的具体步骤*/

void SinTrajectory (float t, struct GaitParams params, float gaitOffset, float& x, float& y) {
    static float p = 0;
    static float prev_t = 0;

    float stanceHeight = params.stance_height;//直立高度
    float downAMP = params.down_amp;//下幅值
    float upAMP = params.up_amp;//上幅值
    float flightPercent = params.flight_percent;//飞行相占比
    float stepLength = params.step_length;//步长
    float FREQ = params.freq;//频率

    p += FREQ * (t - prev_t < 0.5 ? t - prev_t : 0); // should reduce the lurching when starting a new gait
    prev_t = t;

    float gp = fmod((p+gaitOffset),1.0); //mod(a,m)返回a除以m的余数  mod(a,m) returns remainder division of a by m
    if (gp <= flightPercent) {
        x = (gp/flightPercent)*stepLength - stepLength/2.0;
        y = -upAMP*sin(PI*gp/flightPercent) + stanceHeight;
    }
    else {
        float percentBack = (gp-flightPercent)/(1.0-flightPercent);
        x = -percentBack*stepLength + stepLength/2.0;
        y = downAMP*sin(PI*percentBack) + stanceHeight;
    }
}

---

如果对我讲的似懂非懂，建议还是去github去看看它的源码吧，毕竟我介绍的只是DogGo其中的一部分,还有很多东西需要自己去琢磨。