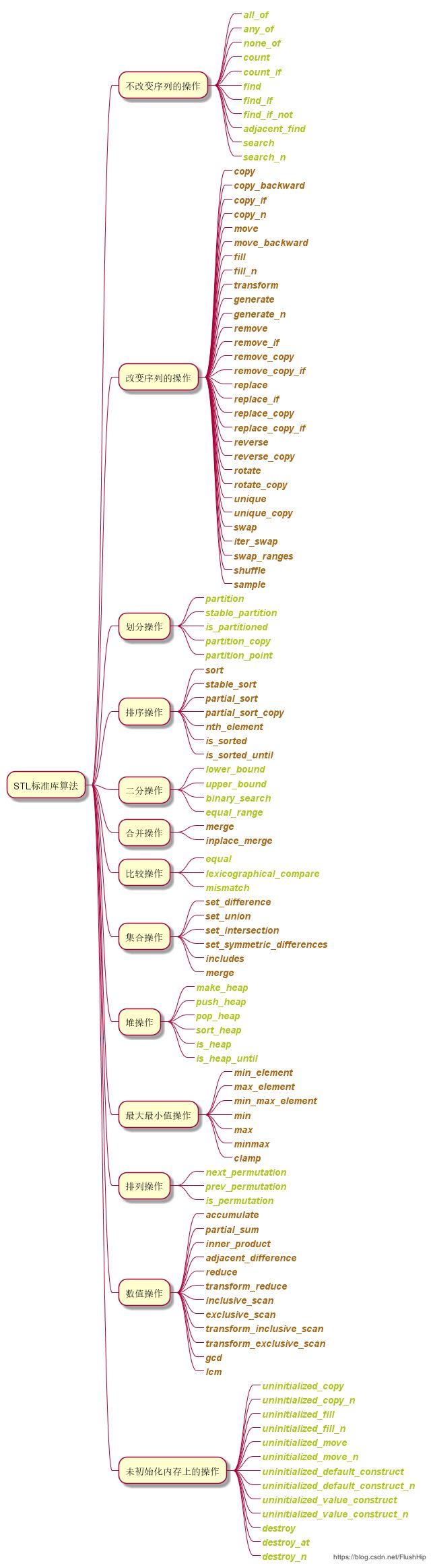
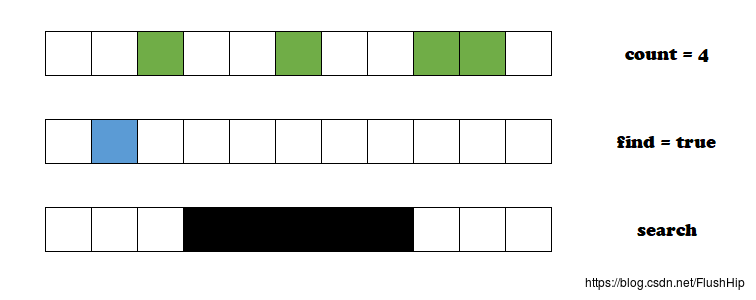图解STL中算法的分类、简介及其Demo

STL中包含算法头文件就可以使用其中的算法了，使用这些通用的算法可以使得代码更加简单、易读、通用。但是这些算法有哪些呢？以及这些算法的职能又是什么？其实这些东西，候捷大师在他的《STL源码剖析》中都有列举，且FluentCPP有一篇文章105 STL Algorithms in Less Than an Hour，他也给STL的105个算法分了七个大类。我这里总结了下他们的分类，自己按STL算法所设计的方面进行了一个大致分类，其中很多算法都同时在几个类中。

• 不改变序列的操作
• 改变序列的操作
• 划分操作
• 排序操作
• 二分操作
• 合并操作
• 比较操作
• 集合操作
• 堆操作
• 最大最小值操作
• 排列操作
• 数值操作
• 未初始化内存上的操作

这里不说具体怎么使用每个算法，但是使用的Demo会给出来，使用方法都可以在https://en.cppreference.com查到；这里也不说每个算法的实现原理，实现原理后面还会写博客说的。

来张总结图吧，可以对函数有个大体的印象。

先说明下，算法中带_if后缀的表示可自定义条件，带_copy后缀的表示把结果放入新的序列中，带_n后缀的表示操作相同元素n次。

*_copy :

*_if：

*_n：

这些都是标准库的带后缀的例子，在下面的博文中，不会对这些内容再过多赘述。

不改变序列的操作

• all_of
• any_of
• none_of
• count
• count_if
• find
• find_if
• find_if_not
• adjacent_find
• search
• search_n

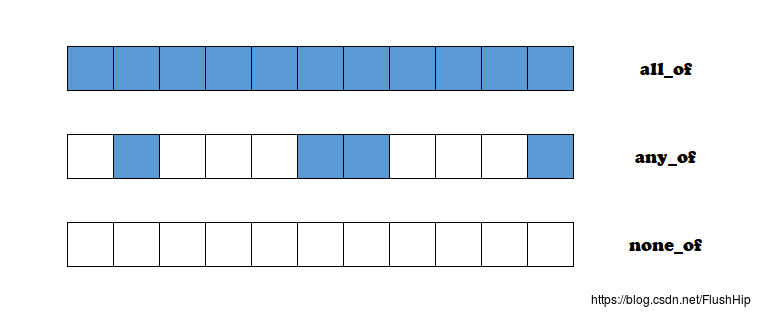
(all / any / none)_of

这是C++11新增的三个算法，分别表示序列上所有的元素全部都是……，存在一个是……，没有一个是……。

find / count / search

count对序列中指定元素进行计数，加了_if的版本可以自定义计数条件；

find在序列中顺序查找一个元素，同理，加了_if的版本可以自定义查找条件，_if_not(C++11)是_if的方面，把查找条件取反；

search在序列中查找一段连续子序列，加了_n表示在序列中查找一段连续相同的子序列。

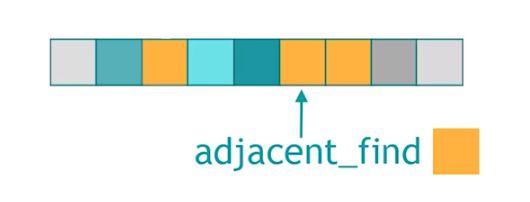
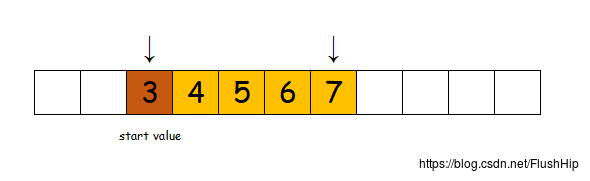
adjacent_find

在序列中找到第一个挨在一起的两个一样值的指定元素，看图就明白了。

Demo

void NonModifySequenceDemo()
{
    std::vector result {2, 0, 4, 8, 6};

    std::cout << "{2, 0, 4, 8, 6} all_of even " << std::boolalpha <<
            std::all_of(std::begin(result), std::end(result), [] (const int & ele)
    {
        return ele % 2 == 0;
    }) << std::endl;

    for_each(std::begin(result), std::end(result), [] (int & ele)
    {
        --ele;
    });

    std::cout << "{1, -1, 3, 7, 5} any_of even " << std::boolalpha <<
            std::any_of(std::begin(result), std::end(result), [] (const int & ele)
    {
        return ele % 2 == 0;
    }) << std::endl;

    std::cout << "{1, -1, 3, 7, 5} none_of even " << std::boolalpha <<
            std::none_of(std::begin(result), std::end(result), [] (const int & ele)
    {
        return ele % 2 == 0;
    }) << std::endl;

    std::cout << "{1, -1, 3, 7, 5} has " <<
            std::count(std::begin(result), std::end(result), 1) << " numbers of 1" << std::endl;

    std::cout << "{1, -1, 3, 7, 5} has " <<
            std::count_if(std::begin(result), std::end(result), [] (const int & ele)
    {
        return ele % 2;
    }) << " numbers of odd" << std::endl;

    std::cout << "{1, -1, 3, 7, 5} the first equal 3 at " <<
            std::find(std::begin(result), std::end(result), 3) - std::begin(result) <<
            " index" << std::endl;

    std::cout << "{1, -1, 3, 7, 5} the first greater 6 at " <<
            std::find_if(std::begin(result), std::end(result), [] (const int & ele)
    {
        return ele > 6;
    }) - std::begin(result) << " index" << std::endl;

    std::cout << "{1, -1, 3, 7, 5} the first not greater 0 at " <<
            std::find_if_not(std::begin(result), std::end(result), [] (const int & ele)
    {
        return ele > 0;
    }) - std::begin(result) << " index" << std::endl;

    result[3] = 3;
    std::cout << "{1, -1, 3, 3, 5} adjacent equal value is " <<
            *std::adjacent_find(std::begin(result), std::end(result)) <<
            std::endl;

    result.clear();
    result = {4, 3, 6, 6, 6, 6, 9, 1, 2, 4, 10};
    std::vector tag {1, 2, 4};

    std::cout << "{4, 3, 6, 6, 6, 6, 9, 1, 2, 4, 10} include {1, 2, 4} at " <<
            std::search(std::begin(result), std::end(result),
                        std::begin(tag), std::end(tag)) - std::begin(result) <<
            " index" << std::endl;

    std::cout << "{4, 3, 6, 6, 6, 6, 9, 1, 2, 4, 10} include 4 numbers of six at " <<
            std::search_n(std::begin(result), std::end(result),
                        4, 6) - std::begin(result) <<
            " index" << std::endl;
}

改变序列的操作

• copy / copy_backward
• copy_if / copy_n(C++11)
• move / move_backward(C++11)
• fill / fill_n
• transform
• generate / generate_n
• remove / remove_if / remove_copy / remove_copy_if
• replace / replace_if / replace_copy / replace_copy_if
• reverse / reverse_copy
• rotate / rotate_copy
• unique / unique_copy
• swap / iter_swap / swap_ranges
• shuffle(C++11)
• sample(C++17)

改变序列的算法最多了，相应地，这些操作都提供了几个待后缀的函数。

先来讲几个常见的同时也是用得比较多的。

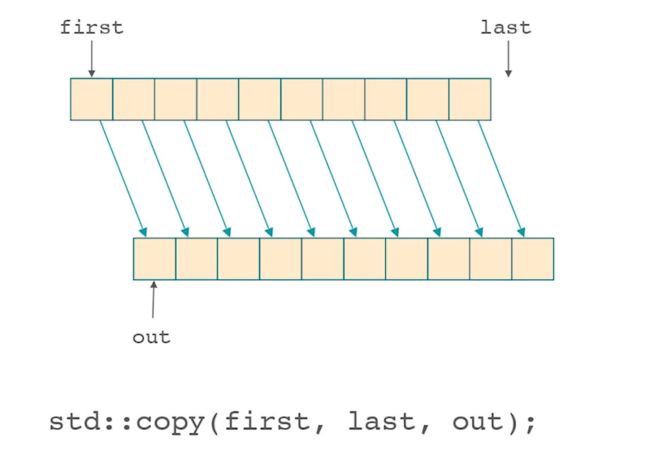
copy

复制。

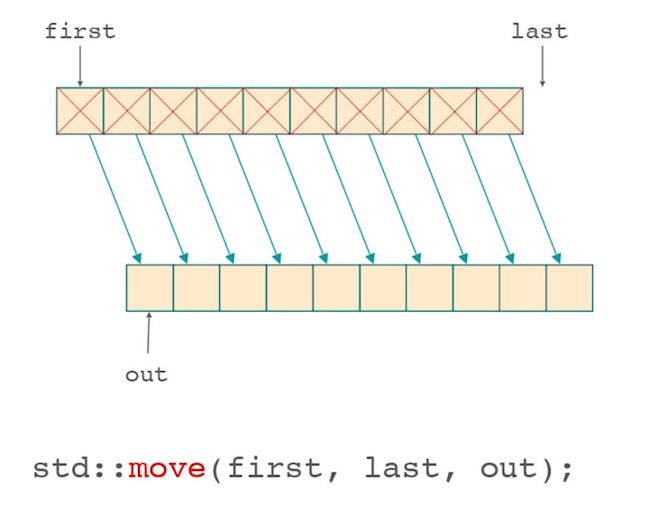
move

这个move并不是取得一个值的右值引用，而是取得整个序列的右值引用。

下面是我自己做的图：

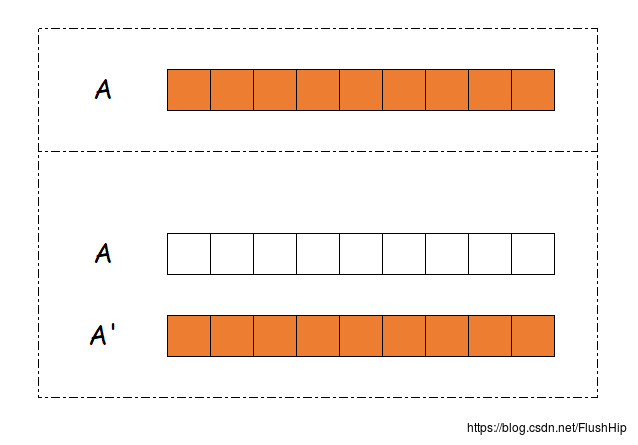
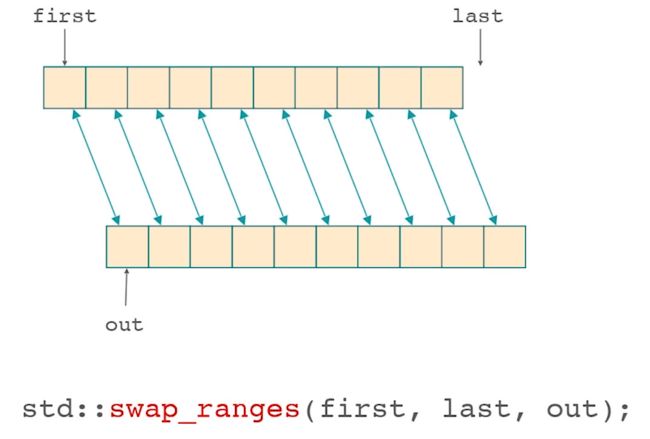
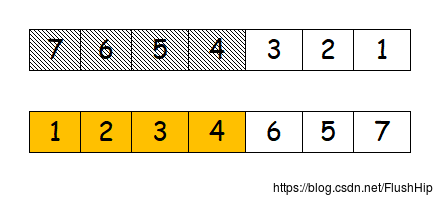
swap_ranges

交换两个序列的内容。

类似的还有swap，这个用得最多；iter_swap可以交换指针或者迭代器指向内存的内容。

fill

类似memset。

generate

这个和fill挺像，只不过generate使用一个函数往序列中填充元素，也就是说你可以定制这个序列。

iota

iota的功能是在一段区间上填上递增的数字。

下面是我绘制的图：

remove

你以为remove的作用类似下图吗？删掉指定的元素。

不，它只是把要删除的元素移动到了序列尾。

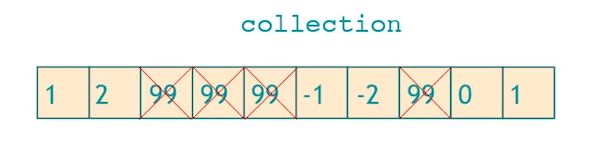
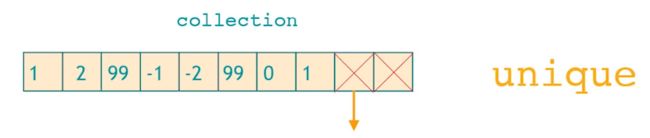
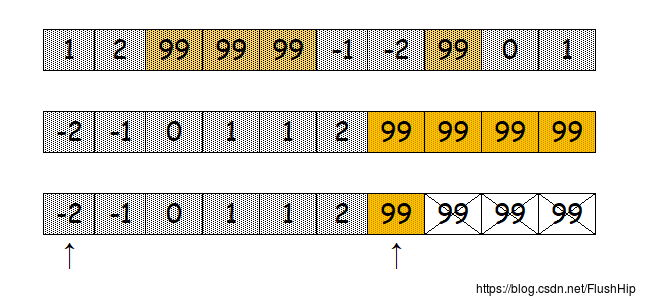
unique

删除序列中连续重复的内容，和remove类似，只是把冗余的元素移动过了序列尾。

注意，上图中并没有删除最后一个99，如果想要删除序列中重复的内容，需要先对序列调用std::sort使冗余的元素聚集在一起。

transform

对序列中的每个元素都执行函数f，可以对序列本身没有影响，也可以改变序列本身。看看transform的声明就知道了。

template< class InputIt, class OutputIt, class UnaryOperation >
OutputIt transform( InputIt first1, InputIt last1, OutputIt d_first,
                    UnaryOperation unary_op );

for_each

和transform有点像，它也是对序列执行函数f。只不过for_each在本序列上进行操作，它没有transform的灵活性，因此对序列产生副作用的机率很大。也看看这个算法的声明：

template< class InputIt, class UnaryFunction >
UnaryFunction for_each( InputIt first, InputIt last, UnaryFunction f );

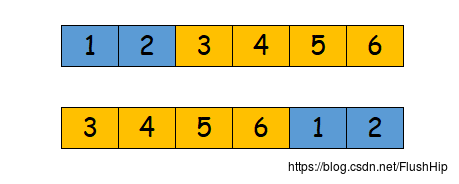
rotate

在序列中交换其中的两部分的顺序。

reverse

反转序列。

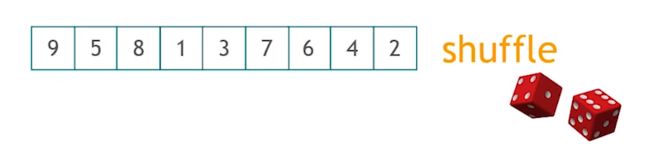
shuffle

正如下图所示，有一个骰子，对一个序列调用shuffle会随机打乱这个序列元素之间的顺序。

sample

这是C++17的内容，作用是从序列中随机挑选n个元素出来组成新的序列，每个元素只会被选择一次，如果n大于序列的长度，那么整个序列都会被选出来。

Demo

void ModifySequenceDemo()
{
    static const int LEN = 10;

    std::vector res(5), aux(LEN);
    std::iota(res.begin(), res.end(), 1);
    std::copy(res.begin(), res.end(), aux.begin());

    std::cout << "copy {1, 2, 3, 4, 5} to aux(10) : {";
    for (auto it = aux.begin(); it != aux.end(); std::cout << *it <<
            std::array{", ", "}\n"}[it + 1 == aux.end()], ++it) {}

    aux.clear(), aux.resize(LEN, 0);

    std::copy_backward(res.begin(), res.end(), aux.end());

    std::cout << "copy_backward {1, 2, 3, 4, 5} to aux(10) : {";
    for (auto it = aux.begin(); it != aux.end(); std::cout << *it <<
            std::array{", ", "}\n"}[it + 1 == aux.end()], ++it) {}

    aux.clear(), aux.resize(LEN, 0);

    std::copy_if(res.begin(), res.end(), aux.begin(), [] (const int & ele)
    {
        return ele % 2;
    });

    std::cout << "copy_if {1, 2, 3, 4, 5} to aux(10) : {";
    for (auto it = aux.begin(); it != aux.end(); std::cout << *it <<
            std::array{", ", "}\n"}[it + 1 == aux.end()], ++it) {}

    aux.clear(), aux.resize(LEN, 0);

    std::copy_n(res.begin(), 3, aux.end());

    std::cout << "copy_n(3) {1, 2, 3, 4, 5} to aux(10) : {";
    for (auto it = aux.begin(); it != aux.end(); std::cout << *it <<
            std::array{", ", "}\n"}[it + 1 == aux.end()], ++it) {}

    std::fill_n(res.begin(), 3, 3);

    std::cout << "fill_n(3) {1, 2, 3, 4, 5} : {";
    for (auto it = res.begin(); it != res.end(); std::cout << *it <<
            std::array{", ", "}\n"}[it + 1 == res.end()], ++it) {}

    res.clear(), res.resize(LEN >> 1, 0);

    std::fill(res.begin(), res.end(), 0);

    std::cout << "fill {} by 0 : {";
    for (auto it = res.begin(); it != res.end(); std::cout << *it <<
            std::array{", ", "}\n"}[it + 1 == res.end()], ++it) {}

    // res.clear(), res.resize(LEN >> 1, 0);

    std::transform(res.begin(), res.end(), res.begin(), [] (const int & ele)
    {
        return ele + 1;
    });

    std::cout << "transform {0, 0, 0, 0, 0} to {1, 1, 1, 1, 1} : {";
    for (auto it = res.begin(); it != res.end(); std::cout << *it <<
            std::array{", ", "}\n"}[it + 1 == res.end()], ++it) {}

    res.clear(), res.resize(LEN >> 1, 0);

    std::generate(res.begin(), res.end(), [] ()
    {
        static int cnt = 1;
        return cnt++;
    });

    std::cout << "generate {} : {";
    for (auto it = res.begin(); it != res.end(); std::cout << *it <<
            std::array{", ", "}\n"}[it + 1 == res.end()], ++it) {}

    res.clear(), res.resize(LEN >> 1, 0);

    std::generate_n(res.begin(), LEN >> 1, [] ()
    {
        return std::rand() & 0x7fffffff;
    });

    std::cout << "generate_n {} random : {";
    for (auto it = res.begin(); it != res.end(); std::cout << *it <<
            std::array{", ", "}\n"}[it + 1 == res.end()], ++it) {}

    res.clear(), res.resize(LEN >> 1, 0);

    res = {5, 5, 5, 4, 5};

    res.erase(std::remove(res.begin(), res.end(), 5), res.end());

    std::cout << "remove 5 from {5, 5, 5, 4, 5} : {";
    for (auto it = res.begin(); it != res.end(); std::cout << *it <<
            std::array{", ", "}\n"}[it + 1 == res.end()], ++it) {}

    res = {5, 1, 5, 4, 5};

    std::replace(res.begin(), res.end(), 5, 6);

    std::cout << "repalce 5 with 6 from {5, 1, 5, 4, 5} : {";
    for (auto it = res.begin(); it != res.end(); std::cout << *it <<
            std::array{", ", "}\n"}[it + 1 == res.end()], ++it) {}

    res = {1, 2, 3, 4, 5};

    std::reverse(res.begin(), res.end());

    std::cout << "reverse {1, 2, 3, 4, 5} : {";
    for (auto it = res.begin(); it != res.end(); std::cout << *it <<
            std::array{", ", "}\n"}[it + 1 == res.end()], ++it) {}

    res = {1, 2, 3, 4, 5};

    std::rotate(res.begin(), res.begin() + 2, res.end());

    std::cout << "rotate {1, 2, 3, 4, 5} that {1, 2}, {3, 4, 5} : {";
    for (auto it = res.begin(); it != res.end(); std::cout << *it <<
            std::array{", ", "}\n"}[it + 1 == res.end()], ++it) {}

    res = {5, 5, 5, 4, 5};

    res.erase(std::unique(res.begin(), res.end()), res.end());

    std::cout << "unique from {5, 5, 5, 4, 5} : {";
    for (auto it = res.begin(); it != res.end(); std::cout << *it <<
            std::array{", ", "}\n"}[it + 1 == res.end()], ++it) {}

    res = {1, 2, 3, 4, 5};

    std::shuffle(res.begin(), res.end(), std::mt19937{std::random_device{}()});

    std::cout << "shuffle {1, 2, 3, 4, 5} : {";
    for (auto it = res.begin(); it != res.end(); std::cout << *it <<
            std::array{", ", "}\n"}[it + 1 == res.end()], ++it) {}

#if __cplusplus >= 201702L
    res = {1, 2, 3, 4, 5};
    aux.clear();

    std::sample(res.begin(), res.end(),
                std::back_inserter(aux),
                3,
                std::mt19937{std::random_device{}()});

    std::cout << "sample {5, 1, 5, 4, 5} 3 elements: {";
    for (auto it = aux.begin(); it != aux.end(); std::cout << *it <<
            std::array{", ", "}\n"}[it + 1 == res.end()], ++it) {}
#endif // __cplusplus
}

划分操作

• partition
• stable_partition
• is_partitioned(从此向下都是C++11的新增算法)
• partition_copy
• partition_point

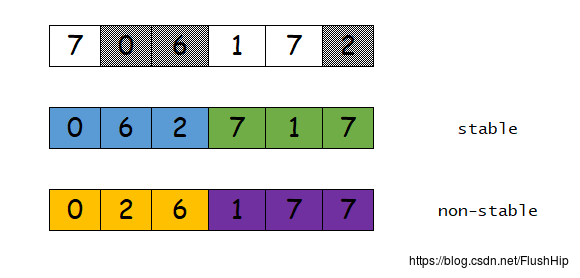
上面就是划分，把奇数和偶数划分开来，可以看到，statble_partition划分的时候可以保持序列之前的相对顺序，而partition就会破坏这种相对顺序。

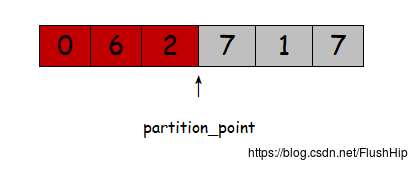
partition_point

C++11新增算法。这个算法会返回划分的界限，且这个算法针对已经划分好的元素有效，虽然说partition的返回值就是划分点，但是如果没有保存这个点，过一段之间后又想知道划分点，这个时候就只能遍历了，由于划分后的序列满足二分条件，因此partition_point就出来了。二分找到划分点。

Demo

void PartialDemo()
{
    std::vector res {2, 1, 0, 3, 3, 5, 8};
    std::vector aux(res);

    std::cout << "{2, 1, 0, 3, 3, 5, 8} partition :" << std::endl;

    auto pre = std::partition(std::begin(aux), std::end(aux), [] (const int & ele)
    {
        return ele % 2;
    });

    auto now = std::partition_point(std::begin(aux), std::end(aux), [] (const int & ele)
    {
        return ele % 2;
    });

    assert(&*pre == &*now);
    std::cout << "\tpartition_point at index of " << now - std::begin(aux) << std::endl;

    std::cout << "\tnon-stable : {";
    for (auto it = aux.begin(); it != aux.end(); std::cout << *it <<
            std::array{", ", "}\n"}[it + 1 == aux.end()], ++it) {}

    aux.assign(std::begin(res), std::end(res));

    std::stable_partition(std::begin(aux), std::end(aux), [] (const int & ele)
    {
        return ele % 2;
    });

    std::cout << "\tstable : {";
    for (auto it = aux.begin(); it != aux.end(); std::cout << *it <<
            std::array{", ", "}\n"}[it + 1 == aux.end()], ++it) {}

    std::cout << "{2, 1, 0, 3, 3, 5, 8} is partitioned ? " << std::boolalpha <<
            std::is_partitioned(std::begin(res), std::end(res), [] (const int & ele)
    {
        return ele % 2;
    }) << std::endl;
}

排序操作

• sort
• stable_sort
• partial_sort / partial_sort_copy
• nth_element
• is_sorted(C++11)
• is_sorted_until(C++11)

这是STL最精髓的部分了。也是最有味的部分，牵扯到一些思想和排序算法。

partial_sort

对序列的前部分进行排序，调用这个算法完后，可以保证前半部分一定有序，后半部分就不知道了。

nth_element

这个算法保证第n个位置上的元素一定是有序的，然后以这个位置为界限，右边的每一个元素都大于左边的每一个元素。有没有感觉这和快排的思想很像，在快排中，最理想的状态就是序列分成相等的两半，右边的元素都大于左边的元素。

用nth_element来重写快排：

template
void QuickSortBySTLnth_element(Iterator first, Iterator last)
{
    if (first == last || std::next(first) == last)
        return ;
    std::prev(first);
    Iterator mid = first + (last - first) / 2;
    std::nth_element(first, mid, last);
    QuickSortBySTLnth_element(first, mid);
    QuickSortBySTLnth_element(mid, last);
}

以后面试要手写快排再也不用担心了。

is_sorted / is_sorted_until

这个可以参考下面的Demo和下面讲堆操作时讲到的is_heap / is_heap_until。

Demo

void SortDemo()
{
    std::vector res(9);
    std::iota(std::begin(res), std::end(res), 0);

    auto print = [&res] (const std::string & str)
    {
        std::cout << str << " : ";
        std::ostream_iterator oit(std::cout, " ");
        std::copy(std::begin(res), std::end(res), oit);
        std::cout << std::endl;
    };

    std::shuffle(std::begin(res), std::end(res), std::mt19937(std::random_device{}()));

    print("origin sequence");

    std::cout << std::boolalpha << "sequence sorted ? " <<
            std::is_sorted(std::begin(res), std::end(res)) << std::endl;

    std::vector other;
    auto end = std::is_sorted_until(std::begin(res), std::end(res));
    other.assign(std::begin(res), end);
    other.swap(res);

    print("max sorted sequence");

    other.swap(res);

    std::nth_element(std::begin(res), std::begin(res) + res.size() / 2, std::end(res));
    std::cout << "the mid element is : " << *(std::begin(res) + res.size() / 2) << std::endl;

    std::partial_sort(std::begin(res), std::begin(res) + res.size() / 2, std::end(res));
    print("after partial_sort");

    std::sort(std::begin(res), std::end(res));
    print("after sort:");

    // stable_sort similar sort, so omit
}

二分操作

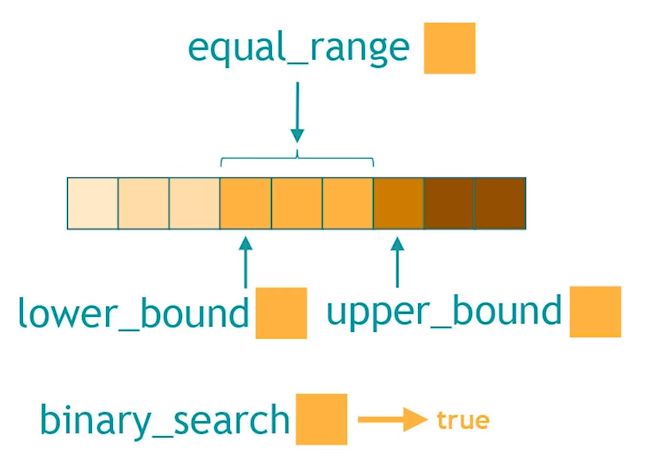
• lower_bound
• upper_bound
• binary_search
• equal_range

区间上的二分查找，很高效的算法。

Demo

这个可以参考今日头条2018校园招聘后端开发工程师(第二批)编程题 - 题解的第一题的代码。

合并操作

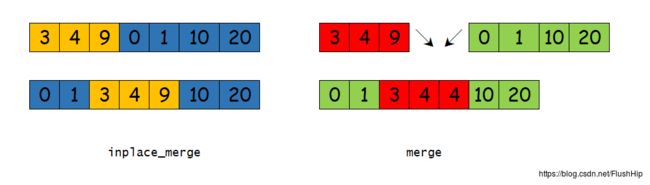
• merge
• inplace_merge

有序区间合并，而两者的区别就在于inplace_merge可以在就地进行(一个序列，前半部分和后部分分别有序)而不用借助额外的空间，而merge通常用来把不同有序序列合并，因此需要一个容器来放结果。

Demo

合并有序区间在归并排序用得挺多，因此用标准库的合并函数来重写下归并排序。

template
void MergeSortBySTLmerge(Iterator first, Iterator last)
{
    if (first == last || std::next(first) == last)
        return ;
    std::prev(first);
    Iterator mid = first + (last - first) / 2;
    MergeSortBySTLmerge(first, mid);
    MergeSortBySTLmerge(mid, last);
    std::vector tmp;
    std::merge(first, mid,
                mid, last,
                std::back_inserter(tmp));

    std::copy(std::begin(tmp), std::end(tmp), first);
}

template
void MergeSortBySTLinpalce_merge(Iterator first, Iterator last)
{
    if (first == last || std::next(first) == last)
        return ;
    std::prev(first);
    Iterator mid = first + (last - first) / 2;
    MergeSortBySTLmerge(first, mid);
    MergeSortBySTLmerge(mid, last);
    std::inplace_merge(first, mid, last);
}

可以看出，std::inpalce_merge在归并排序中还是好用。

比较操作

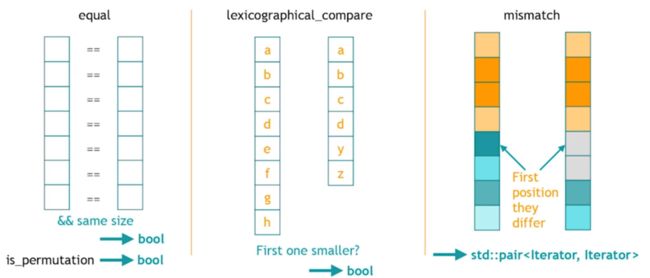
• equal
• lexicographical_compare
• mismatch

至少两个东西才能比较，因此，这三个算法操作的是两个序列，分别判断是否完全相同、字典序、第一个不同的地方。

Demo

注意equal和mismath这两个函数，接口的参数在C++不同版本不一样。C++14之前这两个函数默认认为两个序列的大小是相同的，因此只要传入3个参数就能正常工作。

void CompareDemo()
{
    std::vector A {6, 6, 7, 6, 6};
    std::vector B(A);

    std::cout <<
        std::boolalpha <<
        std::equal(std::begin(A), std::end(A),
                    std::begin(B)) <<
        std::endl;
#if __cplusplus >= 201402L
    std::cout <<
        std::boolalpha <<
        std::equal(std::begin(A), std::end(A),
                    std::begin(B), std::end(B)) <<
        std::endl;

#endif // __cplusplus

    std::cout <<
        std::boolalpha <<
        std::equal(std::begin(A), std::begin(A) + A.size() / 2,
                    A.rbegin()) <<
        std::endl;

    ++B[1];
    std::cout <<
        std::boolalpha <<
        std::lexicographical_compare(std::begin(A), std::end(A),
                                        std::begin(B), std::end(B)) <<
        std::endl;

    typedef std::vector::iterator Iter;
#if __cplusplus < 201402L
    std::pair p = std::mismatch(std::begin(A), std::end(B),
                                                std::begin(B));
#else
    std::pair p = std::mismatch(std::begin(A), std::end(B),
                                                std::begin(B), std::end(B));
#endif
    std::cout <<
        std::boolalpha <<
        "A : " << *p.first << " diff B : " << *p.second <<
        std::endl;
}

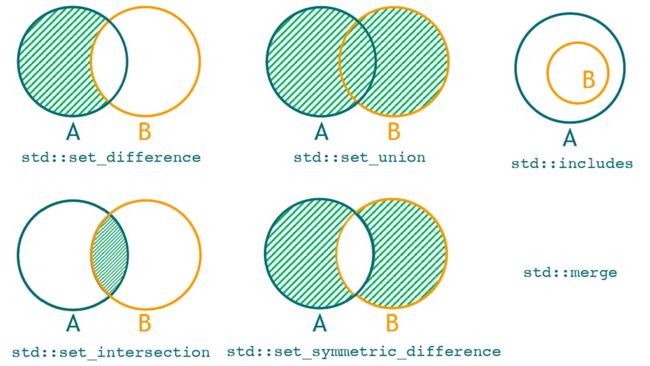
集合操作

STL把两个有序序列看成两个集合，然后这两个的”集合“可以进行如下的运算(交、并、补、查等等)，看看图就明白了。

• set_difference
• set_union
• set_intersection
• set_symmetric_differences
• includes
• merge

Demo

void AlgoSetDemo()
{
    std::vector A {2, 1, 3, 4, 5};
    std::vector B {4, 2, 10};
    std::vector result;

    auto print = [&result] (const std::string & str)
    {
        std::cout << str << " : ";
        for (auto it = result.begin(); it != result.end(); ++it)
            std::cout << *it << " \n"[std::next(it) == result.end()];
    };

    std::sort(std::begin(A), std::end(A));
    std::sort(std::begin(B), std::end(B));
    // A : 1 2 3 4 5
    // B : 2 4 10

    std::set_difference(std::begin(A), std::end(A),
                        std::begin(B), std::end(B),
                        std::back_inserter(result));
    print("set_difference");
    result.clear();

    std::set_union(std::begin(A), std::end(A),
                        std::begin(B), std::end(B),
                        std::back_inserter(result));
    print("set_union");
    result.clear();

    std::set_intersection(std::begin(A), std::end(A),
                        std::begin(B), std::end(B),
                        std::back_inserter(result));
    print("set_intersection");
    result.clear();

    std::set_symmetric_difference(std::begin(A), std::end(A),
                        std::begin(B), std::end(B),
                        std::back_inserter(result));
    print("set_symmetric_difference");
    result.clear();

    std::cout << std::boolalpha << "includes : " << std::includes(std::begin(A), std::end(A),
                                                                std::begin(B), std::end(B)) << std::endl;

    std::merge(std::begin(A), std::end(A),
                        std::begin(B), std::end(B),
                        std::back_inserter(result));
    print("merge");
}

堆操作

• make_heap
• push_heap
• pop_heap
• sort_heap
• is_heap(C++11)
• is_heap_until(C++11)

堆操作，建堆、向堆中压入一个元素、从堆中弹出一个元素、堆排序。这是堆的基本操作，而普通的堆是完全二叉树，可以用数组来存储，因此，C++标准库的堆操作，操作的是序列。

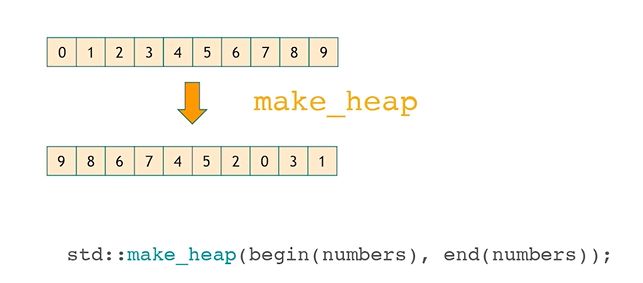
make_heap

把一串序列调整成最大堆的数组形式。

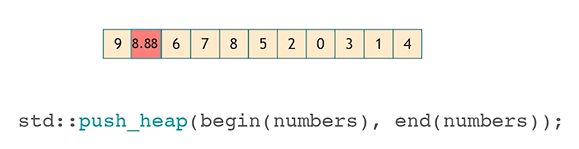
push_heap

先把一个元素加入序列。

然后对整个序列执行push_heap调整堆。

pop_heap

把堆顶元素和序列尾元素交换一下，调整堆就行了。

sort_heap

明白了上面pop_heap的过程，就会发现，pop_heap不会把序列尾的元素弹出序列，因此，利用这一定可以实现堆排序，堆排序是层有序的，也就是说最大的元素在堆顶，第二大的元素在第二层，依次类推。

template
void HeapSortBypop_heap(Iterator first, Iterator last)
{
    for (; first != last; std::pop_heap(first, last--)) {}
}

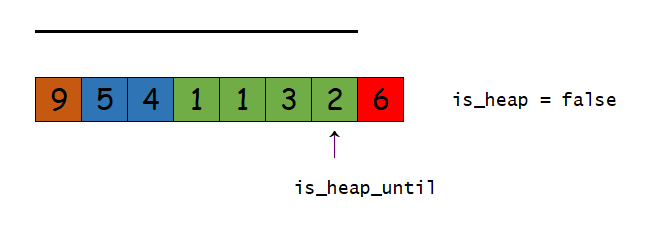
is_heap / is_heap_until

这是C++11的两个算法，功能是判断序列是否为最大堆以及在序列中找到一个最大的最大堆(以序列头为堆顶)。

Demo

void HeapDemo()
{
    std::vector result(8);
    std::iota(std::begin(result), std::end(result), 1);

    auto print = [] (const std::string & str, const int & ele)
    {
        std::cout << str << " : " << ele << std::endl;
    };

    std::for_each(std::begin(result), std::end(result), std::bind(print, "origin", std::placeholders::_1));
    std::cout << std::endl;

    std::make_heap(std::begin(result), std::end(result));

    std::for_each(std::begin(result), std::end(result), std::bind(print, "make_heap", std::placeholders::_1));
    std::cout << std::endl;

    result.push_back(100);
    std::push_heap(std::begin(result), std::end(result));

    std::for_each(std::begin(result), std::end(result), std::bind(print, "push_heap", std::placeholders::_1));
    std::cout << std::endl;

    std::pop_heap(std::begin(result), std::end(result));
    result.pop_back();

    std::for_each(std::begin(result), std::end(result), std::bind(print, "pop_heap", std::placeholders::_1));
    std::cout << std::endl;

    result[6] += 100;

    std::cout <<
            std::boolalpha << "is_heap : " <<
            std::is_heap(std::begin(result), std::end(result)) <<
            std::endl <<
            std::endl;

    std::for_each(std::begin(result),
                    std::is_heap_until(std::begin(result), std::end(result)),
                    std::bind(print, "is_heap_until", std::placeholders::_1));
    std::cout << std::endl;

    result[6] -= 100;

    std::sort_heap(std::begin(result), std::end(result));

    std::for_each(std::begin(result), std::end(result), std::bind(print, "sort_heap", std::placeholders::_1));
    std::cout << std::endl;
}

最大最小操作

• min_element / max_element / min_max_element
• min/ max / minmax
• clamp(C++17)

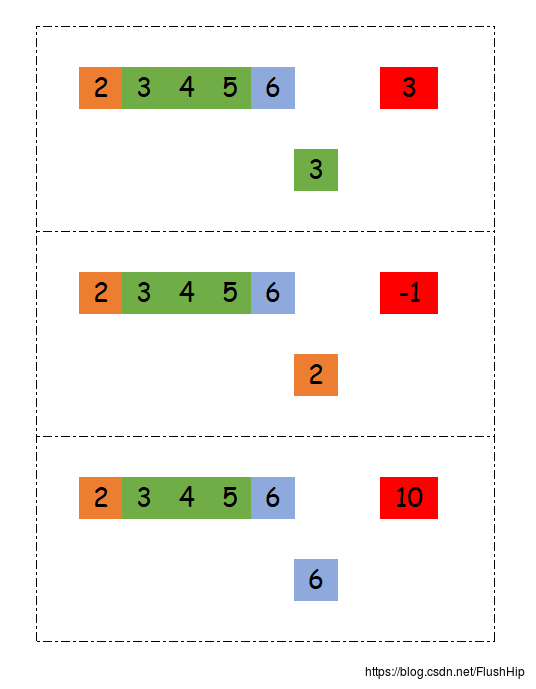
这应该是最不用说的算法了，min_element返回序列中最小值的位置。min返回两者较小的那个值。不过值得一提的是，min在C++11中可以求多个值中的最小值，这个得益于std::initializer_list的出现，这个在Demo中可以看到；

C++17的clamp算法挺好玩的，给定一个区间，一个元素，它返回这个区间最靠近这个元素的值。

Demo

void MinMaxDemo()
{
    std::initializer_list list = {3, -1, 8, 9, 2};
    std::vector result(list);

    std::cout << "max_element : " << *std::max_element(std::begin(result), std::end(result)) << std::endl;
    std::cout << "min_element : " << *std::min_element(std::begin(result), std::end(result)) << std::endl;

    typedef std::vector::iterator Iter;
    std::pair pairIter = std::minmax_element(std::begin(result), std::end(result));
    std::cout << "minmax_element : min_" << *pairIter.first << " max_" << *pairIter.second << std::endl;

    std::cout << "min{list} : " << std::min(list) << std::endl;
    std::cout << "max{list} : " << std::max(list) << std::endl;
    std::cout << "min{3, -1, 8, 9, 2} : " << std::min({3, -1, 8, 9, 2}) << std::endl;
    std::cout << "max{3, -1, 8, 9, 2} : " << std::max({3, -1, 8, 9, 2}) << std::endl;

    std::pair pairInt = std::minmax({3, -1, 8, 9, 2});
    std::cout << "minmax{3, -1, 8, 9, 2} : min_" << pairInt.first << " max_" << pairInt.second << std::endl;

    std::cout << __cplusplus << std::endl;
#if __cplusplus >= 201703L
    int left = 3, right = 8, tag = 5;
    std::cout << "tag_" << tag << " in clamp(" << left << ", " << right << ") : " <<
                std::clamp(tag, left, right) << std::endl;
    tag = -1;
    std::cout << "tag_" << tag << " in clamp(" << left << ", " << right << ") : " <<
                std::clamp(tag, left, right) << std::endl;

    tag = 10;
    std::cout << "tag_" << tag << " in clamp(" << left << ", " << right << ") : " <<
                std::clamp(tag, left, right) << std::endl;
#endif // __cplusplus
}

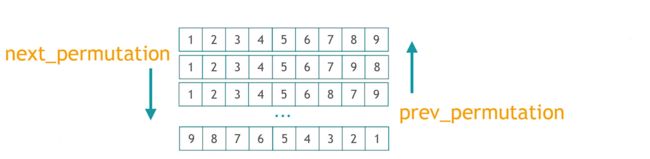
排列操作

• next_permutation
• prev_permutation
• is_permutation(C++11)

Demo

C++标准库中的全排列算法。最经典的问题就是判断两个序列是否互为全排列。

最好的做法就是把两个序列排序，然后判断是否完全一样。

这里我们用next_permutation和is_permutation来做一下。

void PermutationDemo()
{
    std::vector A {1, 2, 3, 5, 4};
    std::vector B {2, 1, 5, 3, 4};

    std::vector AA(A), BB(B);

    std::sort(std::begin(AA), std::end(AA));
    std::sort(std::begin(BB), std::end(BB));

    std::cout << std::boolalpha <<
            "{1, 2, 3, 5, 4} is a permutation of {2, 1, 5, 3, 4} ? " <<
            std::equal(std::begin(AA), std::end(AA),
                                std::begin(BB)) <<
            std::endl;

    AA.assign(std::begin(A), std::end(A));
    BB.assign(std::begin(B), std::end(B));

    if (!std::lexicographical_compare(std::begin(AA), std::end(AA),
                                        std::begin(BB), std::end(BB)))
    {
        std::swap_ranges(std::begin(AA), std::end(AA),
                            std::begin(BB));
    }

    bool ans = false;
    do {
        ans = std::equal(std::begin(AA), std::end(AA),
                            std::begin(BB));
    } while (!ans && std::next_permutation(std::begin(AA), std::end(AA)));

    std::cout << std::boolalpha <<
            "{1, 2, 3, 5, 4} is a permutation of {2, 1, 5, 3, 4} ? " <<
            ans <<
            std::endl;

    std::cout << std::boolalpha <<
            "{1, 2, 3, 5, 4} is a permutation of {2, 1, 5, 3, 4} ? " <<
            std::is_permutation(std::begin(A), std::end(A),
                                std::begin(B)) <<
            std::endl;
}

数值操作

这类算法一般是对区间求值。C++98就只有前面的四个，到了C++11多了std::iota，C++17就多了一倍多的数值算法。

关于每个算法的职能还是看图清晰些，图中没有表现的，我再用文字描述。

• accumulate
• partial_sum
• inner_product
• adjacent_difference
• reduce(这个以及下面都是C++17的内容)
• transform_reduce
• inclusive_scan
• exclusive_scan
• transform_inclusive_scan
• transform_exclusive_scan
• gcd
• lcm

C++98

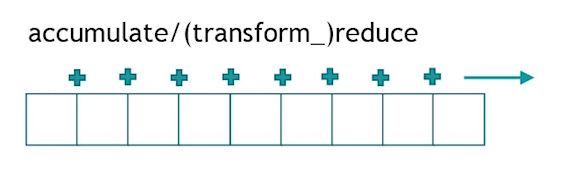
accumulate

不加可调用对象，默认就是对区间求和。

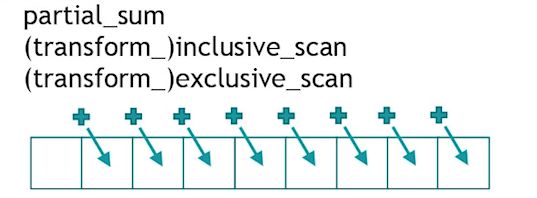
partial_sum

求前缀和，生成前缀和序列。

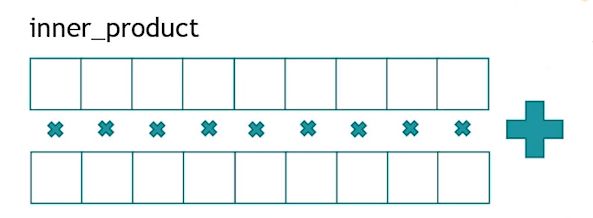
inner_product

类似向量求模。看图

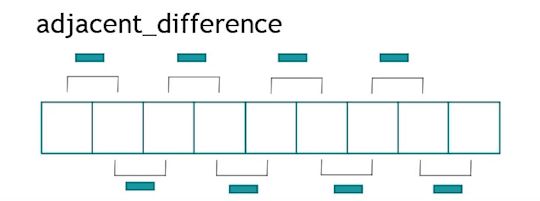
adjacent_difference

生成差值序列。

C++17

gcd、lcm

最大公约数，最小公倍数，C++17前，标准库有一个内部函数__gcd可以实现gcd功能，所以以前求最大公约数都是这么写的#define __gcd gcd。

下面这两个内容也牵扯到C++17的新东西，这里也不细说，后续会有博客继续讲。

reduce

(inclusive/exclusive)_scan

Demo

void NumericDemo()
{
    std::vector res {1, 2, 3, 4, 5}, aux;

    std::ostream_iterator osIter(std::cout, " ");

    std::cout << "{ ";
    std::copy(std::begin(res), std::end(res), osIter);
    std::cout << "} :\n";

    std::cout << "sum : " << std::accumulate(std::begin(res), std::end(res), 0) << std::endl;
    std::cout << "inner_product : " << std::inner_product(std::begin(res), std::end(res), std::begin(res), 0) << std::endl;

    std::partial_sum(std::begin(res), std::end(res), std::back_inserter(aux));

    std::cout << "partial_sum : ";
    std::copy(std::begin(res), std::end(res), osIter);
    std::cout << std::endl;

    aux.clear();

    std::adjacent_difference(std::begin(res), std::end(res), std::back_inserter(aux));

    std::cout << "adjacent_difference : ";
    std::copy(std::begin(res), std::end(res), osIter);
    std::cout << std::endl;

    int m = 6, n = 4;

    int g =
#if __cplusplus >= 201702L
        std::gcd(m, n);
#else
        std::__gcd(m, n);
#endif // __cplusplus

    int l =
#if __cplusplus >= 201702L
        std::lcm(m, n);
#else
        m * n / g;
#endif // __cplusplus
    std::cout << "6 and 4 the gcd is " << g << " , the lcm is " << l << std::endl;
}

未初始化内存上的操作

• uninitialized_copy
• uninitialized_copy_n(C++11)
• uninitialized_fill / uninitialized_fill_n
• uninitialized_move / uninitialized_move_n(这个及以下都是C++17的算法)
• uninitialized_default_construct / uninitialized_default_construct_n
• uninitialized_value_construct / uninitialized_value_construct_n
• destroy / destroy_at / destroy_n

在这张图可以看到，调用uninitialized_*前缀的函数都是调用构造函数。

这个配合源码讲会更好，这里不做过多深入，以后会有博客。

总结

• 凡是STL算法库中你认为操作两个序列，这两个序列应该具有相同长度，那么在C++11以及以前的接口中，只需要3个参数，它默认序列相同，而在C++14以后，不默认序列长度相同，因此需要4个参数
• 想到再写吧。

---

参考：

• FluentCpp - 105 STL Algorithms in Less Than an Hour
• C++ Standard Libarary Algorithm Hearder
• [FluentCpp - The World Map of C++ STL Algorithms](https://www.fluentcpp.com/getthemap/
• 算法库参考手册
• 候捷《STL源码剖析》