K-近邻算法原理介绍以及kd树实现K-近邻算法

K-近邻算法原理介绍以及kd树实现K-近邻算法

K近邻算法是一种常用的有监督的机器学习方法，k-近邻算法也被称为KNN算法，它可以解决分类问题，也可以解决回归问题。本文的主要内容如下：

l KNN算法的原理以及优缺点

l KNN算法的三个基本要素

l KNN算法的基本实现步骤

l kd树以及kd树实现k-近邻算法

1. KNN算法的原理

KNN算法的工作原理非常简单：给定一个训练数据集，对新的输入实例，在训练集中找到与该实例最邻近的K个实例（也就是k个邻居），这k个实例的多数属于某个类，就把该输入实例分类到这个类中。

举例说明：

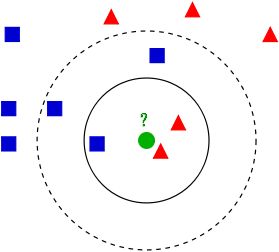
如上图所示，有两类不同的样本数据，分别用蓝色的小正方形和红色的小三角形表示，而图正中间的那个绿色的圆所标示的数据则是待分类的数据。

问题：给这个绿色的圆分类？

如果k=3，绿色圆点的最近的3个邻居是2个红色小三角形和1个蓝色小正方形，少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于红色的三角形一类。

如果k=5，绿色圆点的最近的5个邻居是2个红色三角形和3个蓝色的正方形，还是少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于蓝色的正方形一类。

1.1 KNN算法的优缺点

l 优点：

1. 简单，易于理解，无需建模与训练，易于实现；

2. 适合对稀有事件进行分类；

3. 适合与多分类问题，例如根据基因特征来判断其功能分类，KNN比SVM的表现要好。

l 缺点：

1. 惰性算法，内存开销大，对测试样本分类时计算量大，性能较低；

2. 可解释性差，无法给出决策树那样的规则。

2.KNN算法的三个基本要素

2.1 k值的选择

k 值的选择会对算法的结果产生重大影响。k值较小意味着只有与输入实例较近的训练实例才会对预测结果起作用，但容易发生过拟合；如果 k 值较大，优点是可以减少学习的估计误差，但缺点是学习的近似误差增大，这时与输入实例较远的训练实例也会对预测起作用，使预测发生错误。具体应用中k值的选择需要通过大量的实验来选择。

2.2 距离度量

K近邻算法的核心在于找k个最近的邻居，为什么要找距离最近的k个邻居，那是因为在特征空间中两个实例点的距离可以反应出两个实例点的相似程度，而K近邻模型的特征空间一般是n维实数向量空间，可以使用欧式距离测量两个实例间的距离，也课使用其它距离公式测量，如曼哈顿距离、切比雪夫距离、闵可夫斯基距离（Minkowski Distance）。

2.2.1 欧式距离

最常见的两点之间或多点之间的距离表示法，又称之为欧几里得度量，它定义于欧几里得空间中，如点 和 之间的距离为：

2.2.2 曼哈顿距离

我们可以定义曼哈顿距离的正式意义为L1-距离或城市区块距离，也就是在欧几里得空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。例如在平面上，坐标的点P1与坐标的点P2的曼哈顿距离为：，要注意的是，曼哈顿距离依赖座标系统的转度，而非系统在座标轴上的平移或映射。

通俗来讲，想象你在曼哈顿要从一个十字路口开车到另外一个十字路口，驾驶距离是两点间的直线距离吗？显然不是，除非你能穿越大楼。而实际驾驶距离就是这个“曼哈顿距离”，此即曼哈顿距离名称的来源， 同时，曼哈顿距离也称为城市街区距离(City Block distance)。

2.2.3 切比雪夫距离

切比雪夫距离（Chebyshev distance），二个点之间的距离定义为其各坐标数值差的最大值。点P1 和P2 的距离如下：

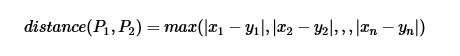
2.2.4 闵可夫斯基距离（Minkowski Distance）

闵尔科夫斯基距离（闵式距离），以俄国科学家闵尔科夫斯基命名，是欧氏距离的推广，是一组距离的的定义。点P1 和P2 的距离如下：

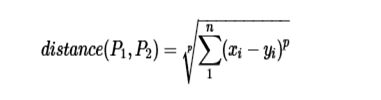
当p=1时，就是曼哈顿距离；

当p=2时，就是欧式距离；

当p→∞时，就是切比雪夫距离；

根据参数的不同，闵氏距离可以表示一类的距离。

2.3 分类决策规则

往往是多数表决，即由输入实例的 K 个最临近的训练实例中的多数类决定输入实例的类别。

3. KNN算法的基本实现步骤

算法基本步骤：

1）计算待分类点与已知类别的点之间的距离

2）按照距离递增次序排序

3）选取与待分类点距离最小的k个点

4）确定前k个点所在类别的出现次数

5）返回前k个点出现次数最高的类别作为待分类点的预测分类

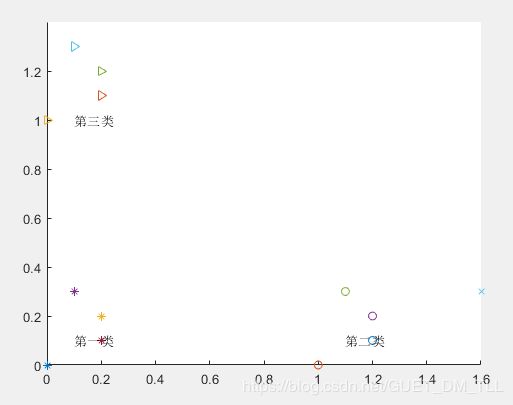
下面是一个按照算法基本步骤用matlab实现的简单例子，根据已分类的9个样本点来预测未知点（如图蓝色x点（1.6，0.3））的分类：

%实现KNN算法

%%算法描述

%1、初始化训练集和类别；

%2、计算测试集样本与训练集样本的欧氏距离；

%3、根据欧氏距离大小对训练集样本进行升序排序；

%4、选取欧式距离最小的前K个训练样本，统计其在各类别中的频率；

%5、返回频率最大的类别，即测试集样本属于该类别。

clear all

clc

%%算法实现

%step1、初始化训练集、测试集、K值

%创建一个三维矩阵，二维表示同一类下的二维坐标点，第三维表示类别

trainData1=[0 0;0.1 0.3;0.2 0.1;0.2 0.2]; %第一类训练集

trainData2=[1 0;1.1 0.3;1.2 0.1;1.2 0.2];%第二类训练集

trainData3=[0 1;0.1 1.3;0.2 1.1;0.2 1.2]; %第三类训练集

trainData(:,:,1)=trainData1;%设置第一类测试数据

trainData(:,:,2)=trainData2;%设置第二类测试数据

trainData(:,:,3)=trainData1;%设置第三类测试数据

trainDim=size(trainData);%获取训练集的维数

testData=[1.6 0.3];%设置1个测试点

k=7;
%%分别计算测试集中各个点与每个训练集中的点的欧氏距离

%把测试点扩展成矩阵

testData_rep=repmat(testData,4,1);

%设置三个二维矩阵存放测试集与测试点的扩展矩阵的差值平方

%diff1=zero(trainDim(1),trianDim(2));

%diff2=zero(trainDim(1),trianDim(2));

%diff3=zero(trainDim(1),trianDim(2));

for i=1:trainDim(3)

diff1=(trainData(:,:,1)-testData_rep).^2;

diff2=(trainData(:,:,2)-testData_rep).^2;

diff3=(trainData(:,:,3)-testData_rep).^2;

end

%设置三个一维数组存放欧式距离

distance1=(diff1(:,1)+diff1(:,2)).^2;

distance2=(diff2(:,1)+diff2(:,2)).^2;

distance3=(diff3(:,1)+diff3(:,2)).^2;

%将三个一维数组合成一个二维矩阵

temp=[distance1 distance2 distance3];

%将这个二维矩阵转换为一维数组

distance=reshape(temp,1,3*4);

%对距离进行排序

distance_sort=sort(distance);

%用一个循环寻找最小的K个距离里面那个类里出现的频率最高，并返回该类

num1=0;%第一类出现的次数

num2=0;%第二类出现的次数

num3=0;%第三类出现的次数

sum=0;%sum1,sum2,sum3的和

for i=1:k

for j=1:4

    if distance1(j)==distance_sort(i)

        num1=num1+1;

    end

    if distance2(j)==distance_sort(i)

        num2=num2+1;

    end

    if distance3(j)==distance_sort(i)

        num3=num3+1;

    end

end

sum=num1+num2+num3;

if sum>=k

    break;

end

end

class=[num1 num2 num3];

classname=find(class(1,:)==max(class));

fprintf(‘测试点（%f %f）属于第%d类’,testData(1),testData(2),classname);

%%使用绘图将训练集点和测试集点绘画出来

figure(1);

hold on;

for i=1:4

plot(trainData1(i,1),trainData1(i,2),'*');

plot(trainData2(i,1),trainData2(i,2),'o');

plot(trainData3(i,1),trainData3(i,2),'>');

end

plot(testData(1),testData(2),‘x’);

text(0.1,0.1,‘第一类’);

text(1.1,0.1,‘第二类’);

text(0.1,1,‘第三类’);

结果如下：

4. kd树以及kd树实现k-近邻算法

4.1 kd树

实现k近邻算法时，主要考虑的问题是如何对训练数据进行快速k近邻搜索。这在特征空间的维数大及训练数据容量大时尤其必要。k近邻算法最简单的实现是线性扫描（穷举搜索），即要计算输入实例与每一个训练实例的距离。计算并存储好以后，再查找K近邻。当训练集很大时，计算非常耗时。为了提高kNN搜索的效率，可以考虑使用特殊的结构存储训练数据，以减小计算距离的次数。

kd树(K-dimension tree)是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。kd树是一种二叉树，表示对k维空间的一个划分，构造kd树相当于不断地用垂直于坐标轴的超平面将K维空间切分，构成一系列的K维超矩形区域。kd树的每个结点对应于一个k维超矩形区域。利用kd树可以省去对大部分数据点的搜索，从而减少搜索的计算量。

4.2 构造kd树

输入：k维空间数据集，其中，

输出：kd树

（1）开始：构造根节点，根节点对应于包含T的k维空间的超巨星区域。选择为坐标轴，以T中所有实例的坐标的中位数为切分点，将根节点对应的超矩形区域划分为两个子区域。切分由通过切分点并与坐标轴垂直的超平面实现。由根节点生成深度为1的左、右子节点：左子节点对应坐标小于切分点的子区域，右子节点对应坐标大于切分点的子区域。将落在切分超平面上的实例点保存在根节点。

（2）重复：对深度为j的节点，选择为切分的坐标轴，l=j%k+1,以该节点的区域中所有实例的坐标的中位数为切分点，将该节点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴垂直的超平面实现。由该节点生成深度为j+1的左、右子节点：左子节点对应坐标小于切分点的子区域，右子节点对应坐标大于切分点的子区域。将落在切分超平面上的实例点保存在根节点。

下面用一个简单的2维平面上的例子来进行说明。

例. 给定一个二维空间数据集：T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)} T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)} ，构造一个平衡kd树。

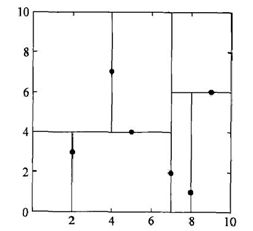
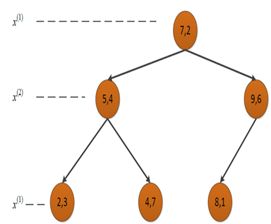
解：根结点对应包含数据集T的矩形，选择轴，6个数据点的 坐标中位数是6，这里选最接近的(7,2)点，以平面 =7将空间分为左、右两个子矩形（子结点）；接着左矩形以=4 分为两个子矩形（左矩形中{(2,3),(5,4),(4,7)}点的坐标中位数正好为4，右矩形以=6 分为两个子矩形，如此递归，最后得到如下图所示的特征空间划分和kd树。

4.3 搜索kd树

利用kd树可以省去对大部分数据点的搜索，从而减少搜索的计算量。下面以搜索最近邻点为例加以叙述：给定一个目标点，搜索其最近邻，首先找到包含目标点的叶节点；然后从该叶结点出发，依次回退到父结点；不断查找与目标点最近邻的结点，当确定不可能存在更近的结点时终止。这样搜索就被限制在空间的局部区域上，效率大为提高。包含目标点的叶结点对应包含目标点的最小超矩形区域。以此叶结点的实例点作为当前最近点。目标点的最近邻一定在以目标点为中心并通过当前最近点的超球体内部。然后返回当前结点的父结点，如果父结点的另一子结点的超矩形区域与超球体相交，那么在相交的区域内寻找与目标点更近的实例点。如果存在这样的点，将此点作为新的当前最近点。算法转到更上一级的父结点，继续上述过程。如果父结点的另一子结点的超矩形区域与超球体不相交，或不存在比当前最近点更近的点，则停止搜索。

例：给定一个如下图所示的kd树，根结点为A，其子结点为B,C等。树上共存储7个实例点；另有一个输入目标实例点S，求S的最近邻。

解：首先在kd树中找到包含S的叶结点D，以点D作为近似最邻。真正最近邻一定在以点S为中心通过点D的圆的内部。然后返回结点D的父结点B，在结点B的另一子结点F的区域内搜索最近邻。结点F的区域与圆不相交，不可能有最近邻。继续返回上一级父结点A，在结点A的另一子结点C的区域内搜索最近邻。结点C的区域与圆相交；该区域在圆内的实例点有点E，点E比点D更近，成为新的最近邻近似。最后得到点E是点S的最近邻。

新的改变

我们对Markdown编辑器进行了一些功能拓展与语法支持，除了标准的Markdown编辑器功能，我们增加了如下几点新功能，帮助你用它写博客：

1. 全新的界面设计 ，将会带来全新的写作体验；
2. 在创作中心设置你喜爱的代码高亮样式，Markdown 将代码片显示选择的高亮样式 进行展示；
3. 增加了 图片拖拽 功能，你可以将本地的图片直接拖拽到编辑区域直接展示；
4. 全新的 KaTeX数学公式 语法；
5. 增加了支持甘特图的mermaid语法¹ 功能；
6. 增加了 多屏幕编辑 Markdown文章功能；
7. 增加了 焦点写作模式、预览模式、简洁写作模式、左右区域同步滚轮设置 等功能，功能按钮位于编辑区域与预览区域中间；
8. 增加了 检查列表 功能。

功能快捷键

撤销：Ctrl/Command + Z
重做：Ctrl/Command + Y
加粗：Ctrl/Command + B
斜体：Ctrl/Command + I
标题：Ctrl/Command + Shift + H
无序列表：Ctrl/Command + Shift + U
有序列表：Ctrl/Command + Shift + O
检查列表：Ctrl/Command + Shift + C
插入代码：Ctrl/Command + Shift + K
插入链接：Ctrl/Command + Shift + L
插入图片：Ctrl/Command + Shift + G
查找：Ctrl/Command + F
替换：Ctrl/Command + G

合理的创建标题，有助于目录的生成

直接输入1次#，并按下space后，将生成1级标题。
输入2次#，并按下space后，将生成2级标题。
以此类推，我们支持6级标题。有助于使用TOC语法后生成一个完美的目录。

如何改变文本的样式

强调文本 强调文本

加粗文本 加粗文本

标记文本

删除文本

引用文本

H₂O is是液体。

2¹⁰ 运算结果是 1024.

插入链接与图片

链接: link.

图片:

带尺寸的图片:

居中的图片:

居中并且带尺寸的图片:

当然，我们为了让用户更加便捷，我们增加了图片拖拽功能。

如何插入一段漂亮的代码片

去博客设置页面，选择一款你喜欢的代码片高亮样式，下面展示同样高亮的 代码片.

// An highlighted block
var foo = 'bar';

生成一个适合你的列表

• 项目
  • 项目
    • 项目

1. 项目1
2. 项目2
3. 项目3

• 计划任务
• 完成任务

创建一个表格

一个简单的表格是这么创建的：

项目	Value
电脑	$1600
手机	$12
导管	$1

设定内容居中、居左、居右

使用:---------:居中
使用:----------居左
使用----------:居右

第一列	第二列	第三列
第一列文本居中	第二列文本居右	第三列文本居左

SmartyPants

SmartyPants将ASCII标点字符转换为“智能”印刷标点HTML实体。例如：

TYPE	ASCII	HTML
Single backticks	'Isn't this fun?'	‘Isn’t this fun?’
Quotes	"Isn't this fun?"	“Isn’t this fun?”
Dashes	-- is en-dash, --- is em-dash	– is en-dash, — is em-dash

创建一个自定义列表

Markdown

Text-to- HTML conversion tool

Authors

John

Luke

如何创建一个注脚

一个具有注脚的文本。²

注释也是必不可少的

Markdown将文本转换为 HTML。

KaTeX数学公式

您可以使用渲染LaTeX数学表达式 KaTeX:

Gamma公式展示 $\Gamma (n)=(n-1)!\forall n\in \mathbb{N}$ 是通过欧拉积分

$$\Gamma (z)={\int }_0^{\infty }{t}^{z-1}{e}^{-t}dt.$$

你可以找到更多关于的信息 LaTeX 数学表达式here.

新的甘特图功能，丰富你的文章

Mon 06 Mon 13 Mon 20 已完成 进行中 计划一 计划二 现有任务 Adding GANTT diagram functionality to mermaid

• 关于 甘特图 语法，参考 这儿,

UML 图表

可以使用UML图表进行渲染。 Mermaid. 例如下面产生的一个序列图：

张三 李四 王五 你好！李四, 最近怎么样? 你最近怎么样，王五？ 我很好，谢谢! 我很好，谢谢! 李四想了很长时间, 文字太长了 不适合放在一行. 打量着王五... 很好... 王五, 你怎么样? 张三 李四 王五

这将产生一个流程图。:

链接

长方形

圆

圆角长方形

菱形

• 关于 Mermaid 语法，参考 这儿,

FLowchart流程图

我们依旧会支持flowchart的流程图：

Created with Raphaël 2.2.0 开始 我的操作 确认？ 结束 yes no

• 关于 Flowchart流程图 语法，参考 这儿.

导出与导入

导出

如果你想尝试使用此编辑器, 你可以在此篇文章任意编辑。当你完成了一篇文章的写作, 在上方工具栏找到 文章导出 ，生成一个.md文件或者.html文件进行本地保存。

导入

如果你想加载一篇你写过的.md文件，在上方工具栏可以选择导入功能进行对应扩展名的文件导入，
继续你的创作。

---

1. mermaid语法说明 ↩︎

2. 注脚的解释 ↩︎