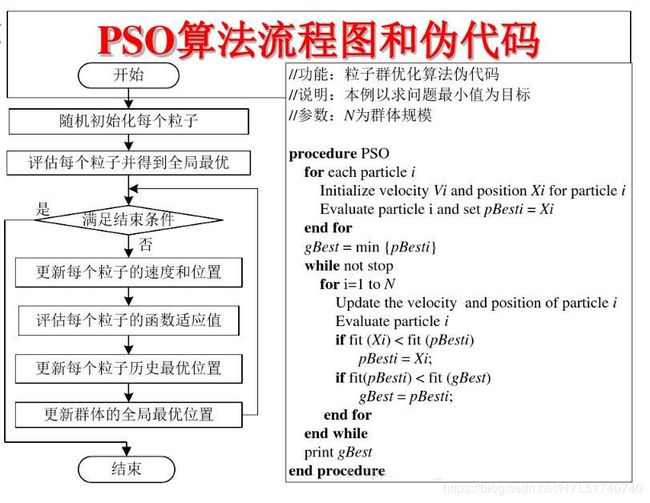
PSO(最详细的粒子群优化算法）详解（附带Java实现代码）

算法简介

起源

  粒子群优化算法(Particle Swarm Optimization，简称PSO)，是1995年Eberhart博士和Kennedy博士一起提出的，粒子群算法是通过模拟鸟群捕食行为设计的一种群智能算法。

简介

  区域内有大大小小不同的食物源，鸟群的任务是找到最大的食物源（全局最优解），鸟群的任务是找到这个食物源。鸟群在整个搜寻的过程中，通过相互传递各自位置的信息，让其他的鸟知道食物源的位置最终，整个鸟群都能聚集在食物源周围，即我们所说的找到了最优解，问题收敛。

特点

  通过群体中个体之间的协作和信息共享来寻找最优解，随着计算的推移，通过探索和利用搜索空间中已知的有利位置，粒子围绕一个或多个最优点聚集或聚合。该算法设计玄妙之处在于它保留了最优全局位置和粒子已知的最优位置两个信息。后续的实验发现，保留这两个信息对于较快收敛速度以及避免过早陷入局部最优解都具有较好的效果。这也奠定了后续粒子群算法改进方向的基础，算法目前已被广泛应用于函数优化、神经网络训练、模糊系统控制以及其他遗传算法的应用领域。

算法分析

基本思想

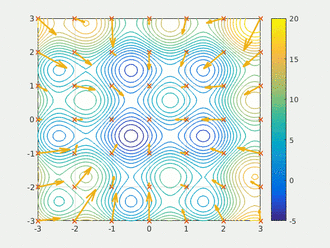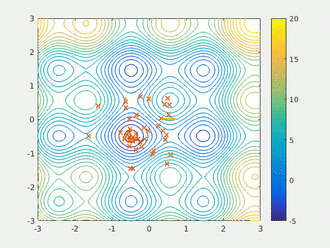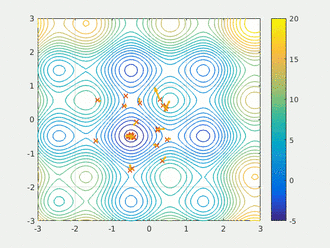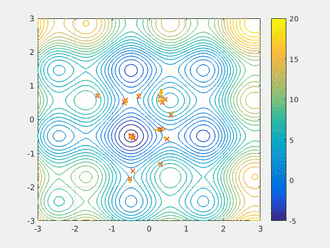
  鸟被抽象为没有质量和体积的微粒(点)，并延伸到$N$维空间，粒子$i$在$N$维空间的位置表示为矢量$X_i$=($X_1$，$X_2$，…，$X_n$)，飞行速度表示为矢量$V_i$＝($V_1$，$V_2$，…，$V_n$)。每个粒子都有一个由目标函数根据其位置来决定的适应值(Fitness Value)，并且知道自己到目前为止发现的最好位置$pbest$和现在的位置$X_i$（位置的好与坏取决于微粒的位置所对应的适应值），这个可以看作是粒子自己的飞行经验。除此之外，每个粒子还知道到目前为止整个群体中所有粒子发现的最好位置$gbest$（$gbest$是$pbest$中的最好值），这个可以看作是粒子同伴的经验。粒子就是通过自己的经验和同伴中最好的经验来决定下一步的运动。动图演示如下：

算法实现

基本步骤

• 初始化一群微粒
• 计算每个微粒的适应值并得到全局最优

• 对每个微粒，将其适应值与其经过的最好位置pbest的适应值作比较，如果较好，则将其作为当前的最好位置pbest
• 将每一个微粒最好位置所对应的适应值与所有微粒中最好位置gbest所对应的适应值进行比较，取所有微粒中最优适应值所对应的微粒位置作为当前全局的最好位置gbest

• 更新每一个微粒速度和位置
• 未达到结束条件则转第二步
• 

初始化

  首先，我们需要设置速度维度值最大值Vmax、最小值Vmin，位置维度值最大值Xmax、最小值Xmin，从而进行初始化时粒子速度和位置维度值。设置粒子种群规模Size以及空间维度N，使用如下公式对粒子的位置和速度进行初始化：

$$V_{i,j}=V_{min}+Random(0,1)\times (V_{max}-V_{min})$$

$$X_{i,j}=X_{min}+Random(0,1)\times (X_{max}-X_{min})$$

• $i\in [1,2,...,Size]$
• $j\in [1,2,...,N]$

计算每个微粒的适应值并得到全局最优

  我们根据每一个粒子的位置$X_i$计算其适应值，根据适应值是否最优优判断位置是否为历史最优，如果是，则更新粒子的历史最优位置，再根据对所有微粒的最优适应值的比较确定全局最优位置

更新每一个微粒速度和位置

  在每一次的迭代中，粒子通过跟踪两个“极值”($pbest$，$gbest$)来更新自己，在找到这两个最优值后，粒子通过下面的公式来更新自己的速度和位置：

$$V_{i,j}=\omega \times V_{i,j}+C_1\times Random(0,1)\times (pbes{t}_{i,j}-X_{i,j})-C_2\times Random(0,1)\times (gbes{t}_j-X_{i,j})$$

$$X_{i,j}=X_{i,j}+V_{i,j}$$

• $V_{i,j}$表示粒子$i$的速度矢量第$j$维的值
• $\omega$为惯性因子，调节解空间的搜索范围，通常为非负数

• 其值较大时，全局寻优能力强，局部寻优能力弱; 其值较小时，全局寻优能力弱，局部寻优能力强
• 动态$\omega$能获得比固定值更好的寻优结果，目前采用较多的是线性递减权值(Linearly Decreasing Weight，LDW)策略，也可以视具体问题而定

• $C_1$、$C_2$表示学习因子，用于调节学习的最大步长，范围[0,4]，通常取$C_1=C_2=2$
• $pbes{t}_{i,j}$是当前第$i$个粒子的最优适应值对应的位置的第$j$个维度的值
• $X_{i,j}$为当前粒子所在位置的第$j$维的值
• $gbes{t}_j$为集群中搜索到的最优适应值对应位置的第$j$维的值

判断是否满足终止条件

  如果不满足终止条件则返回至第二步，终止条件有多种，可以是直到达到最大运动的步数，或者达到所要求的收敛精度

代码实现（Java）

代码下载地址

https://download.csdn.net/download/HYL51740740/12416309

部分代码如下

import java.util.Random;

public class PSO1 {
    private static int M=200; //迭代次数

    private static int numParticles=50;    //粒子数
    private static int dimension=3;    //粒子维数

    private static double[][] pBest = new double[numParticles][dimension];  //存储各粒子的历史最优位置信息
    private static double[][] xPos = new double[numParticles][dimension];  //存储各粒子的当前位置信息
    private static double[][] xVel = new double[numParticles][dimension];  //存储各粒子的速度信息

    private static double[] gBest = new double[dimension];      //存储全局最优解对应的位置信息
    private static double[] fitness = new double[numParticles];    //存储各粒子适应值

    //相关参数
    private static double omega = 0.6;                 //惯性因子
    private static double c1 = 2.0;                       //学习因子
    private static double c2 = 2.0;
    private static double xMax = 10;                        // 空间中位置维度值和速度维度值的边界
    private  static  double xMin = -10;
    private static double vMax = 5;
    private static double vMin = -5;

    private Random random = new Random();

PSO算法与GA算法比较

共性

• 都属于仿生算法
• 都属于全局优化方法
• 都属于随机搜索算法
• 都隐含并行性
• 根据个体的适配信息进行搜索，因此不受函数约束条件的限制，如连续性、可导性等
• 对高维复杂问题，往往会遇到早熟收敛和收敛 性能差的缺点，都无法保证收敛到最优点

差异

• PSO有记忆，好的解的知识所有粒子都保 存，而GA（Genetic Algorithm），以前的知识随着种群的改变被改变。
• PSO中的粒子仅仅通过当前搜索到最优点进行共享信息，所以很大程度上这是一种单共享项信息机制。而GA中，染色体之间相互共享信息，使得整个种群都向最优区域移动。
• GA的编码技术和遗传操作比较简单，而PSO相对于GA，没有交叉和变异操作，粒子只是通过内部速度进行更新，因此原理更简单、参数更少、实现更容易。
• 应用于人工神经网络(ANN)，PSO的潜力较大

部分图片及文字资料来着论坛，笔记经过精心整理，如文中有错误欢迎提出