卷积神经网络原理
(文章同步更新在@dai98.github.io)
卷积神经网络 (Convolutional Neural Network, CNN)是受生物学上感受野机制的启发而提出的深度学习模型,在图像处理中较为常见,下面我们依次介绍各种层的结构和作用。
一、从图像到矩阵
每张图片都是由像素组成的,一张图片每行和每列有多少个像素即为图片的分辨率 (Resolution);每一个像素都有一个颜色,这个颜色是由三个属性组成的,分别为红、绿、蓝,我们把这三个属性叫做通道 (Channel)。当然,这是对于彩色图片来讲,对于黑白照片的而言,每个像素只有灰度一个属性。
一般来讲,每个通道的值在0到255之间。这样,一张分辨率为100x100的彩色照片就可以转换为一个(100,100,3)的张量;相同大小的黑白照片可以转换为(100,100,1)的张量。
二、前馈神经网络的缺陷
MNIST数据集是图像处理领域较为著名的数据集,由50000个0到9的手写数字组成,我们要对图像进行多分类,每张照片为28x28x1的灰度图片。
假设我们使用两层的前馈神经网络来解决该问题,隐藏层使用15个神经元,那我们需要计算 28 × 28 × 15 + 10 × 15 + 15 + 10 = 11 , 935 28\times 28\times 15 + 10 \times 15 + 15+10 = 11,935 28×28×15+10×15+15+10=11,935个参数,在反向传播的时候需要大量的计算。而我们知道图片分辨率为28x28已经非常小了,如今的照片的分辨率可以达到2000x3000,传统的前馈神经网络无法完成数量如此庞大的参数计算。
前馈网络的另一个缺陷是无法捕获到图片中的不变特征。一张图片进行放缩或旋转后,其中的特征保持不变,而前馈网络较难捕获到这些不变的特征。
而卷积神经网络用一种不同的结构,可以较好的解决上面的问题。下面我们来分别介绍一下卷积神经网络的主要部分:卷积层、池化层、全连接层。
三、数据输入层
该层要做的处理主要是对原始图像数据进行预处理,其中包括:
- 中心化:把输入数据各个维度都减去该维度的平均值,使其中心化为0
- 归一化:使数据的标准差为1
- PCA/白化:用PCA降维;白化是对数据各个特征轴上的幅度归一化
中心化与归一化示例:
去相关与白化示例:
四、卷积层
1. 卷积计算
二维的卷积计算在图像处理领域经常能够用到,卷积计算需要一个叫做卷积核 (Convolution Kernel)或者叫滤波器(Filter)的结构,实际上是一个矩阵。假设图片 X ∈ R M × N X\in\R^{M\times N} X∈RM×N,卷积核 w ∈ R m × n w\in\R^{m\times n} w∈Rm×n,且一般 m < < M , n < < N m<
y i j = ∑ u = 1 m ∑ v = 1 n w u v ⋅ x i − u + 1 , j − v + 1 y_{ij} = \sum_{u=1}^m\sum_{v=1}^n w_{uv}\cdot x_{i-u+1,j-v+1} yij=u=1∑mv=1∑nwuv⋅xi−u+1,j−v+1
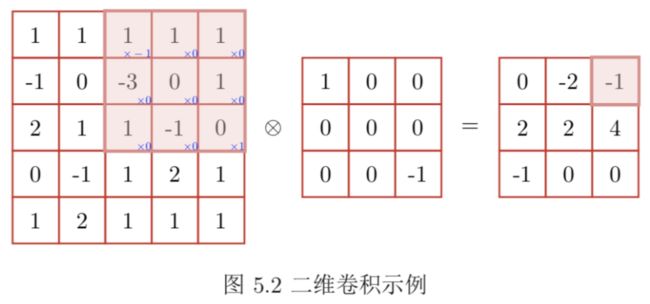
卷积实例如下图:
被卷积核扫描到的区域,依次和卷积核的翻转对应的数字相乘,再把所有结果求和。在该例中,即 1 × ( − 1 ) + 1 × 0 + 1 × 0 + ( − 3 ) × 0 + 0 × 0 + 1 × 0 + 1 × 0 − 1 × 0 + 0 × 1 = − 1 1\times (-1) + 1\times 0+ 1\times 0+ (-3)\times 0+ 0\times 0+ 1\times 0+ 1\times 0 - 1\times 0+ 0\times 1=-1 1×(−1)+1×0+1×0+(−3)×0+0×0+1×0+1×0−1×0+0×1=−1,并把最后的结果 − 1 -1 −1写在了结果对应的位置上。这是一次卷积的计算,而我们的卷积核需要依次扫描整个图片,来得到最后的结果,我们将其称之为特征映射 (Feature Map),如下图:
你或许会注意到,为什么上面计算卷积的时候 1 1 1和 − 1 -1 −1的位置交换了呢?这是因为在二维卷积的计算中,我们要先将卷积核进行翻转180°,再进行卷积运算;而在实际实现的时候,我们用相关性来代替卷积,相关性与卷积的区别只在于相互关在计算之前没有180°翻转卷积核,因此相关性也被称为不翻转卷积,或者干脆和卷积混为一谈。
在深度学习中,我们使用卷积层的目的是为了特征提取,卷积核是否翻转也不会影响模型的学习能力,特别是,卷积核也是学习的参数的时候,卷积与相互关是等价的。实际上,许多深度学习模型都是用相互关来代替卷积。
2. 卷积核的种类与超参数
那我们究竟该如何选择卷积核呢?实际上,经验告诉我们有许多种卷积核可供选择,不同种类的卷积核可以完成不同的任务:
卷积核还有三个超参数,即步长 (Stride)、零填充 (Zero Padding)与深度 (Depth)。步长是指窗口滑动的间隔,上面的例子都是步长等于1。零填充是在输入向量两端进行补零。深度是卷积核的数量,应该与下一层的神经元数量相同。
假设卷积层的输入神经元数量为 n n n,卷积大小为 m m m,步长为 s s s,输入神经元两层各补 p p p个0,那么卷积层的神经元数量为 n − m + 2 p s + 1 \frac{n-m+2p}{s} + 1 sn−m+2p+1。
一般的有三种常用的卷积:
- 窄卷积 (Narrow Convolution): 步长 s = 1 s=1 s=1,两端不补零 p = 0 p=0 p=0,卷积后输出长度为 n − m + 1 n-m+1 n−m+1
- 宽卷积 (Wide Convolution): 步长 s = 1 s=1 s=1,两端补零 p = m − 1 p=m-1 p=m−1,卷积后输出长度为 n + m − 1 n+m-1 n+m−1
- 等宽卷积 (Equal-Width Convolution): 步长 s = 1 s=1 s=1,两端补零 p = m − 1 2 p=\frac{m-1}{2} p=2m−1,卷积后输出长度为 n n n
3. 三维卷积核
卷积核不止有二维的,也有三维的卷积核,这时候卷积核的参数不知有高度和宽度,还有深度。二维的卷积核的参数为[channel, width, height],三维的卷积核的参数为[channel, width, height, depth]。
上面的图可以帮助我们理解。图a是指灰度图片,只有一个通道,卷积核的通道为1,卷积核输出的特征映射的通道为1,这是二维卷积;图b指的是彩色图片,有三个通道 (实际上图(b)显示的是有多个帧的情况,但为了便于理解,在这里我说成是通道,影响并不大),我们的卷积核的通道为3,因此特征映射的通道还是为1,这也是二维卷积;图c所对应的三位卷积,需要更多的信息,例如在该图中我们输入的是一段视频,卷积核的深度对应的是视频有多少帧 (视频实际上是连续播放的图片,若视频一秒播放 k k k张图片,我们称视频一秒有 k k k帧),在图中视频一共有 L L L帧,我们的卷积核的深度为 d d d帧,且 d < L d
不难发现,三维卷积通常需要更多的数据来支持三维卷积核的运算,对于一般的照片,二维卷积核便足够使用了。
4. 参数共享
我们假设每个卷积核在图片中的权重是固定的,进一步减少参数的数量。假设我们的输入是分辨率为32x32的彩色图片,有三个通道,因此图片的大小为(3,32,32),并有步长为1,零填充为2,有10个5x5的卷积核,那么我们特征映射的边长为:
32 + 2 × 2 − 5 1 + 1 = 32 \frac{32 + 2 \times 2 - 5}{1} + 1 = 32 132+2×2−5+1=32
若我们不参数共享,那我们需要 10 × 32 × 32 × 5 × 5 × 3 = 768 , 000 10\times 32\times 32\times 5\times 5\times 3 = 768,000 10×32×32×5×5×3=768,000个参数
若我们进行参数共享,那我们需要 10 × 5 × 5 × 3 = 750 10\times 5\times 5\times 3 = 750 10×5×5×3=750个参数
可以发现,参数共享使得我们的卷积核只能捕获一个很小的局部特征,如果图像很大的化就会导致特征的丢失,为了解决该问题,我们可以在每个卷积层中设置多个卷积核。
五、池化层
池化层(Pooling),也叫子采样层(Subsampling),是用来提取特征,以此减少神经元的数量,防止过拟合的出现。虽然卷积层在一定程度上减少了神经元数量,但如果此时我们直接连接全连接层进行分类,还是有很多的参数。池化层的思路也很简单,我们把卷积层得到的特征映射集中的每一个特征映射分成很多块,用某一种方式来计算出一个值,窗口再继续滑动,获取下一个块中的值;在统计学上,我们将其称之为下采样 (Down Sampling)。
如果换做更严谨的数学语言,就是我们通过卷积层获得了特征映射集 X ∈ R M × N × D X\in \R^{M\times N\times D} X∈RM×N×D,其中每一个特征映射为 X d X^d Xd,将其划分为很多区域 R m , n d R^d_{m,n} Rm,nd, 1 ≤ m ≤ M ′ 1\leq m \leq M' 1≤m≤M′, 1 ≤ n ≤ N ′ 1\leq n \leq N' 1≤n≤N′,分出的块 R d R^d Rd可以重叠,也可以不重叠,取决于窗口的步长。
对于分出的块 R m , n d R^d_{m,n} Rm,nd,我们通过池化函数 (Pooling Function)来获得一个新值,最常用的池化函数有两种,分别为最大池化(Maximum Pooling)与平均池化(Average Pooling)。
- 最大池化
最大池化是取一个区域内所有神经元的最大值,即
Y m , n d = m a x x i , i ∈ R m , n d Y_{m,n}^d=max\ x_i,\ i\in R^d_{m,n} Ym,nd=max xi, i∈Rm,nd
其中 x i x_i xi是 R m , n d R^d_{m,n} Rm,nd上每个神经元的激活值。 - 平均池化
平均池化与最大池化的思路很相似,只不过这次我们获得的值是 R m , n d R^d_{m,n} Rm,nd上所有神经元激活值的平均值 ,即
Y m , n = 1 ∣ R m , n d ∣ ∑ i ∈ R m , n d x i Y_{m,n}=\frac{1}{|R^d_{m,n}|}\sum_{i\in R_{m,n}^d}x_i Ym,n=∣Rm,nd∣1i∈Rm,nd∑xi
上图即是最大池化,我们可以看到,随着2x2的滤波器,且步长为2,我们4x4的矩阵下采样为2x2的矩阵,参数进一步降低了。你可以从图中看到,不同的颜色是特征映射上不同的块,且每个块最终取的为最大值。若为平均池化,我们最终得到的是每个块中元素的值的平均数。
六、Flatten层与全连接层
Flatten层的目的是将高维数据压缩为向量,以便之后的全连接层进行分类。Flatten层一般在池化层之后,在全连接层之前,不会影响batch的大小。
一般全连接层为卷积神经网络的最后一层,与前馈神经网络的层无区别,通过不同的激活函数来进行二分类或是多分类任务。
七、卷积神经网络的结构
现在我们就可以将上面介绍的层拼装起来,组成一个卷积神经网络。上面的图为1994年解决手写字体分类的模型LeNet5,每个卷积层后都用ReLU激活函数,之后连接池化层,最后经过两个全连接层给出预测。
八、参考资料
[1]. 第五章 卷积神经网络
[2]. 深度理解卷积神经网络
[3]. 卷积神经网络和TextCNN
[4]. 《动手学深度学习》
[5]. 卷积神经网络的直观解释
[6]. 卷积神经网络CNN原理详解
[7]. 知乎:CNN中卷积层的计算细节
[8]. 卷积、卷积核的维数、尺寸
[9]. CNN两大神器:局部感知、参数共享
[10]. CNN中的局部连接与权值共享
[11]. CNN中的权值共享理解
[12]. 知乎 - 卷积神经网络中二维卷积核与三维卷积核有什么区别?
[13]. 卷积神经网络CNN总结
[14]. 卷积参数共享机制
[15]. 一张图理解卷积神经网络卷积层和感受野