拉格朗日函数与广义拉格朗日函数

拉格朗日函数用来求解等式约束的最优化问题；广义拉格朗日函数用来求解不等式约束的最优化问题。

无约束优化问题

关于优化问题包括无约束优化问题，等式约束优化问题，不等式约束优化问题。这里简略地介绍一下无约束优化问题。（以后再来填坑。）
考虑无约束优化问题：
$$\underset{x}{\min }f(x)$$

根据Fermat定理，直接找到使得${\nabla }_{x}f(x)=0$的点即可。若无解析解，可以使用梯度下降或牛顿方法等使$x$沿负梯度方向逐步逼近极小值点。2

等式约束优化

目标函数加上等式约束条件：
$$\begin{array}{rl}& \underset{x}{\min }f(x)\\ & s.t.h_i(x)=0,i=1,2,...,m\end{array}$$
由于加上了等式约束条件，此时不一定能找到令${\nabla }_{x}f(x)=0$的可行解，只需要在可行域内找到使得$f(x)$取最小值的点。常用的方法为拉格朗日乘子法，利用拉格朗日函数$L(x,\alpha )$：
$$L(x,\alpha )=f(x)+\sum _{i=1}^m{\alpha }_i{h}_i(x)$$
其中${\alpha }_i$为拉格朗日乘子。然后分别对$x$和$\alpha =({\alpha }_1,...,{\alpha }_m{)}^T$求导并令导数为0：

$$\{\begin{array}{rl}{\nabla }_{x}L(x,\alpha )& =0\\ {\nabla }_{\alpha }L(x,\alpha )& =0\end{array}$$
通过求解上述式子，获得极值点。

为什么拉格朗日乘子法能够得到最优值？

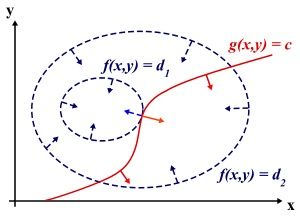
如图所示，满足条件的极值点应该是在目标函数的等高线与约束函数曲线相切的点，即等高线与约束曲线在该点的法向量必须共线，因此最优值必须满足：
$${\nabla }_{x}f(x)=a\times {\nabla }_{x}g(x)$$
这就是上述的${\nabla }_{x}L(x,\alpha )=0$。再加上约束条件$h_i(x)=0$，即${\nabla }_{\alpha }L(x,\alpha )=0$。求解二式，可得到最优解。

不等式约束优化

给定不等式约束问题：
$$\begin{array}{rl}& \underset{x}{\min }f(x)\\ & s.t.h_i(x)=0,i=1,2,...,m\\ & g_j(x)\le 0,j=1,2,...,n\end{array}$$

定义广义拉格朗日函数：
$$L(x,\alpha ,\beta )=f(x)+\sum _{i=1}^m{\alpha }_i{h}_i(x)+\sum _{j=1}^n{\beta }_i{g}_i(x)$$

加上不等式约束后可行解$x$需满足KKT条件：
$$\begin{array}{rl}{\nabla }_{x}L(x,\alpha ,\beta )& =0\\ {\beta }_j{g}_j(x)& =0,j=1,2,...,n\\ h_i(x)& =0,i=1,2,...,m\\ g_j(x)& \le 0,j=1,2,...,n\\ {\beta }_j& \ge 0,j=1,2,...,n\end{array}$$

满足KKT条件后极小化广义拉格朗日函数即可得到在不等式约束条件下的可行解。

对偶问题

关于广义拉格朗日函数有一个重要的结论，即：
$$\underset{\alpha ,\beta ;{\beta }_i\ge 0}{\max }L(x,\alpha ,\beta )=\{\begin{array}{rl}& f(x),x满足原始问题约束\\ & +\infty ,其他\end{array}$$

这很容易证明。当$h_i(x)=0$且$g_j(x)\le 0$时，只需令${\beta }_j=0$，可得$\underset{\alpha ,\beta ;{\beta }_i\ge 0}{\max }L(x,\alpha ,\beta )=f(x)$。这样原始优化问题可转化无约束优化问题：
$$\underset{x}{\min }f(x)=\underset{x}{\min }\underset{\alpha ,\beta ;{\beta }_i\ge 0}{\max }L(x,\alpha ,\beta )$$

定义对偶函数：
$$D(\alpha ,\beta )=\underset{x}{\min }L(x,\alpha ,\beta )$$

则原问题的对偶问题为:
$$\underset{\alpha ,\beta ;{\beta }_i\ge 0}{\max }\underset{x}{\min }L(x,\alpha ,\beta )$$

对偶问题的解$d^{\ast }$与原问题的解$p^{\ast }$满足如下关系：
$$d^{\ast }\le p^{\ast }$$

即对偶问题的解是原问题解的下确界。

在KKT条件下，等式成立，因此我们可以通过求解对偶问题来求解原问题。

参考资料：

1. 广义拉格朗日函数的理解
2. 约束优化方法之拉格朗日乘子法与KKT条件
3. 拉格朗日对偶