Leetcode刷题笔记-array
741. Cherry Pickup
class Solution:
def cherryPickup(self, grid: List[List[int]]) -> int:
# dp[x1][y1][x2] to represent the largest ans we can get when first guy (marked as A) at(x1, y2) and second guy(marked as B) at (x2, x1 + y1 - x2)
# because we can only go right and down, so we have x1 + y1 = x2 + y2 = total steps they go
# https://leetcode.com/problems/cherry-pickup/discuss/165218/Java-O(N3)-DP-solution-w-specific-explanation
# 2. Induction: every time we calculate the maximum of :
# * dp[x1 - 1][y1][x2] : A down, B right
# * dp[x1][y1 - 1][x2] : A right, B right
# * dp[x1 - 1][y1][x2 - 1]: A down, B down
# * dp[x1][y1 - 1][x2 - 1]: A right, B down
# if the Max of these values is negative, then we don't have a path to this point
# else we have: dp[x1][y1][x2] = Max + grid[x1 - 1][y1 - 1] + grid[x2 - 1][y2 - 1](if x1 != x2 && y1 != y2) else we
# only add once.
dp = [[[-1 for _ in grid] for _ in grid] for _ in grid]
dp[0][0][0] = grid[0][0] # base case A and B all in 0 0
n = len(grid)
for x1 in range(0, n):
for y1 in range(0, n):
for x2 in range(0, len(grid)):
y2 = x1 + y1 - x2
if x1 == y1 == x2 == 0 or y2 < 0 or y2 >= n or grid[x1][y1] == -1 or grid[x2][y2] == -1:
continue
pre_max = max(dp[x1-1][y1][x2], dp[x1][y1-1][x2], dp[x1-1][y1][x2-1], dp[x1][y1-1][x2-1])
if pre_max < 0:
continue
dp[x1][y1][x2] = pre_max + grid[x1][y1]
if x1 != x2:
dp[x1][y1][x2] = dp[x1][y1][x2] + grid[x2][y2]
print(x1, y1, x2, y2, dp[x1][y1][x2])
return max(0, dp[-1][-1][-1])723. Candy Crush
class Solution(object):
def candyCrush(self, board):
# 只有横着或者竖着连续3个才可以消去。
# 把满足消去的设置为负数，比如2设置为-2，最后再一起消去
r, c = len(board), len(board[0])
found = True
while found:
found = False
for i in xrange(r):
for j in xrange(c):
val = abs(board[i][j])
if val == 0: continue
# check row
if i + 2 < r and abs(board[i+1][j]) == abs(board[i+2][j]) == val:
found = True
ii = i # 用ii 避免 下面的 i被修改了
while 0 <= ii < r and abs(board[ii][j]) == val: # 这里注意是ii
board[ii][j] = -val
ii += 1
# check col
if j + 2 < c and abs(board[i][j+1]) == abs(board[i][j+2]) == val:
found = True
while 0 <= j < c and abs(board[i][j]) == val:
board[i][j] = -val
j += 1
# 消去
if found:
for j in xrange(c):
emptyRow = r - 1
for i in xrange(r-1, -1, -1):
if board[i][j] > 0:
board[emptyRow][j] = board[i][j]
emptyRow -= 1
for i in xrange(emptyRow, -1, -1):
board[i][j] = 0
return board
562. Longest Line of Consecutive One in Matrix
class Solution(object):
def longestLine(self, M):
maxlen = 0
currlen = collections.defaultdict(int)
for i, row in enumerate(M):
for j, a in enumerate(row):
for key in i, j+.1, i+j+.2, i-j+.3: # j 是列相同的， i+j是anti-diagonals, i-j是diagonals
currlen[key] = (currlen[key] + 1) * a
# currlen[key] += 1*a 是错误的，如果不连续的要断开
maxlen = max(maxlen, currlen[key])
return maxlen
755. Pour Water
class Solution(object):
def pourWater(self, heights, V, K):
for _ in xrange(V):
idx = -1
# check left
for i in xrange(K-1, -1, -1):
if heights[i] > heights[i+1]:
break
elif heights[i] < heights[i+1]:
idx = i
if idx != -1:
heights[idx] += 1
continue
# check right
for i in xrange(K+1, len(heights)):
if heights[i] > heights[i-1]:
break
elif heights[i] < heights[i-1]:
idx = i
if idx != -1:
heights[idx] += 1
else:
heights[K] += 1
return heights
https://leetcode.com/problems/pour-water/description/
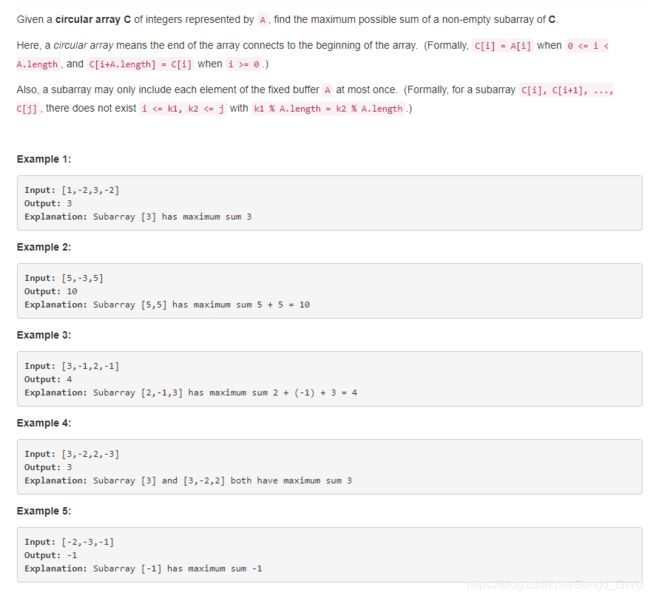
918. Maximum Sum Circular Subarray
class Solution(object):
def maxSubarraySumCircular(self, A):
total = curMax = curMin = 0
maxSum = float('-inf')
minSum = float('inf')
for n in A:
total += n
curMax = max(n, curMax+n)
maxSum = max(maxSum, curMax)
curMin = min(n, curMin+n)
minSum = min(minSum, curMin)
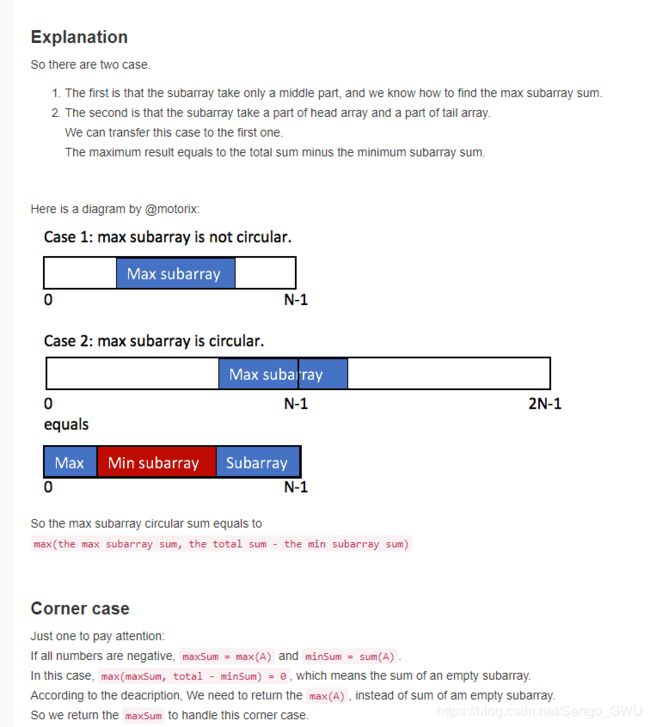
return max(maxSum, total - minSum) if maxSum > 0 else maxSum
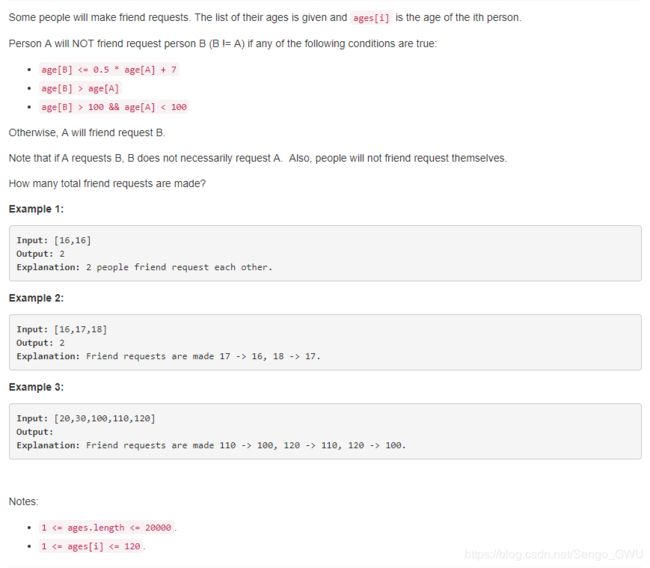
825. Friends Of Appropriate Ages
class Solution(object):
def numFriendRequests(self, ages):
A = [0] * 121
re = 0
for age in ages:
A[age] += 1
# A < B <= 0.5A + 7, A < 0.5A + 7 A < 15 can not make friend request
for a in xrange(15, 121):
for b in xrange(int(0.5*a)+7+1, a+1):
re += A[a] * A[b] if a != b else A[a] * (A[b]-1)
return re243. Shortest Word Distance
class Solution(object):
def shortestDistance(self, words, word1, word2):
i1 = i2 = -1
re = 5000
for idx, w in enumerate(words):
if w == word1:
i1 = idx
if w == word2:
i2 = idx
if i1 != -1 and i2 != -1:
re = min(re, abs(i1-i2))
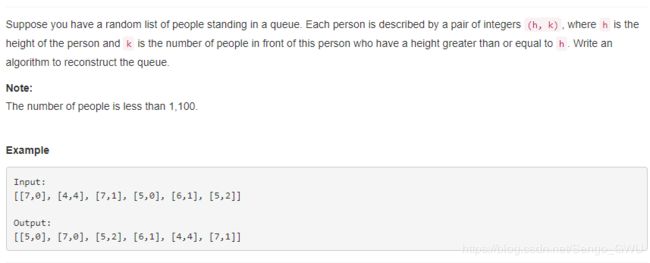
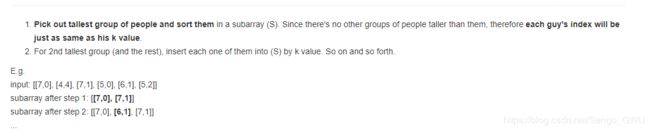
return re406. Queue Reconstruction by Height
class Solution(object):
def reconstructQueue(self, people):
d = {}
for h, k in people:
if h not in d:
d[h] = [[h, k]]
else:
d[h].append([h, k])
re = []
for h in sorted(d.keys(), reverse=True):
group = sorted(d[h])
if not re:
re += group
else:
for h, k in group:
re.insert(k, [h, k])
return re
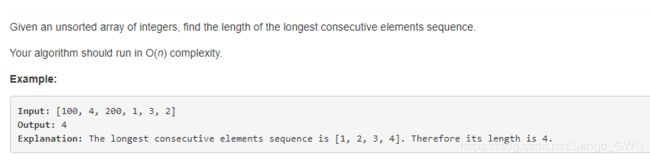
128. Longest Consecutive Sequence
class Solution(object):
def longestConsecutive(self, nums):
d = {}
res = 0
for n in nums:
if n in d:
continue
left = d.get(n-1, 0)
right = d.get(n+1, 0)
Sum = left + right + 1
res = max(res, Sum)
d[n] = Sum
d[n-left] = Sum # 边缘的2个更新Sum就可以了，中间连续的不需要
d[n+right] = Sum
return res
718. Maximum Length of Repeated Subarray
DP解法
Given two integer arrays A and B, return the maximum length of an subarray that appears in both arrays.
Example 1:
Input:
A: [1,2,3,2,1]
B: [3,2,1,4,7]
Output: 3
Explanation:
The repeated subarray with maximum length is [3, 2, 1].dp[i][j] 的i,j是指的A，B的长度，而不是A，B的下标。比如dp[1][0]是指的长度为1的A 和长度为0的B的位置的比较。当i或者j为0时候，因为长度为0所以重复0，则dp为0. 遍历所有子串，记录重复的长度。
class Solution(object):
def findLength(self, A, B):
"""
:type A: List[int]
:type B: List[int]
:rtype: int
"""
dp = [[0]*(len(B)+1) for i in xrange(len(A)+1)]
maxLen = 0
for i in xrange(1, len(A)+1):
for j in xrange(1, len(B)+1):
if A[i-1] == B[j-1]:
dp[i][j] = dp[i-1][j-1]+1
maxLen = max(maxLen, dp[i][j])
else:
dp[i][j] = 0
return maxLen
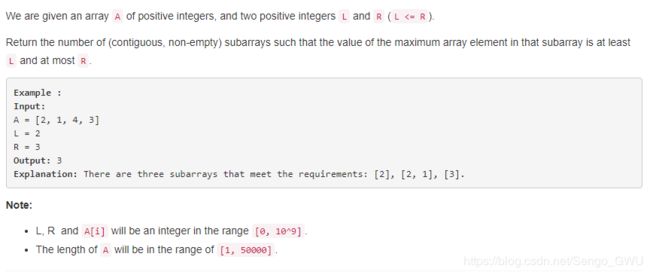
795. Number of Subarrays with Bounded Maximum
DP
Suppose dp[i] denotes the max number of valid sub-array ending with A[i]. We use following example to illustrate the idea:
A = [2, 1, 4, 2, 3], L = 2, R = 3
- if A[i] < L
For example, i = 1. We can only append A[i] to a valid sub-array ending with A[i-1] to create new sub-array. So we have dp[i] = dp[i-1] (for i > 0)
- if A[i] > R:
For example, i = 2. No valid sub-array ending with A[i] exist. So we have dp[i] = 0.
We also record the position of the invalid number 4 here as prev.
- if L <= A[i] <= R
For example, i = 4. In this case any sub-array starts after the previous invalid number to A[i] (A[prev+1..i], A[prev+2..i]) is a new valid sub-array. So dp[i] += i - prev
Finally the sum of the dp array is the solution. Meanwhile, notice dp[i] only relies on dp[i-1] (and also prev), we can reduce the space complexity to O(1)
class Solution(object):
def numSubarrayBoundedMax(self, A, L, R):
"""
:type A: List[int]
:type L: int
:type R: int
:rtype: int
"""
dp = 0
prev = -1
res = 0
for i in xrange(len(A)):
if L<= A[i] <= R:
dp = i - prev
res += dp
elif A[i] < L:
res += dp
else:
dp = 0
prev = i
return res分治法，第K小的数 O（n）
873. Length of Longest Fibonacci Subsequence
A sequence X_1, X_2, ..., X_n is fibonacci-like if:
n >= 3X_i + X_{i+1} = X_{i+2}for alli + 2 <= n
Given a strictly increasing array A of positive integers forming a sequence, find the length of the longest fibonacci-like subsequence of A. If one does not exist, return 0.
(Recall that a subsequence is derived from another sequence A by deleting any number of elements (including none) from A, without changing the order of the remaining elements. For example, [3, 5, 8] is a subsequence of [3, 4, 5, 6, 7, 8].)
Example 1:
Input: [1,2,3,4,5,6,7,8]
Output: 5
Explanation:
The longest subsequence that is fibonacci-like: [1,2,3,5,8].
Example 2:
Input: [1,3,7,11,12,14,18]
Output: 3
Explanation:
The longest subsequence that is fibonacci-like:
[1,11,12], [3,11,14] or [7,11,18].dp[i][j] 表示以A[i] 和A[j]结尾的Fib序列的长度。则dp[i][j] = 以 A[j] 和 A[i]-A[j] 结尾的序列。所以要判断A[i]-A[j]是否在A中，并且，A【i】-A[j]要小于A【j】
第一次尝试，通过了23次时，时间超过限制：
class Solution(object):
def lenLongestFibSubseq(self, A):
"""
:type A: List[int]
:rtype: int
"""
dp = [[2]*i for i in A]
maxLen = 0
for i in xrange(len(A)):
for j in xrange(i):
if A[i] - A[j] < A[j] and (A[i]-A[j]) in A:
dp[i][j] = dp[j][A.index(A[i]-A[j])] + 1
maxLen = max(maxLen, dp[i][j])
return maxLen改进后：
class Solution(object):
def lenLongestFibSubseq(self, A):
"""
:type A: List[int]
:rtype: int
"""
dp = collections.defaultdict(int)
maxLen = 0
s = set(A)
for i in xrange(len(A)):
for j in xrange(i):
if A[i] - A[j] < A[j] and (A[i]-A[j]) in s:
dp[A[i], A[j]] = dp.get((A[j], A[i]-A[j]), 2) + 1
maxLen = max(maxLen, dp[A[i], A[j]])
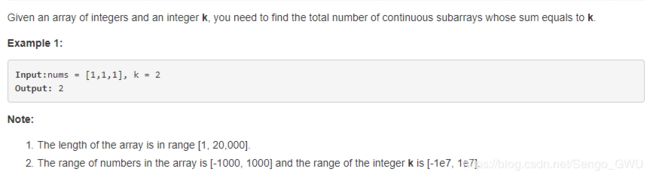
return maxLen560. Subarray Sum Equals K
第一个解法，时间超过限制，但是简单易懂：class Solution(object):
def subarraySum(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: int
"""
res = []
for i in xrange(len(nums)):
self.helper(nums[i+1:], k-nums[i], res)
return len(res)
def helper(self, nums, k, res):
if k == 0:
res.append(1)
if not nums:
return
self.helper(nums[1:], k-nums[0], res)第二次解法，这个解法也是网上最推崇的。
1.记录 nums[0]+nums[1] + ... nums[j] = _sum 的次数，
2.然后找到期中从0开始加到j 等于_sum - k的个数
3.res += 上面的个数
解释：比如说 A+B+C+D+E = SUM, 我们要找和为K的连续子序列。其中，A+B+C的和为SUM-K, 那么D+E的和就肯定为K。
或者说如果C+D+E=K 那么A+B 就一定是SUM-K。如果存在从index=0开始的子序列和为SUM-K（ABC），那么在SUM的子序列里面必然存在和为K的子序列(DE)。 所以我们不直接找和为K的子序列，而是直接找从index=0开始sum为SUM-K的子序列的个数。
count[0] = 1 是关键。
class Solution(object):
def subarraySum(self, nums, k):
re = Sum = 0
d = {}
d[0] = 1
for n in nums:
Sum += n
re += d.get(Sum-k, 0)
d[Sum] = d.get(Sum, 0) + 1
return re
75. Sort Colors
- A rather straight forward solution is a two-pass algorithm using counting sort.
First, iterate the array counting number of 0's, 1's, and 2's, then overwrite array with total number of 0's, then 1's and followed by 2's.
Two-pass解法太暴力了，下面介绍一种通用的排序算法。参考自视频：
https://www.youtube.com/watch?v=jsHJtfZRwUw
class Solution(object):
def sortColors(self, nums):
"""
:type nums: List[int]
:rtype: void Do not return anything, modify nums in-place instead.
"""
left = index = 0
right = len(nums)-1
while index<=right:
if nums[index] == 0:
nums[left], nums[index] = 0, nums[left]
index += 1
left += 1
elif nums[index] == 1:
index += 1
elif nums[index] == 2:
nums[right], nums[index] = 2, nums[right]
right -= 1
定义一个left,right 指针和Index指针，当nums[index]=2的时候 index是不加1的，为了防止如0和2交换时候，还要继续把0和left交换。
870. Advantage Shuffle
Given two arrays A and B of equal size, the advantage of A with respect to B is the number of indices i for which A[i] > B[i].
Return any permutation of A that maximizes its advantage with respect to B.
Example 1:
Input: A = [2,7,11,15], B = [1,10,4,11]
Output: [2,11,7,15]
Example 2:
Input: A = [12,24,8,32], B = [13,25,32,11]
Output: [24,32,8,12]第一次解法，超过时间限制，59 / 67 test cases passed.
把A和B 都排序，从后往前比较，如果B【i】>=A【i】,那么B【i】对应的值就取A剩下的最小值，否则取A的最大值，然后在A里面把该值弹出。就像是田忌赛马一样，把A最差的马给B最厉害的马。
class Solution(object):
def advantageCount(self, A, B):
"""
:type A: List[int]
:type B: List[int]
:rtype: List[int]
"""
A = sorted(A)
b = sorted(B)
re = []
for i in xrange(len(b)):
index = len(b) - i - 1
if b[index] >= A[-1]:
re.append(A.pop(0))
else:
re.append(A.pop(-1))
re = re[::-1]
res = []
for i in xrange(len(b)):
res.append(re[b.index(B[i])])
b[b.index(B[i])] = None
return res改进后：把B每个值的索引放到B里面，然后再排序B：
class Solution(object):
def advantageCount(self, A, B):
"""
:type A: List[int]
:type B: List[int]
:rtype: List[int]
"""
A = sorted(A)
length = len(B)
re = [n for n in A]
for i in xrange(length):
B[i] = (B[i], i)
B = sorted(B)
for i in xrange(length):
index = length - i - 1
if B[index][0] >= A[-1]:
re[B[index][1]] = A.pop(0)
else:
re[B[index][1]] = A.pop(-1)
return re670. Maximum Swap
Given a non-negative integer, you could swap two digits at most once to get the maximum valued number. Return the maximum valued number you could get.
Example 1:
Input: 2736
Output: 7236
Explanation: Swap the number 2 and the number 7.
Example 2:
Input: 9973
Output: 9973
Explanation: No swap.
class Solution(object):
def maximumSwap(self, num):
"""
:type num: int
:rtype: int
"""
numList = [int(x) for x in str(num)]
# 记录0-9 最后出现的位置
bucket = [0] * 10
for i in xrange(len(numList)):
bucket[numList[i]] = i
for i in xrange(len(numList)):
for j in xrange(9, numList[i], -1):
if bucket[j] > i:
numList[i], numList[bucket[j]] = numList[bucket[j]], numList[i]
return int("".join(str(n) for n in numList))
return num792. Number of Matching Subsequences
Given string S and a dictionary of words words, find the number of words[i] that is a subsequence of S.
Example : Input: S = "abcde" words = ["a", "bb", "acd", "ace"] Output: 3 Explanation: There are three words inwordsthat are a subsequence ofS: "a", "acd", "ace".
第一次尝试，超过时间限制，27 / 49 test cases passed.：
class Solution(object):
def numMatchingSubseq(self, S, words):
"""
:type S: str
:type words: List[str]
:rtype: int
"""
res = 0
for word in words:
cur = S[:]
i = 0
for letter in word:
if letter in cur:
index = cur.index(letter)
cur = cur[index+1:]
if i == len(word)-1:
res += 1
else:
break
i += 1
return res参考这篇文章的方法改进后：https://leetcode.com/problems/number-of-matching-subsequences/discuss/117578/Simple-Python-solution
class Solution(object):
def numMatchingSubseq(self, S, words):
"""
:type S: str
:type words: List[str]
:rtype: int
"""
def find_index(letter, index_s, pointer):
ids = index_s.get(letter)
if not ids:
return False
for i in ids:
if i >= pointer:
return i+1
return False
index_s = {key: [] for key in S}
res = 0
for index, key in enumerate(list(S)):
index_s[key].append(index)
for w in words: # w is each word
p = 0
for i in xrange(len(w)): # l is each letter in a word
p = find_index(w[i], index_s, p)
if not p:
break
if i == len(w)-1:
res += 1
return res11. Container With Most Water
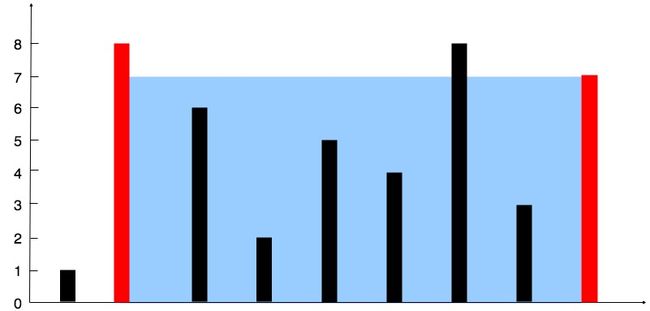
Given n non-negative integers a1, a2, ..., an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.
Note: You may not slant the container and n is at least 2.
The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.
Example:
Input: [1,8,6,2,5,4,8,3,7]
Output: 49def maxArea(self, height):
"""
:type height: List[int]
:rtype: int
"""
i = 0 # i points to the beginning
j = len(height) - 1 # j points to the end
max_area = 0
while i < j: # i and j will get closer to eachother but never pass, ensuring every element is only visited once
width = abs(i-j) # the distance between i and j, set before i or j is reassigned
if height[i] < height[j]: # the lower wall dictates vertical distance bc gravity
h = height[i]
i += 1 # if the i wall is lower, move forward to try to find a taller wall
else:
h = height[j]
j -= 1 # if the j wall is lower, move backwards to try to find a taller wall
max_area = max(max_area, h * width)
return max_area42. Trapping Rain Water
class Solution(object):
def trap(self, height):
"""
:type height: List[int]
:rtype: int
"""
if not height or len(height) < 3:
return 0
left, right = 0, len(height) - 1
leftMax, rightMax = height[left], height[right]
volumn = 0
while left < right:
leftMax = max(leftMax, height[left])
rightMax = max(rightMax, height[right])
if leftMax <= rightMax:
volumn += leftMax - height[left]
left += 1
else:
volumn += rightMax - height[right]
right -= 1
return volumn73. Set Matrix Zeroes
Given a m x n matrix, if an element is 0, set its entire row and column to 0. Do it in-place.
Example 1:
Input:
[
[1,1,1],
[1,0,1],
[1,1,1]
]
Output:
[
[1,0,1],
[0,0,0],
[1,0,1]
]
Example 2:
Input:
[
[0,1,2,0],
[3,4,5,2],
[1,3,1,5]
]
Output:
[
[0,0,0,0],
[0,4,5,0],
[0,3,1,0]
]
Follow up:
- A straight forward solution using O(mn) space is probably a bad idea.
- A simple improvement uses O(m + n) space, but still not the best solution.
- Could you devise a constant space solution?
class Solution(object):
def setZeroes(self, matrix):
"""
:type matrix: List[List[int]]
:rtype: void Do not return anything, modify matrix in-place instead.
"""
row, col = len(matrix), len(matrix[0])
badRow, badCol = set(), set()
for i in xrange(row):
for j in xrange(col):
if not matrix[i][j]:
badRow.add(i)
badCol.add(j)
for r in badRow:
matrix[r] = [0] * col
for c in badCol:
for r in xrange(row):
matrix[r][c] = 0120. Triangle
DP
Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.
For example, given the following triangle
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).
Note:
Bonus point if you are able to do this using only O(n) extra space, where n is the total number of rows in the triangle.
class Solution(object):
def minimumTotal(self, triangle):
"""
:type triangle: List[List[int]]
:rtype: int
"""
# DP[i][j] = triangle[i][j] + mind(DP[i-1][j], DP[i-1][j-1])
for i in xrange(1, len(triangle)):
for j in xrange(0, i+1):
if j == 0:
triangle[i][j] = triangle[i][j] + triangle[i-1][j]
elif j == i:
triangle[i][j] = triangle[i][j] + triangle[i-1][j-1]
else:
triangle[i][j] = triangle[i][j] + min(triangle[i-1][j], triangle[i-1][j-1])
return min(triangle[len(triangle)-1])bottom up
class Solution(object):
def minimumTotal(self, triangle):
f = [0] * (len(triangle) + 1)
for row in triangle[::-1]:
for i in xrange(len(row)):
f[i] = row[i] + min(f[i], f[i + 1])
return f[0]
209. Minimum Size Subarray Sum
Given an array of n positive integers and a positive integer s, find the minimal length of a contiguous subarray of which the sum ≥ s. If there isn't one, return 0 instead.
Example:
Input:s = 7, nums = [2,3,1,2,4,3]Output: 2 Explanation: the subarray[4,3]has the minimal length under the problem constraint.
第一次尝试，过段超时。14 / 15 test cases passed. 这是O（n^2）的解法。
class Solution(object):
def minSubArrayLen(self, k, nums):
"""
:type s: int
:type nums: List[int]
:rtype: int
"""
s = 0
res = float('inf')
for i in xrange(len(nums)):
s += nums[i]
if s>=k:
_s = 0
count = 0
while _s < k:
count += 1
_s += nums[i]
i -= 1
res = min(res, count)
return res if res != float('inf') else 0参考了答案改成O（2n）的解法：
class Solution(object):
def minSubArrayLen(self, k, nums):
"""
:type s: int
:type nums: List[int]
:rtype: int
"""
s = 0
res = float('inf')
left = 0
for i in xrange(len(nums)):
s += nums[i]
while s >= k:
s -= nums[left]
res = min(res, i-left+1)
left += 1
return res if res != float('inf') else 0
56. Merge Intervals
Given a collection of intervals, merge all overlapping intervals.
Example 1:
Input: [[1,3],[2,6],[8,10],[15,18]]
Output: [[1,6],[8,10],[15,18]]
Explanation: Since intervals [1,3] and [2,6] overlaps, merge them into [1,6].
Example 2:
Input: [[1,4],[4,5]]
Output: [[1,5]]
Explanation: Intervals [1,4] and [4,5] are considerred overlapping.# Definition for an interval.
# class Interval(object):
# def __init__(self, s=0, e=0):
# self.start = s
# self.end = e
class Solution(object):
def merge(self, intervals):
"""
:type intervals: List[Interval]
:rtype: List[Interval]
"""
if len(intervals) == 0: return []
intervals = sorted(intervals, key = lambda x: x.start)
res = [intervals[0]]
for inter in intervals[1:]:
if res[-1].end >= inter.start:
res[-1].end = max(inter.end, res[-1].end)
else:
res.append(inter)
return res57. Insert Interval
# Definition for an interval.
# class Interval(object):
# def __init__(self, s=0, e=0):
# self.start = s
# self.end = e
class Solution(object):
def insert(self, intervals, newInterval):
"""
:type intervals: List[Interval]
:type newInterval: Interval
:rtype: List[Interval]
"""
# 把newInter 按start的大小插入 intervals里面
insert = [newInterval]
for idx, inter in enumerate(intervals):
if inter.start > newInterval.start:
intervals.insert(idx, insert.pop())
break
intervals += insert
# 插入后 剩下的 56. Merge Intervals 一样了
res = [intervals[0]]
for inter in intervals[1:]:
if res[-1].end >= inter.start:
res[-1].end = max(res[-1].end, inter.end)
else:
res.append(inter)
return res
55. Jump Game
Given an array of non-negative integers, you are initially positioned at the first index of the array.
Each element in the array represents your maximum jump length at that position.
Determine if you are able to reach the last index.
Example 1:
Input: [2,3,1,1,4]
Output: true
Explanation: Jump 1 step from index 0 to 1, then 3 steps to the last index.
Example 2:
Input: [3,2,1,0,4]
Output: false
Explanation: You will always arrive at index 3 no matter what. Its maximum
jump length is 0, which makes it impossible to reach the last index.贪心算法。记录当前位置最远可以到达的位置 max_reach。 可以到达的位置为当前索引位置加可以最远走的距离即：i+nums[i],和前面的max_reach取最大值。
class Solution(object):
def canJump(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""
max_reach = 0
for i in xrange(len(nums)):
if i > max_reach:
return False
max_reach = max(max_reach, i+nums[i])
return True229. Majority Element II
Majority Voting Algorithm, 多数投票算法 https://gregable.com/2013/10/majority-vote-algorithm-find-majority.html
Given an integer array of size n, find all elements that appear more than ⌊ n/3 ⌋ times.
Note: The algorithm should run in linear time and in O(1) space.
Example 1:
Input: [3,2,3]
Output: [3]Example 2:
Input: [1,1,1,3,3,2,2,2]
Output: [1,2]class Solution(object):
def majorityElement(self, nums):
"""
:type nums: List[int]
:rtype: List[int]
"""
length = len(nums) / 3
num1, num2, c1, c2 = 0, 1, 0, 0
for n in nums:
if n == num1:
c1 += 1
elif n == num2:
c2 += 1
elif c1 == 0:
num1 = n
c1 = 1
elif c2 == 0:
num2 = n
c2 = 1
else:
c1 -= 1
c2 -= 1
return [n for n in (num1, num2) if nums.count(n) > length]31. Next Permutation
参考视频https://www.youtube.com/watch?v=9mdoM2dVid8
Implement next permutation, which rearranges numbers into the lexicographically next greater permutation of numbers.
If such arrangement is not possible, it must rearrange it as the lowest possible order (ie, sorted in ascending order).
The replacement must be in-place and use only constant extra memory.
Here are some examples. Inputs are in the left-hand column and its corresponding outputs are in the right-hand column.
1,2,3 → 1,3,23,2,1 → 1,2,31,1,5 → 1,5,1
class Solution(object):
def nextPermutation(self, nums):
"""
:type nums: List[int]
:rtype: void Do not return anything, modify nums in-place instead.
"""
# 1 2 7 4 3 1
# 1 [2] 7 4 3 1
# 1 2 7 4 [3] 1
# 1 [3] 7 4 [2] 1
# 1 3 1 2 4 7 reverse 7421
length = len(nums)
# find 2
firstSmall = -1
for i in xrange(length-2, -1, -1):
if nums[i] < nums[i+1]:
firstSmall = i
break
if firstSmall == -1: # 321 reverse
left, right = 0, length-1
while left < right:
nums[left], nums[right] = nums[right], nums[left]
left += 1
right -= 1
return
# find 3
firstLarge = 0
i = length - 1
while i >= 0:
if nums[i] > nums[firstSmall]:
firstLarge = i
break
i -= 1
# swap 2 and 3
nums[firstSmall], nums[firstLarge] = nums[firstLarge], nums[firstSmall]
# reverse
left = firstSmall + 1
right = length - 1
while left < right:
nums[left], nums[right] = nums[right], nums[left]
left += 1
right -= 1
return
15. 3Sum
Given an array nums of n integers, are there elements a, b, c in nums such that a + b + c = 0? Find all unique triplets in the array which gives the sum of zero.
Note:
The solution set must not contain duplicate triplets.
Example:
Given array nums = [-1, 0, 1, 2, -1, -4],
A solution set is:
[
[-1, 0, 1],
[-1, -1, 2]
]2SUM 3SUM 4SUM 要一起总结
3sum参考视频https://www.youtube.com/watch?v=gq-uWp327m8
class Solution(object):
def threeSum(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
length = len(nums)
nums = sorted(nums)
res = []
for i in xrange(length - 2):
if i > 0 and nums[i] == nums[i-1]:
continue
left, right = i+1, length-1
while left 0 and nums[right] == nums[right+1]:
right -= 1
elif s > 0:
right -= 1
while right-1 > 0 and nums[right] == nums[right+1]:
right -= 1
else:
left += 1
while left+1 < length-1 and nums[left] == nums[left-1]:
left += 1
return res 923. 3Sum With Multiplicity
class Solution(object):
def threeSumMulti(self, A, target):
MOD = 10**9 + 7
res = 0
count = collections.Counter(A)
keys = sorted(count)
# x, y, z are keys
for i, x in enumerate(keys):
j, k = i, len(keys)-1
while j <= k:
y, z = keys[j], keys[k]
if x + y + z < target:
j += 1
elif x + y + z > target:
k -= 1
else:
if i < j < k:
res += count[x] * count[y] * count[z]
elif i < j == k:
res += count[x] * count[y] * (count[y]-1) / 2 # C[n, 2] n里个里面选2个
elif i == j < k:
res += count[x] * (count[x] - 1) / 2 * count[z]
elif i == j == k:
res += count[x] * (count[x]-1) * (count[x]-2) / 3 / 2 # C[n, 3]
j += 1 # 注意
k -= 1
return res % MOD
16. 3Sum Closest
class Solution(object):
def threeSumClosest(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: int
"""
re = sys.maxint
nums = sorted(nums)
for i in xrange(len(nums)-2):
if i > 0 and nums[i] == nums[i-1]:
continue
j, k = i+1, len(nums)-1
while j < k:
s = nums[i] + nums[j] + nums[k]
if s == target:
return s
if abs(s - target) < abs(target - re):
re = s
if s < target:
j += 1
else:
k -= 1
return re
18. 4Sum
Given an array nums of n integers and an integer target, are there elements a, b, c, and d in nums such that a + b + c + d = target? Find all unique quadruplets in the array which gives the sum of target.
Note:
The solution set must not contain duplicate quadruplets.
Example:
Given array nums = [1, 0, -1, 0, -2, 2], and target = 0.
A solution set is:
[
[-1, 0, 0, 1],
[-2, -1, 1, 2],
[-2, 0, 0, 2]
]第一次尝试，回溯法，超过时间。
| 217 / 282 test cases passed. |
class Solution(object):
def fourSum(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[List[int]]
"""
res = []
self.helper(nums, target, [], res)
return res
def helper(self, nums, target, cur, res):
if len(cur) == 4 and target == 0:
cur = sorted(cur)
if cur not in res:
res.append(cur)
return
if len(cur) > 4:
return
for i in xrange(len(nums)):
self.helper(nums[i+1:], target-nums[i], cur+[nums[i]], res)
直接3SUM 改编的。记得要先排序下Nums
class Solution(object):
def fourSum(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[List[int]]
"""
length = len(nums)
res = []
nums = sorted(nums)
for i in xrange(length-3):
if i > 0 and nums[i] == nums[i-1]:
continue
for j in xrange(i+1, length-2):
if j > i+1 and nums[j] == nums[j-1]:
continue
left, right = j+1, length-1
while left < right:
s = nums[i] + nums[j] + nums[left] + nums[right]
if s == target:
res.append([nums[i], nums[j], nums[left], nums[right]])
left += 1
right -= 1
while left+1 < length-1 and nums[left] == nums[left-1]:
left += 1
while right-1 > 0 and nums[right] == nums[right+1]:
right -= 1
elif s > target:
right -= 1
while right-1 > 0 and nums[right] == nums[right+1]:
right -= 1
else:
left += 1
while left+1 < length-1 and nums[left] == nums[left-1]:
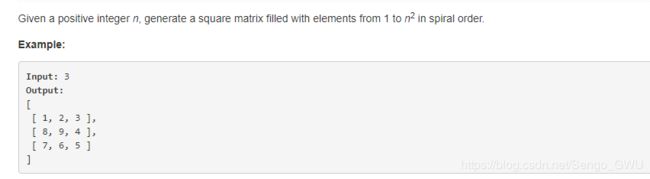
return res54. Spiral Matrix
Given a matrix of m x n elements (m rows, n columns), return all elements of the matrix in spiral order.
Example 1:
Input:
[
[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]
]
Output: [1,2,3,6,9,8,7,4,5]
Example 2:
Input:
[
[1, 2, 3, 4],
[5, 6, 7, 8],
[9,10,11,12]
]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]class Solution(object):
def spiralOrder(self, matrix):
"""
:type matrix: List[List[int]]
:rtype: List[int]
"""
if not matrix:
return []
rowBegin = 0
rowEnd = len(matrix)
colBegin = 0
colEnd = len(matrix[0])
res = []
while rowBegin59. Spiral Matrix II
应该用for i in xrange的 这样就不需要 while-- else
class Solution(object):
def generateMatrix(self, n):
"""
:type n: int
:rtype: List[List[int]]
"""
M = [[0] * n for _ in xrange(n)]
minRow = minCol = row = col = 0
upRow = upCol = n-1
value = 1
while minRow <= row <= upRow and minCol <= col <= upCol:
while col <= upCol:
# print row, col, value
M[row][col] = value
value += 1
col += 1
else:
col -= 1
minRow += 1
row += 1
while row <= upRow:
# print row, col, value
M[row][col] = value
value += 1
row += 1
else:
row -= 1
upCol -= 1
col -= 1
while col >= minCol:
# print row, col, value
M[row][col] = value
value += 1
col -= 1
else:
col += 1
upRow -= 1
row -= 1
while row >= minRow:
# print row, col, value
M[row][col] = value
value += 1
row -= 1
else:
row += 1
minCol += 1
col += 1
return M
70. Climbing Stairs DP easy
You are climbing a stair case. It takes n steps to reach to the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
Note: Given n will be a positive integer.
Example 1:
Input: 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
Example 2:
Input: 3
Output: 3
Explanation: There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
class Solution(object):
def climbStairs(self, n):
"""
:type n: int
:rtype: int
"""
dp = [0 for i in xrange(n+1)]
dp[0] = dp[1] = 1
for i in xrange(2, n+1):
dp[i] = dp[i-2] + dp[i-1]
return dp[-1]338. Counting Bits
dp
Given a non negative integer number num. For every numbers i in the range 0 ≤ i ≤ num calculate the number of 1's in their binary representation and return them as an array.
Example 1:
Input: 2
Output: [0,1,1]Example 2:
Input: 5
Output: [0,1,1,2,1,2]
class Solution(object):
def countBits(self, num):
"""
:type num: int
:rtype: List[int]
"""
dp = [0 for x in xrange(num+1)]
for i in xrange(num+1):
dp[i] = dp[i//2] + i%2
return [i for i in dp]413. Arithmetic Slices dp
A sequence of number is called arithmetic if it consists of at least three elements and if the difference between any two consecutive elements is the same.
For example, these are arithmetic sequence:
1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9The following sequence is not arithmetic.
1, 1, 2, 5, 7
A zero-indexed array A consisting of N numbers is given. A slice of that array is any pair of integers (P, Q) such that 0 <= P < Q < N.
A slice (P, Q) of array A is called arithmetic if the sequence:
A[P], A[p + 1], ..., A[Q - 1], A[Q] is arithmetic. In particular, this means that P + 1 < Q.
The function should return the number of arithmetic slices in the array A.
Example:
A = [1, 2, 3, 4]
return: 3, for 3 arithmetic slices in A: [1, 2, 3], [2, 3, 4] and [1, 2, 3, 4] itself.class Solution(object):
def numberOfArithmeticSlices(self, A):
"""
:type A: List[int]
:rtype: int
"""
total = 0
cur = 0
for i in xrange(2, len(A)):
if A[i]-A[i-1] == A[i-1]-A[i-2]:
cur += 1
total += cur
else:
cur = 0
return total
712. Minimum ASCII Delete Sum for Two Strings
Given two strings s1, s2, find the lowest ASCII sum of deleted characters to make two strings equal.
Example 1:
Input: s1 = "sea", s2 = "eat"
Output: 231
Explanation: Deleting "s" from "sea" adds the ASCII value of "s" (115) to the sum.
Deleting "t" from "eat" adds 116 to the sum.
At the end, both strings are equal, and 115 + 116 = 231 is the minimum sum possible to achieve this.
Example 2:
Input: s1 = "delete", s2 = "leet"
Output: 403
Explanation: Deleting "dee" from "delete" to turn the string into "let",
adds 100[d]+101[e]+101[e] to the sum. Deleting "e" from "leet" adds 101[e] to the sum.
At the end, both strings are equal to "let", and the answer is 100+101+101+101 = 403.
If instead we turned both strings into "lee" or "eet", we would get answers of 433 or 417, which are higher.to get the minimal cost, we need to find the common subsequences, and among all the common subsequences, we need to find the minimal cost.
it is very like to find the longest common subsequence, but this time, we need to find the max ascii common subsequence, then the minimal cost is the two fixed ascii sum of two origin strings, minus the max ascii common subsequence we have found.
class Solution(object):
def minimumDeleteSum(self, s1, s2):
"""
:type s1: str
:type s2: str
:rtype: int
"""
l1 = len(s1)
l2 = len(s2)
dp = [[0]*(l2+1) for i in xrange(l1+1)]
for i in xrange(l1):
for j in xrange(l2):
if s1[i] == s2[j]:
dp[i+1][j+1] = dp[i][j] + 2*ord(s1[i])
else:
dp[i+1][j+1] = max(dp[i][j+1], dp[i+1][j])
n1 = sum(ord(c) for c in s1)
n2 = sum(ord(c) for c in s2)
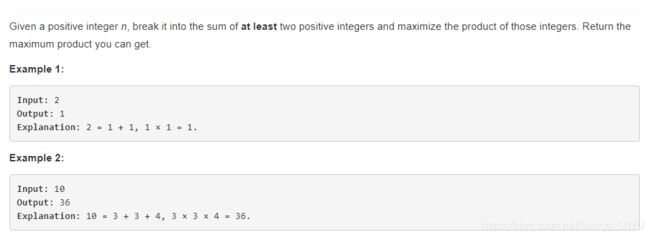
return n1 + n2 - dp[-1][-1]343. Integer Break 尽量多的乘以3，总的乘积最大
The first thing we should consider is : What is the max product if we break a number N into two factors?
I use a function to express this product: f=x(N-x)
When x=N/2, we get the maximum of this function.
However, factors should be integers. Thus the maximum is (N/2)*(N/2) when N is even or (N-1)/2 *(N+1)/2 when N is odd.
When the maximum of f is larger than N, we should do the break.
(N/2)*(N/2)>=N, then N>=4
(N-1)/2 *(N+1)/2>=N, then N>=5
These two expressions mean that factors should be less than 4, otherwise we can do the break and get a better product. The factors in last result should be 1, 2 or 3. Obviously, 1 should be abandoned. Thus, the factors of the perfect product should be 2 or 3.
The reason why we should use 3 as many as possible is
For 6, 3 * 3>2 * 2 * 2. Thus, the optimal product should contain no more than three 2.
Below is my accepted, O(N) solution.
public class Solution {
public int integerBreak(int n) {
if(n==2) return 1;
if(n==3) return 2;
int product = 1;
while(n>4){
product*=3;
n-=3;
}
product*=n;
return product;
}
}650. 2 Keys Keyboard
class Solution(object):
def minSteps(self, n):
"""
:type n: int
:rtype: int
"""
dp = [0, 0]
for i in xrange(2, n+1):
dp.append(i)
j = i-1
for j in xrange(j, 0, -1):
if i%j == 0:
dp[i] = dp[j] + i/j
break
return dp[n]As per the keyboard operations:
to get AA from A we need 2 additional steps (copy-all and then paste)
to get AAA from A we need 3 additional steps (copy-all, then paste, then again paste)
For generating AAAA we need 2 additional steps from AA.
however, to get AAAAAAAA, the most optimal way would be from AAAA, with 2 additional steps (copy-all then paste)
Essentially, we find the next smaller length sequence (than the one under consideration) which can be copied and then pasted over multiple times to generate the desired sequence. The moment we find a length that divides our required sequence length perfectly, then we don't need to check for any smaller length sequences.
// if sequence of length 'j' can be pasted multiple times to get length 'i' sequence
if (i % j == 0) {
// we just need to paste sequence j (i/j - 1) times, hence additional (i/j) times since we need to copy it first as well.
// we don't need checking any smaller length sequences
dp[i] = dp[j] + (i/j);
break;
}486. Predict the Winner DP 计划递归
https://www.youtube.com/watch?v=g5wLHFTodm0
Given an array of scores that are non-negative integers. Player 1 picks one of the numbers from either end of the array followed by the player 2 and then player 1 and so on. Each time a player picks a number, that number will not be available for the next player. This continues until all the scores have been chosen. The player with the maximum score wins.
Given an array of scores, predict whether player 1 is the winner. You can assume each player plays to maximize his score.
Example 1:
Input: [1, 5, 2]
Output: False
Explanation: Initially, player 1 can choose between 1 and 2.
If he chooses 2 (or 1), then player 2 can choose from 1 (or 2) and 5. If player 2 chooses 5, then player 1 will be left with 1 (or 2).
So, final score of player 1 is 1 + 2 = 3, and player 2 is 5.
Hence, player 1 will never be the winner and you need to return False.
Example 2:
Input: [1, 5, 233, 7]
Output: True
Explanation: Player 1 first chooses 1. Then player 2 have to choose between 5 and 7. No matter which number player 2 choose, player 1 can choose 233.
Finally, player 1 has more score (234) than player 2 (12), so you need to return True representing player1 can win.
Note:
- 1 <= length of the array <= 20.
- Any scores in the given array are non-negative integers and will not exceed 10,000,000.
- If the scores of both players are equal, then player 1 is still the winner.
递归，超过时间限制。
class Solution(object):
def PredictTheWinner(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""
def getScore(nums, l, r):
if l == r:
return nums[l]
return max(nums[l]-getScore(nums, l+1, r), nums[r]-getScore(nums, l, r-1))
return getScore(nums, 0, len(nums)-1) >= 0改成计划递归，去除重复问题。
class Solution(object):
def PredictTheWinner(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""
dp = collections.defaultdict(list)
def getScore(nums, l, r):
if l == r:
return nums[l]
k = l*len(nums) + r
if dp[k]: # k存的是范围l,r
return dp[k]
dp[k] = max(nums[l]-getScore(nums, l+1, r), nums[r]-getScore(nums, l, r-1))
return dp[k]
return getScore(nums, 0, len(nums)-1) >= 0392. Is Subsequence
跟之前的一题一样的思路。
class Solution(object):
def isSubsequence(self, s, t):
"""
:type s: str
:type t: str
:rtype: bool
"""
search = dict()
for i, v in enumerate(list(t)):
if not search.get(v):
search[v] = [i]
else:
search[v].append(i)
point = 0
for c in s:
if not search.get(c):
return False
ids = search.get(c)
prePoint = point
for i in ids:
if i >= point:
point = i+1
break
if prePoint != point:
prePoint = point
else:
return False
return True494. Target Sum DP
这题思路一开始倒是很简单，关键是索引的处理问题真是要让人发疯。因为数组的索引必须从0开始，不能有负数，所以要加上偏移量。
You are given a list of non-negative integers, a1, a2, ..., an, and a target, S. Now you have 2 symbols + and -. For each integer, you should choose one from + and - as its new symbol.
Find out how many ways to assign symbols to make sum of integers equal to target S.
Example 1:
Input: nums is [1, 1, 1, 1, 1], S is 3.
Output: 5
Explanation:
-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3
There are 5 ways to assign symbols to make the sum of nums be target 3.class Solution(object):
def findTargetSumWays(self, nums, S):
if not nums:
return 0
dic = {nums[0]: 1, -nums[0]: 1} if nums[0] != 0 else {0: 2}
for i in range(1, len(nums)):
tdic = {}
for d in dic:
tdic[d + nums[i]] = tdic.get(d + nums[i], 0) + dic.get(d, 0)
tdic[d - nums[i]] = tdic.get(d - nums[i], 0) + dic.get(d, 0)
dic = tdic
return dic.get(S, 0)自己写的，通过了但是运行时间很长。
class Solution(object):
def findTargetSumWays(self, nums, S):
re = 0
q = [0]
while q:
next_layer = []
ele = nums.pop(0)
for Sum in q:
next_layer += [Sum+ele, Sum-ele]
q = next_layer
if not nums:
break
for s in q:
if s == S:
re += 1
return re740. Delete and Earn
DP
Given an array nums of integers, you can perform operations on the array.
In each operation, you pick any nums[i] and delete it to earn nums[i] points. After, you must delete every element equal to nums[i] - 1 or nums[i] + 1.
You start with 0 points. Return the maximum number of points you can earn by applying such operations.
Example 1:
Input: nums = [3, 4, 2]
Output: 6
Explanation:
Delete 4 to earn 4 points, consequently 3 is also deleted.
Then, delete 2 to earn 2 points. 6 total points are earned.
Example 2:
Input: nums = [2, 2, 3, 3, 3, 4]
Output: 9
Explanation:
Delete 3 to earn 3 points, deleting both 2's and the 4.
Then, delete 3 again to earn 3 points, and 3 again to earn 3 points.
9 total points are earned.思路：
-
If we sort all the numbers into
bucketsindexed by these numbers, this is essentially asking you to repetitively take an bucket while giving up the 2 buckets next to it. (the range of these numbers is [1, 10000]) -
The optimal final result can be derived by keep updating 2 variables
skip_i,take_i, which stands for:skip_i: the best result for sub-problem of first(i+1)buckets from0toi, while you skip theith bucket.take_i: the best result for sub-problem of first(i+1)buckets from0toi, while you take theith bucket. -
DP formula:
take[i] = skip[i-1] + values[i];skip[i] = Math.max(skip[i-1], take[i-1]);take[i]can only be derived from: if you skipped the[i-1]th bucket, and you take bucket[i].skip[i]through, can be derived from eithertake[i-1]orskip[i-1], whatever the bigger;
/**
* for numbers from [1 - 10000], each has a total sum sums[i]; if you earn sums[i], you cannot earn sums[i-1] and sums[i+1]
* kind of like house robbing. you cannot rob 2 connected houses.
*
*/class Solution(object):
def deleteAndEarn(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
if not nums:
return 0
nums = sorted(nums)
sum_num = dict()
for n in nums:
if not sum_num.get(n):
sum_num[n] = n
else:
sum_num[n] += n
length = nums[-1]
take, skip = [0 for i in xrange(length+1)], [0 for i in xrange(length+1)]
take[0] = skip[0] = 0
for i in xrange(1, length+1):
take[i] = skip[i-1] + sum_num[i] if i in nums else skip[i-1]
skip[i] = max(take[i-1], skip[i-1])
return max(take[length], skip[length])377. Combination Sum IV
DP DFS 回溯
回溯很脑残但是超过时间限制
Given an integer array with all positive numbers and no duplicates, find the number of possible combinations that add up to a positive integer target.
Example:
nums = [1, 2, 3]
target = 4
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.
Therefore the output is 7.
Follow up:
What if negative numbers are allowed in the given array?
How does it change the problem?
What limitation we need to add to the question to allow negative numbers?
class Solution(object):
def combinationSum4(self, nums, target):
res = []
self.helper(res, [], target, nums)
return len(res)
def helper(self, res, cur, target, nums):
if target < 0:
return
if target == 0:
res.append(cur)
return
for i in xrange(len(nums)):
self.helper(res, cur+[nums[i]], target-nums[i], nums[:])class Solution(object):
def combinationSum4(self, nums, target):
dp = [0] * (target+1) # dp[target] = sum(dp[target-n]) target有几种
nums = sorted(nums)
dp[0] = 1 # 当target 和 nums[i] 相等时， 只需要Nums[i]1个就可以构成target所以是1
for t in xrange(1, target+1):
count = 0
for n in nums:
if n > t:
break
dp[t] += dp[t-n] # target t 可以从 t-n + n 得到
return dp[target]96. Unique Binary Search Trees
https://www.youtube.com/watch?v=ZAq5BoTes8o
Given n, how many structurally unique BST's (binary search trees) that store values 1 ... n?
Example:
Input: 3
Output: 5
Explanation:
Given n = 3, there are a total of 5 unique BST's:
1 3 3 2 1
\ / / / \ \
3 2 1 1 3 2
/ / \ \
2 1 2 3
class Solution(object):
def numTrees(self, n):
dp = [0 for i in xrange(n+1)]
dp[0] = dp[1] = 1
for i in xrange(2, n+1):
s = 0
for j in xrange(0, i):
s += dp[j] * dp[i-1-j]
dp[i] = s
return dp[i]300. Longest Increasing Subsequence
DP 算法课的经典题
Given an unsorted array of integers, find the length of longest increasing subsequence.
Example:
Input:[10,9,2,5,3,7,101,18]Output: 4 Explanation: The longest increasing subsequence is[2,3,7,101], therefore the length is4.
Note:
- There may be more than one LIS combination, it is only necessary for you to return the length.
- Your algorithm should run in O(n2) complexity.
class Solution(object):
def lengthOfLIS(self, nums):
if not nums:
return 0
dp = [0 for i in nums]
dp[0] = 1
res = 1
for i in xrange(1, len(nums)):
longest = 0
for j in xrange(0, i):
if nums[j] < nums[i]:
longest = max(longest, dp[j])
dp[i] = longest + 1
res = max(res, dp[i])
return res646. Maximum Length of Pair Chain
DP 和上题最长递增子数列一样的
You are given n pairs of numbers. In every pair, the first number is always smaller than the second number.
Now, we define a pair (c, d) can follow another pair (a, b) if and only if b < c. Chain of pairs can be formed in this fashion.
Given a set of pairs, find the length longest chain which can be formed. You needn't use up all the given pairs. You can select pairs in any order.
Example 1:
Input: [[1,2], [2,3], [3,4]]
Output: 2
Explanation: The longest chain is [1,2] -> [3,4]class Solution(object):
def findLongestChain(self, pairs):
if not pairs:
return 0
pairs = sorted(pairs)
dp = [1 for i in pairs]
res = 1
for i in xrange(1, len(pairs)):
longest = 0
for j in xrange(i):
if pairs[j][1] < pairs[i][0]:
longest = max(longest, dp[j])
dp[i] = longest + 1
res = max(res, dp[i])
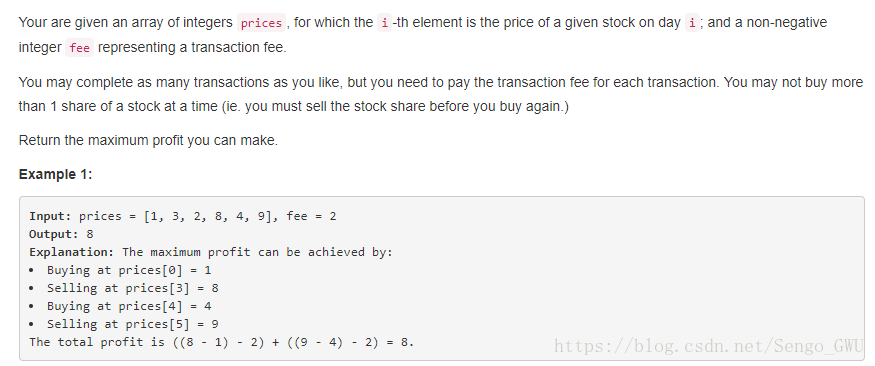
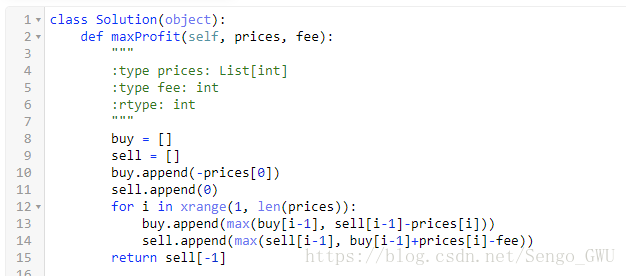
return res714. Best Time to Buy and Sell Stock with Transaction Fee
关键
DP
309. Best Time to Buy and Sell Stock with Cooldown
DP 和上一题一样的思路
Say you have an array for which the ith element is the price of a given stock on day i.
Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times) with the following restrictions:
- You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
- After you sell your stock, you cannot buy stock on next day. (ie, cooldown 1 day)
Example:
Input: [1,2,3,0,2]
Output: 3
Explanation: transactions = [buy, sell, cooldown, buy, sell]class Solution(object):
def maxProfit(self, prices):
if len(prices) < 2:
return 0
buy, sell = [0 for i in prices], [0 for i in prices]
buy[0] = -prices[0]
buy[1] = -min(prices[0], prices[1])
sell[0], sell[1] = 0, max(prices[1]-prices[0], 0)
for i in xrange(2, len(prices)):
buy[i] = max(sell[i-2]-prices[i], buy[i-1])
sell[i] = max(buy[i-1]+prices[i], sell[i-1])
return max(sell[-1], 0)
reduce the O(n) space to O(1).
def maxProfit(self, prices):
if len(prices) < 2:
return 0
sell, buy, prev_sell, prev_buy = 0, -prices[0], 0, 0
for price in prices:
prev_buy = buy
buy = max(prev_sell - price, prev_buy)
prev_sell = sell
sell = max(prev_buy + price, prev_sell)
return sell 279. Perfect Squares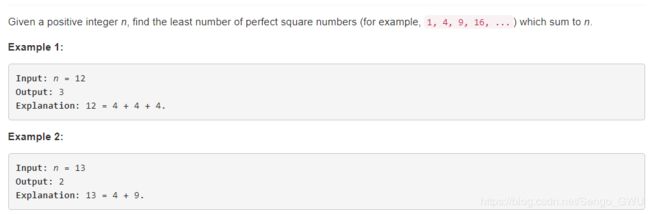
BFS
class Solution(object):
def numSquares(self, n):
square = [i*i for i in xrange(1, int(math.sqrt(n))+1)]
curLevel = [0]
l = 0
while True:
nextLevel = []
for a in curLevel:
for b in square:
if a + b == n:
return l + 1 # Found n with min level
if a + b < n:
nextLevel.append(a+b)
curLevel = set(nextLevel)
l += 1DP:
dp[n] indicates that the perfect squares count of the given n, and we have:
dp[0] = 0
dp[1] = dp[0]+1 = 1
dp[2] = dp[1]+1 = 2
dp[3] = dp[2]+1 = 3
dp[4] = Min{ dp[4-1*1]+1, dp[4-2*2]+1 }
= Min{ dp[3]+1, dp[0]+1 }
= 1
dp[5] = Min{ dp[5-1*1]+1, dp[5-2*2]+1 }
= Min{ dp[4]+1, dp[1]+1 }
= 2
.
.
.
dp[13] = Min{ dp[13-1*1]+1, dp[13-2*2]+1, dp[13-3*3]+1 }
= Min{ dp[12]+1, dp[9]+1, dp[4]+1 }
= 2
.
.
.
dp[n] = Min{ dp[n - i*i] + 1 }, n - i*i >=0 && i >= 1
class Solution(object):
def numSquares(self, n):
dp = [float('inf') for i in xrange(n+1)]
dp[0] = 0
for i in xrange(1, n+1):
for j in xrange(1, i+1):
if j*j > i:
break
else:
dp[i] = min(dp[i], dp[i-j*j]+1)
return dp[n]376. Wiggle Subsequence
A sequence of numbers is called a wiggle sequence if the differences between successive numbers strictly alternate between positive and negative. The first difference (if one exists) may be either positive or negative. A sequence with fewer than two elements is trivially a wiggle sequence.
For example, [1,7,4,9,2,5] is a wiggle sequence because the differences (6,-3,5,-7,3) are alternately positive and negative. In contrast, [1,4,7,2,5] and [1,7,4,5,5] are not wiggle sequences, the first because its first two differences are positive and the second because its last difference is zero.
Given a sequence of integers, return the length of the longest subsequence that is a wiggle sequence. A subsequence is obtained by deleting some number of elements (eventually, also zero) from the original sequence, leaving the remaining elements in their original order.
Examples:
Input: [1,7,4,9,2,5]
Output: 6
The entire sequence is a wiggle sequence.
Input: [1,17,5,10,13,15,10,5,16,8]
Output: 7
There are several subsequences that achieve this length. One is [1,17,10,13,10,16,8].
Input: [1,2,3,4,5,6,7,8,9]
Output: 2
Follow up:
Can you do it in O(n) time?
class Solution(object):
def wiggleMaxLength(self, nums):
if not nums:
return 0
up, down = [0 for i in xrange(len(nums))], [0 for i in xrange(len(nums))]
up[0] = down[0] = 1
for i in xrange(1, len(nums)):
if nums[i] > nums[i-1]:
up[i] = down[i-1] + 1
down[i] = down[i-1]
elif nums[i] < nums[i-1]:
down[i] = up[i-1] + 1
up[i] = up[i-1]
else:
down[i] = down[i-1]
up[i] = up[i-1]
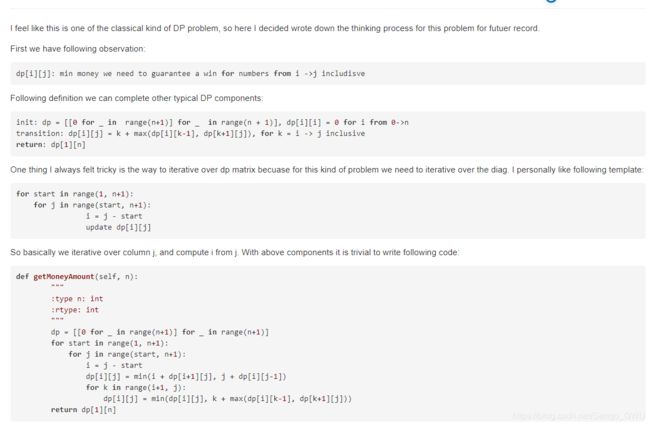
return max(down[-1], up[-1])375. Guess Number Higher or Lower II
思路：方案最佳，运气最坏。
Definition of dp[i][j]: minimum number of money to guarantee win for subproblem [i, j].
Target: dp[1][n]
Corner case: dp[i][i] = 0 (because the only element must be correct)
Equation: we can choose k (i<=k<=j) as our guess, and pay price k. After our guess, the problem is divided into two subproblems. Notice we do not need to pay the money for both subproblems. We only need to pay the worst case (because the system will tell us which side we should go) to guarantee win. So dp[i][j] = min (i<=k<=j) { k + max(dp[i][k-1], dp[k+1][j]) }
每一步找到的使得cost最小的K就是最佳方案，而后面的 max(dp[low][k-1], dp[k+1][high])就是最坏情况。
class Solution(object):
def getMoneyAmount(self, n):
"""
:type n: int
:rtype: int
"""
dp = [[0]*(n+1) for i in xrange(n+1)]
for low in xrange(n, 0, -1):
for high in xrange(low, n+1):
if low == high:
dp[low][high] = 0
continue
cost = float('inf')
for k in xrange(low, high+1):
if k == low: # k == low 时候，最坏情况答案在另外一侧
cost = min(cost, k+dp[k+1][high])
elif k == high: # k == high
cost = min(cost, k+dp[low][k-1])
else:
cost = min(cost, k + max(dp[low][k-1], dp[k+1][high]))
dp[low][high] = cost
return dp[1][n]
https://leetcode.com/problems/guess-number-higher-or-lower-ii/discuss/156018/Python-solution-with-explanation
384. Shuffle an Array
打乱数组
class Solution(object):
def __init__(self, nums):
"""
:type nums: List[int]
"""
self.nums = nums
def reset(self):
"""
Resets the array to its original configuration and return it.
:rtype: List[int]
"""
return self.nums
def shuffle(self):
"""
Returns a random shuffling of the array.
:rtype: List[int]
"""
res = self.nums[:]
for i in xrange(len(res)-1, 0, -1):
j = random.randint(0, i)
res[i], res[j] = res[j], res[i]
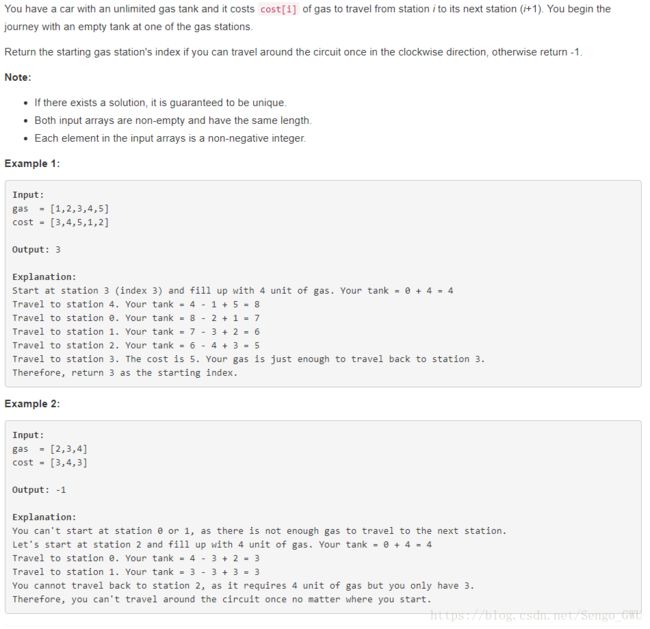
return res134. Gas Station
- If car starts at A and can not reach B. Any station between A and B
can not reach B.(B is the first station that A can not reach.) - If the total number of gas is bigger than the total number of cost. There must be a solution.
class Solution(object):
def canCompleteCircuit(self, gas, cost):
tank = begin = total= 0
for i in xrange(len(gas)):
tank += gas[i] - cost[i]
if tank < 0:
begin = i + 1
total += tank
tank = 0
if tank + total >= 0:
return begin
else:
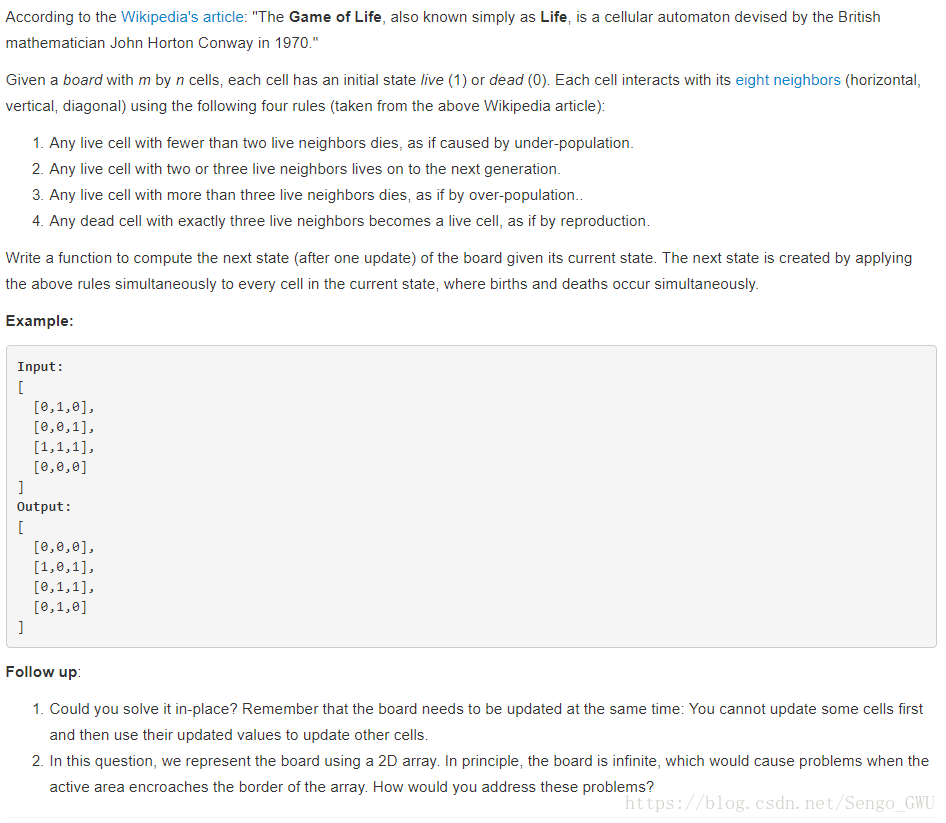
return -1289. Game of Life
class Solution(object):
def gameOfLife(self, board):
"""
:type board: List[List[int]]
:rtype: void Do not return anything, modify board in-place instead.
"""
changeList = set()
def judge(i, j, board, changeList):
live = 0
for x, y in ((i + 1, j), (i - 1, j), (i, j + 1), (i, j - 1), (i - 1, j - 1), (i - 1, j + 1), (i + 1, j - 1),
(i + 1, j + 1)):
if 0 <= x < len(board) and 0 <= y < len(board[0]) and board[x][y] == 1:
live += 1
if live < 2 and board[i][j] == 1:
changeList.add((i, j))
elif live > 3 and board[i][j] == 1:
changeList.add((i, j))
elif live == 3 and board[i][j] == 0:
changeList.add((i, j))
for i in xrange(len(board)):
for j in xrange(len(board[0])):
judge(i, j, board, changeList)
for pair in changeList:
x, y = pair
board[x][y] = 0 if board[x][y] else 1689. Maximum Sum of 3 Non-Overlapping Subarrays
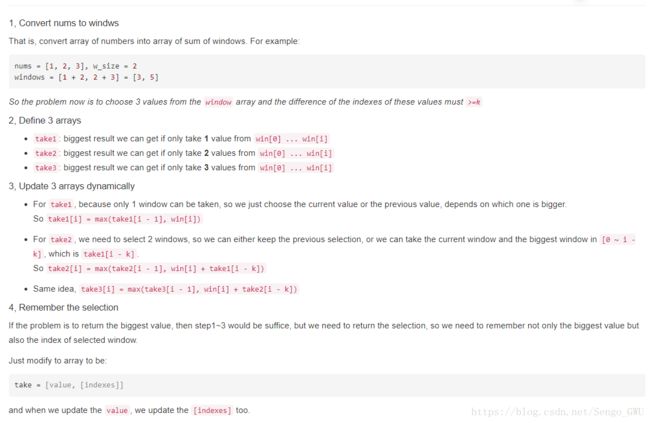https://leetcode.com/problems/maximum-sum-of-3-non-overlapping-subarrays/discuss/166159/Python-Easy-to-Understand-O(n)-Solution-using-DP
class Solution(object):
def maxSumOfThreeSubarrays(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: List[int]
"""
subsum = sum(nums[:k])
take1 = [(0, ()) for _ in range(len(nums))]
take2 = [(0, ()) for _ in range(len(nums))]
take3 = [(0, ()) for _ in range(len(nums))]
for i in xrange(k-1, len(nums)):
if i != k - 1:
subsum = subsum - nums[i - k] + nums[i]
# update take1
if subsum > take1[i-1][0]:
take1[i] = (subsum, (i - k + 1,))
else:
take1[i] = take1[i-1]
# update take2
if subsum + take1[i-k][0] > take2[i-1][0]:
newVal = subsum + take1[i-k][0]
newIdx = take1[i-k][1] + (i - k + 1, )
take2[i] = (newVal, newIdx)
else:
take2[i] = take2[i-1]
# update take3
if subsum + take2[i-k][0] > take3[i-1][0]:
newVal = subsum + take2[i-k][0]
newIdx = take2[i-k][1] + (i - k + 1, )
take3[i] = (newVal, newIdx)
else:
take3[i] = take3[i-1]
return take3[-1][-1]
277. Find the Celebrity
# The knows API is already defined for you.
# @param a, person a
# @param b, person b
# @return a boolean, whether a knows b
# def knows(a, b):
class Solution(object):
def findCelebrity(self, n):
"""
:type n: int
:rtype: int
"""
x = 0
for i in xrange(n): # After the first loop, x is the only candidate.
if knows(x, i):
x = i
# 验证x是不是名人
if any(knows(x, i) for i in xrange(n) if i != x):
return -1
if all(knows(i, x) for i in xrange(n) if i != x):
return x
return -1