计算智能 蚁群算法

一.概念介绍

蚁群算法是自然界蚂蚁的寻径方式进行模拟而得出的一种仿生算法：在蚂蚁运动过程中，能够在它所经过的路径上留下信息素的物质进行信息传递，而且蚂蚁在运行过程中能够感知这种物质，并以此指导自己的运动方向。

由大量蚂蚁组成的蚁群集体行为便表现出一种信息正反馈现象：某一路径上走过的蚂蚁越多，则后来者选择该路径的概率就越大

二.基本原理

1、蚂蚁在路径上释放信息素。

2、碰到还没走过的路口，就随机挑选一条路走。同时，释放与路径长度有关的信息素。

3、信息素浓度与路径长度成反比。后来的蚂蚁再次碰到该路口时，就选择信息素浓度较高路径。

4、最优路径上的信息素浓度越来越大。

5、最终蚁群找到最优寻食路径。

二.基本步骤

1.路径构建

对于每只蚂蚁k，路径记忆向量 按照访问顺序记录了所有k已经经过的城市序号。设蚂蚁k当前所在城市为i，
则其选择城市j作为下一个访问对象的概率为：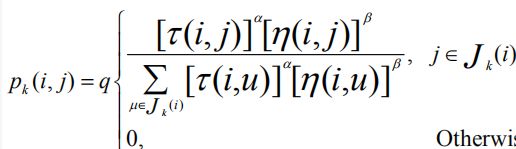

2.信息素更新

m是蚂蚁个数, ρ是信息素的蒸发率，规定0≤ ρ≤1，在AS中通常设置为 ρ =0.5，Δτij是第k只蚂蚁在它经过的边上释放的信息素量，它等于蚂蚁k本轮构建路径长度的倒数。Ck表示路径长度，它是Rk中所有边的长度和。

算法流程：

 

三.蚁群算法中相关参数介绍（设计参数的原因会通过实验来验证）

蚂蚁数量： 
设m表示蚂蚁数量。m的数量很重要，因为m过大时，会导致搜索过的路径上信息素变化趋于平均，这样就不好找出好的路径了；m过小时，易使未被搜索到的路径信息素减小到0，这样可能会出现早熟，没找到全局最优解。一般上，在时间等资源条件紧迫的情况下，蚂蚁数设定为城市数的1.5倍较稳妥。

信息素因子： 
信息素因子反映了蚂蚁在移动过程中所积累的信息量在指导蚁群搜索中的相对重要程度，其值过大，蚂蚁选择以前走过的路径概率大，搜索随机性减弱；值过小，等同于贪婪算法，使搜索过早陷入局部最优。实验发现，信息素因子选择[1,5]区间，性能较好。

启发函数因子： 
启发函数因子反映了启发式信息在指导蚁群搜索过程中的相对重要程度，其大小反映的是蚁群寻优过程中先验性和确定性因素的作用强度。过大时，虽然收敛速度会加快，但容易陷入局部最优；过小时，容易陷入随机搜索，找不到最优解。实验发现，当启发函数因子为[3,5]时，综合求解性能较好。

信息素挥发因子： 
信息素挥发因子表示信息素的消失水平，它的大小直接关系到蚁群算法的全局搜索能力和收敛速度。实验发现，当属于[0.2，0.5]时,综合性能较好。

信息素常数： 
这个参数为信息素强度，表示蚂蚁循环一周时释放在路径上的信息素总量，其作用是为了充分利用有向图上的全局信息反馈量，使算法在正反馈机制作用下以合理的演化速度搜索到全局最优解。值越大，蚂蚁在已遍历路径上的信息素积累越快，有助于快速收敛。实验发现，当值属于[10,1000]时，综合性能较好。

最大迭代次数： 
最大迭代次数值过小，可能导致算法还没收敛就已结束；过大则会导致资源浪费。一般最大迭代次数可以取100到500次。一般来讲，建议先取200，然后根据执行程序查看算法收敛的轨迹来修改取值。

四.利用蚁群算法解决TSP问题实例

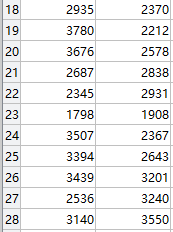
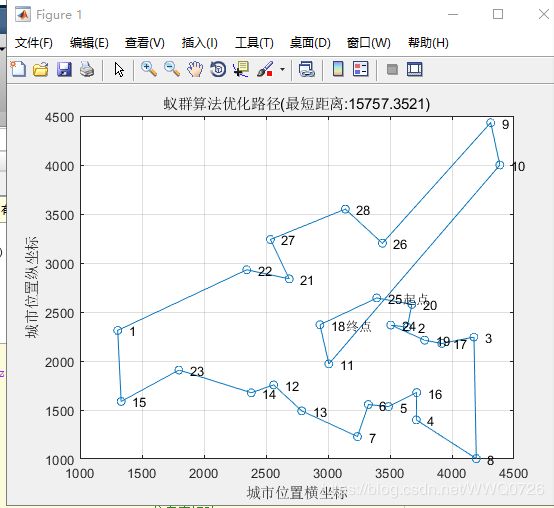
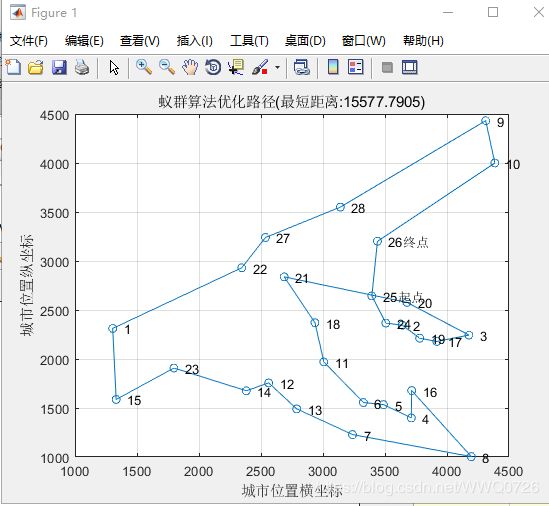
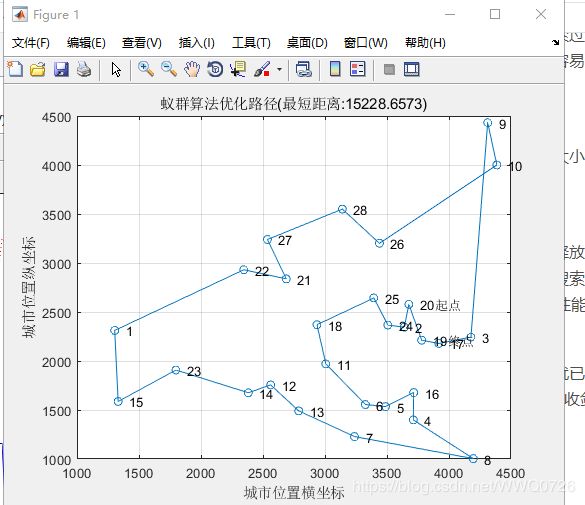
我解决的问题是28个城市的TSP：

首先初始化城市序列 如下图所示

       

 

 

其次，初始化相关参数

%% 初始化参数
fprintf('Initializing Parameters... \n');
m = 50;                              % 蚂蚁数量
alpha = 1;                           % 信息素重要程度因子
beta = 5;                            % 启发函数重要程度因子
rho = 0.1;                           % 信息素挥发因子
Q = 1;                               % 常系数
Eta = 1./D;                          % 启发函数
Tau = ones(n,n);                     % 信息素矩阵
Table = zeros(m,n);                  % 路径记录表
iter = 1;                            % 迭代次数初值
iter_max = 150;                      % 最大迭代次数
Route_best = zeros(iter_max,n);      % 各代最佳路径       
Length_best = zeros(iter_max,1);     % 各代最佳路径的长度  
Length_ave = zeros(iter_max,1);      % 各代路径的平均长度  

计算城市间距离

%% 导入数据
load cimat

tys_data.%% 计算城市间相互距离
fprintf('Computing Distance Matrix... \n');
n = size(citys,1);
D = zeros(n,n);
for i = 1:n
    for j = 1:n
        if i ~= j
            D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));
        else
            D(i,j) = 1e-4;      
        end
    end    
end

下面就可以进入迭代 ，我选择一般情况下比较合适的迭代次数150次

%% 迭代寻找最佳路径
figure;
while iter <= iter_max
    fprintf('迭代第%d次\n',iter);
    % 随机产生各个蚂蚁的起点城市
      start = zeros(m,1);
      for i = 1:m
          temp = randperm(n);
          start(i) = temp(1);
      end
      Table(:,1) = start;
      % 构建解空间
      citys_index = 1:n;
      % 逐个蚂蚁路径选择
      for i = 1:m
          % 逐个城市路径选择
         for j = 2:n
             tabu = Table(i,1:(j - 1));           % 已访问的城市集合(禁忌表)
             allow_index = ~ismember(citys_index,tabu);
             allow = citys_index(allow_index);  % 待访问的城市集合
             P = allow;
             % 计算城市间转移概率
             for k = 1:length(allow)
                 P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta;
             end
             P = P/sum(P);
             % 轮盘赌法选择下一个访问城市
             Pc = cumsum(P);     
            target_index = find(Pc >= rand);
            target = allow(target_index(1));
            Table(i,j) = target;
         end
      end
      % 计算各个蚂蚁的路径距离
      Length = zeros(m,1);
      for i = 1:m
          Route = Table(i,:);
          for j = 1:(n - 1)
              Length(i) = Length(i) + D(Route(j),Route(j + 1));
          end
          Length(i) = Length(i) + D(Route(n),Route(1));
      end
      % 计算最短路径距离及平均距离
      if iter == 1
          [min_Length,min_index] = min(Length);
          Length_best(iter) = min_Length;  
          Length_ave(iter) = mean(Length);
          Route_best(iter,:) = Table(min_index,:);
      else
          [min_Length,min_index] = min(Length);
          Length_best(iter) = min(Length_best(iter - 1),min_Length);
          Length_ave(iter) = mean(Length);
          if Length_best(iter) == min_Length
              Route_best(iter,:) = Table(min_index,:);
          else
              Route_best(iter,:) = Route_best((iter-1),:);
          end
      end
      % 更新信息素
      Delta_Tau = zeros(n,n);
      % 逐个蚂蚁计算
      for i = 1:m
          % 逐个城市计算
          for j = 1:(n - 1)
              Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i);
          end
          Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i);
      end
      Tau = (1-rho) * Tau + Delta_Tau;
    % 迭代次数加1，清空路径记录表

 %   figure;
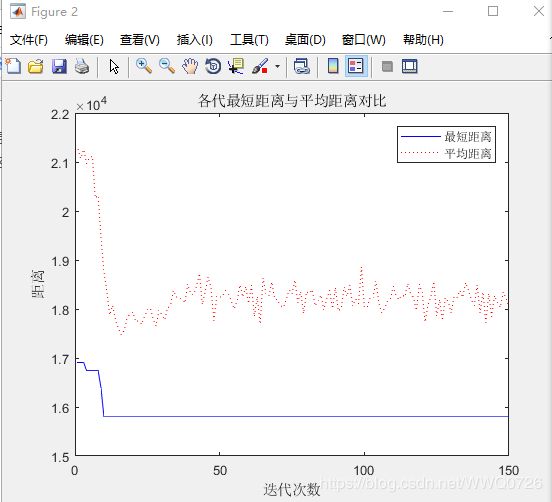
 %最佳路径的迭代变化过程
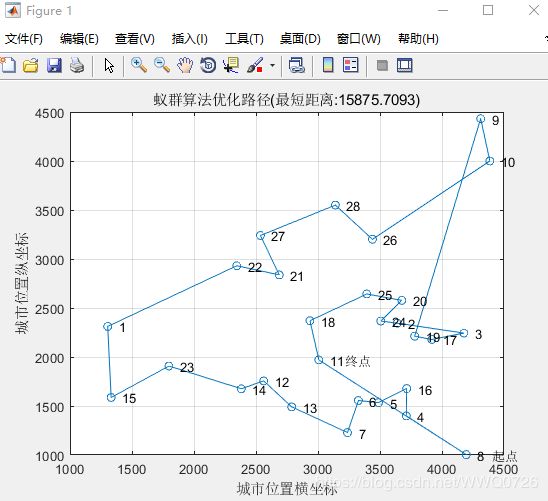
    [Shortest_Length,index] = min(Length_best(1:iter));
    Shortest_Route = Route_best(index,:);
    plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
    [citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
    pause(0.3);
 
    iter = iter + 1;
    Table = zeros(m,n);

 % end
end

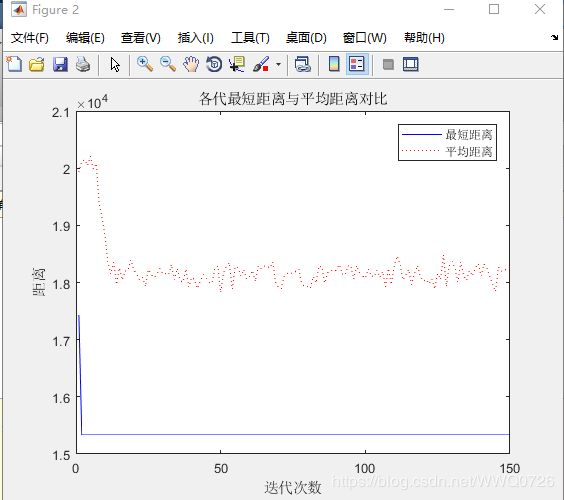
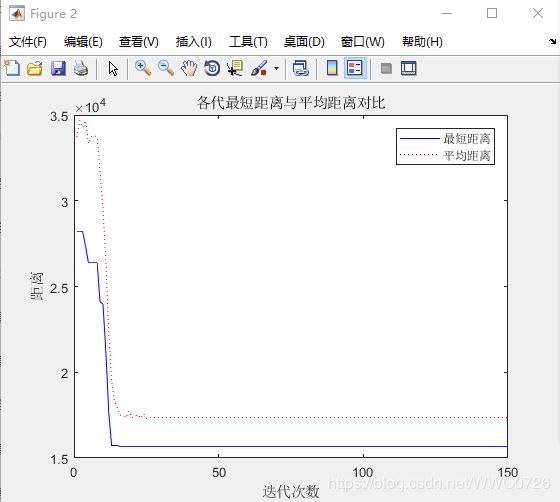
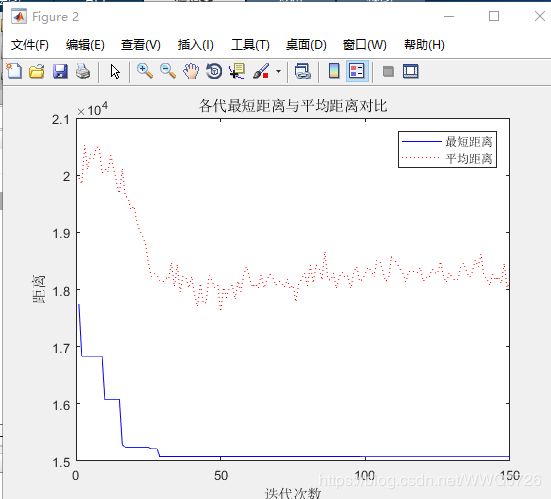
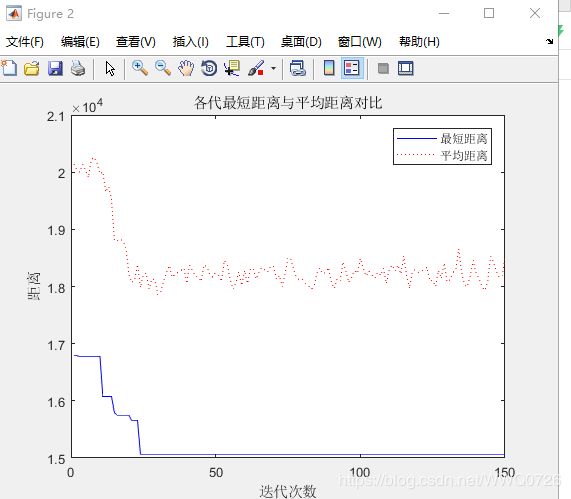
最终结果

四.验证参数alpha，.beta，rho 对算法的影响

alpha变化，beta=5,rho=0.1

1.alpha = 2;                           % 信息素重要程度因子

2.alpha=3

3.alpha=4

4.alpha=5

小结：通过增大信息素重要程度因子，发现其最优路径都比我初始设置的1要大，可见信息素重要程度因子值过大，蚂蚁选择以前走过的路径概率大，搜索随机性减弱；值过小，等同于贪婪算法，使搜索过早陷入局部最优。

beta改变，alpha,rho不变

1.beta = 1;                            % 启发函数重要程度因子

2.beta=2

3.beta=3

4.beta=4

 

小结：增大启发函数重要程度因子可以发现当其值越大，蚁群就容易选择局部最优路径，算法的收敛速度加快，但是随机性不高，容易得到局部的最优解。

.rho改变，alpha,beta不变                       

1.rho=0.1

2.rho=0.2

3.rho=0.3

4.rho=0.4

小结：增大信息挥发因子，可以发现易于找到最短距离，收敛速度加快，而且当其值过小，其收敛速度比较慢，因为信息素挥发比较慢，就比较容易集中局部最优的路径，收敛速度也会比较慢。

五.结论

信息素重要程度因子选择[1,5]区间，启发函数重要程度因子为[3,5]时，信息素挥发因子[0.2，0.5]时,综合性能较好。就我的本次实验来看，信息素重要程度为1，启发函数重要程度因子为5，信息素挥发因子为0.5时，综合效果最优。其次，通过实验也发现了蚁群算法的一些缺点：①易于陷入局部最优，②迭代次数比较多