蚁群算法|4.5

---

蚁群算法

---

以下内容来源于参考文献，仅供学习交流。

一、什么是蚁群算法

蚁群算法是一种用来寻找优化路径的概率型算法。它由Marco Dorigo于1992年在他的博士论文中提出，其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。

二、蚁群算法的来源及背景

蚁群算法是意大利学者Dorigo、Maniezzo等人于20世纪90年代看蚂蚁觅食发明的。这意大利的大兄弟在看蚂蚁觅食的时候呢，发现单个蚂蚁的行为比较简单，但是蚂蚁群却能体现一些智能行为，比如蚂蚁能在不同环境中，寻找最短的从蚂蚁窝到达食物的路径。经过进一步研究发现，蚂蚁在找食物的路径会留下记号（生物学称之为“信息素”），蚂蚁群里的蚂蚁会根据这个记号，也就是信息素行走，每个蚂蚁都做记号，经过一段时间后，整个蚂蚁群就会找到一个最短的到达食物的路径了。

三、蚁群算法的用途

该算法应用于其他组合优化问题，如旅行商问题、指派问题、Job—shop调度问题、车辆路由问题、图着色问题和网络路由问题等。最近几年，该算法在网络路由中的应用受到越来越多学者的关注，并提出了一些新的基于蚂蚁算法的路由算法。同传统的路由算法相比较，该算法在网络路由中具有信息分布式性、动态性、随机性和异步性等特点，而这些特点正好能满足网络路由的需要。

四、人工蚂蚁和真实蚂蚁的异同

同：
（1）都是一群相互协作的个体。与真实蚁群一样，蚁群算法由一群人工蚂蚁组成，人工蚂蚁之间通过同步/异步协作来寻找问题的最优解。虽然单只人工蚂蚁可以构造出问题的解，但只有当多只人工蚂蚁通过相互协作，才能发现问题的最优（次优）解。人工蚂蚁个体间通过写/读问题的状态变量来进行协作。
2）如真实蚂蚁一样，人工蚂蚁通过改变所访问过的问题的数字状态信息来进行协作。另外，蚁群算法还用到了蒸发机制，这一点对应于真实蚂蚁中信息素的蒸发现象。蒸发机制使蚁群逐渐忘记过去的历史，从而更好地指导蚂蚁的搜索方向。
3）人工蚂蚁和真实蚂蚁都按照概率决策规则从一种状态转移到另一种相邻状态。其中的概率决策规则是与问题相关的信息和局部环境信息的函数。在状态转移过程中，人工蚂蚁和真实蚂蚁都只用到了局部信息，没有使用前瞻策略来预见将来的状态。

异：
（1）人工蚂蚁生活在离散的时间，从一种离散状态到另一种离散状态。（2）人工蚂蚁具有内部状态，即人工蚂蚁具有一定的记忆能力，能记住自己走过的地方。
（3）人工蚂蚁释放信息素的数量是其生成解的质量的函数。
（4）人工蚂蚁更新信息素的时机依赖于特定的问题。例如，大多数人工蚂蚁仅仅在其找到一个解之后才更新路径上的信息素。

五、蚁群算法的优点

（1）蚁群算法是一种本质上的并行算法
（2）蚁群算法是一种自组织的算法。
（3）蚁群算法具有较强的鲁棒性。
（4）蚁群算法是一种正反馈算法。

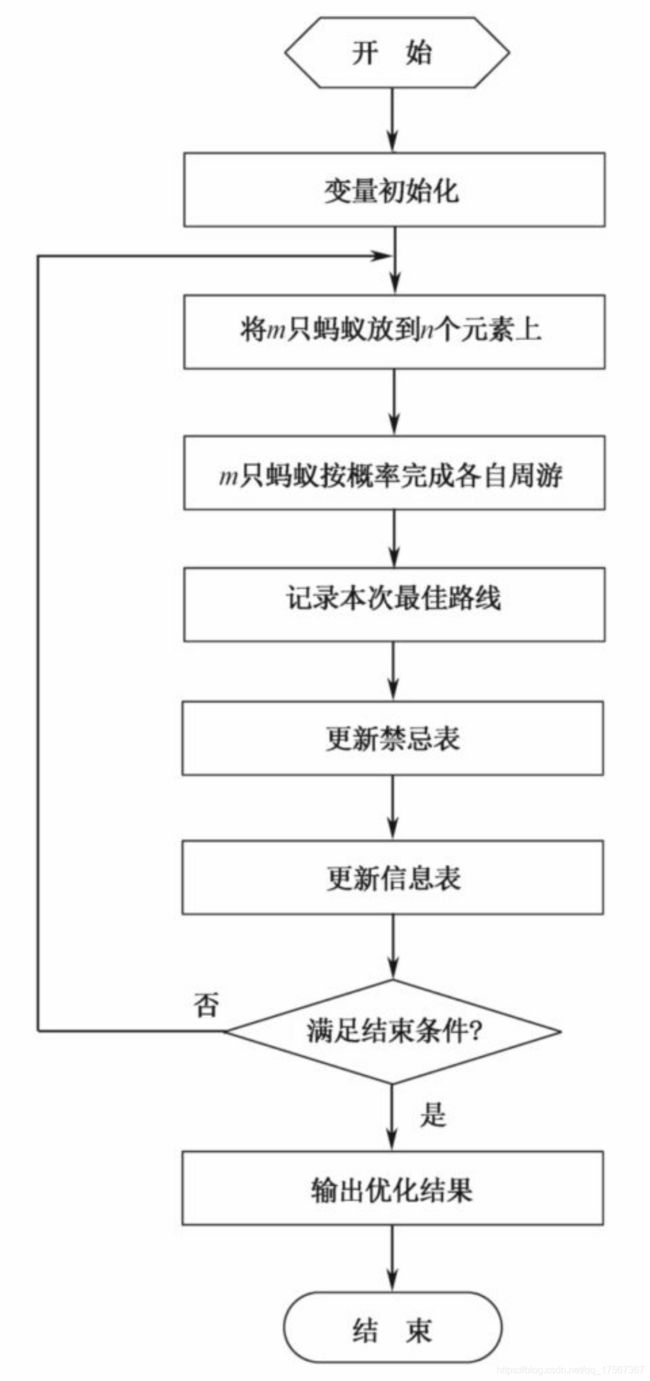
六、蚁群算法的步骤及实现

（1）参数初始化。令时间t=0和循环次数Nc=0，设置最大循环次数G，将m个蚂蚁置于n个元素（城市）上，令有向图上每条边（i，j）的初始化信息量τij（t）=c，其中c表示常数，且初始时刻Δτij（0）=0。
（2）循环次数Nc=Nc+1。
（3）蚂蚁的禁忌表索引号k=1。
（4）蚂蚁数目k=k+1。
（5）蚂蚁个体根据状态转移概率公式（5.1）计算的概率选择元素j并前进，j∈｛Jk（i）｝。
（6）修改禁忌表指针，即选择好之后将蚂蚁移动到新的元素，并把该元素移动到该蚂蚁个体的禁忌表中。
（7）若集合C中元素未遍历完，即k＜m，则跳转到第（4）步；否则，执行第（8）步。
（8）记录本次最佳路线。
（9）根据式（5.2）和式（5.3）更新每条路径上的信息量。
（10）若满足结束条件，即如果循环次数Nc≥G，则循环结束并输出程序优化结果；否则清空禁忌表并跳转到第（2）步。

function[R_best,L_best,L_ave,Shortest_Route,Shortest_Length]=ACATSP(C,NC_max,m,Alpha,Beta,Rho,Q)

%第一步
n=size(C,1);
D=zeros(n,n);
for i=1:n
for j=1:n
    if i~=j
        
            D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)*0.5;
    else
            D(i,j)=eps;
    end

    D(j,i)=D(i,j);
end  
end 
Eta=1./D;
Tau=ones(n,n);
Tabu=zeros(m,n);
NC=1;
R_best=zeros(NC_max,n);
L_best=inf.*ones(NC_max,1);
L_ave=zeros(NC_max,1);
while NC<=NC_max
%第二步
    Randpos=[];
    for i=1:(ceil(m/n))
        Randpos=[Randpos,randperm(n)];
    end
    Tabu(:,1)=(Randpos(1,1:m))';
%第三步  
    for j=2:n
        for i=1:m
            visited=Tabu(i,1:(j-1));
            J=zeros(1,(n-j+1));
            P=J;
            Jc=1;
            for k=1:n
                if isempty(find(visited==k, 1))
                    J(Jc)=k;
                    Jc=Jc+1;
                end
            end
            for k=1:length(J)
                P(k)=(Tau(visited(end),J(k))^Alpha)*(Eta(visited(end),J(k))^Beta);
            end
            P=P/(sum(P));
            Pcum=cumsum(P);
            Select=find(Pcum>=rand);
            to_visit=J(Select(1));
            Tabu(i,j)=to_visit;
        end
    end
    if NC>=2
        Tabu(1,:)=R_best(NC-1,:);
    end
    
    %第四步
    L=zeros(m,1);
    for i=1:m
        R=Tabu(i,:);
        for j=1:(n-1)
            L(i)=L(i)+D(R(j),R(j+1));
        end
        L(i)=L(i)+D(R(1),R(n));
    end
    L_best(NC)=min(L);
    pos=find(L==L_best(NC));
    R_best(NC,:)=Tabu(pos(1),:);
    L_ave(NC)=mean(L);
    NC=NC+1
    %第五步
    Delta_Tau=zeros(n,n);
    for i=1:m
        for j=1:(n-1)
            Delta_Tau(Tabu(i,j),Tabu(i,j+1))=Delta_Tau(Tabu(i,j),Tabu(i,j+1))+Q/L(i);
            
        end
        Delta_Tau(Tabu(i,n),Tabu(i,1))=Delta_Tau(Tabu(i,n),Tabu(i,1))+Q/L(i);
    end
    Tau=(1-Rho).*Tau+Delta_Tau;

    %第六步禁忌表清0
    Tabu=zeros(m,n);
end
%第七步：输出结果
Pos=find(L_best==min(L_best));
Shortest_Route=R_best(Pos(1),:)
Shortest_Length=L_best(Pos(1))
subplot(1,2,1)
DrawRoute(C,Shortest_Route)
subplot(1,2,2)
plot(L_best)
hold on
plot(L_ave,'r')
title('平均距离和最短距离')



function DrawRoute(C,R)
N=length(R);
scatter(C(:,1),C(:,2));
hold on
plot([C(R(1),1),C(R(N),1)],[C(R(1),2),C(R(N),2)],'g')
hold on
for ii=2:N
    plot([C(R(ii-1),1),C(R(ii),1)],[C(R(ii-1),2),C(R(ii),2)],'g')
    hold on
end
title('旅行商问题优化结果')
       

七、相关参数解释

1.信息素启发式因子α：代表信息量对是否选择当前路径的影响程度，即反映蚂蚁在运动过程中所积累的信息量在指导蚁群搜索中的相对重要程度。α的大小反映了蚁群在路径搜索中随机性因素作用的强度，其值越大，蚂蚁在选择以前走过的路径的可能性就越大，搜索的随机性就会减弱；而当启发式因子α的值过小时，则易使蚁群的搜索过早陷于局部最优。根据经验，信息素启发式因子α取值范围一般为［l，4］时，蚁群算法的综合求解性能较好。

2.期望启发因子β表示在搜索时路径上的信息素在指导蚂蚁选择路径时的向导性，它的大小反映了蚁群在搜索最优路径的过程中的先验性和确定性因素的作用强度。期望启发因子β的值越大，蚂蚁在某个局部点上选择局部最短路径的可能性就越大，虽然这个时候算法的收敛速度得以加快，但蚁群搜索最优路径的随机性减弱，而此时搜索易于陷入局部最优解。根据经验，期望启发因子β取值范围一般为［3，5］，此时蚁群算法的综合求解性能较好。

3.信息素蒸发系数ρ蚁群算法中的人工蚂蚁是具有记忆功能的，随着时间的推移，以前留下的信息素将会逐渐消逝，蚁群算法与其他各种仿生进化算法一样，也存在着收敛速度慢、容易陷入局部最优解等缺陷，而信息素蒸发系数ρ大小的选择将直接影响到整个蚁群算法的收敛速度和全局搜索性能。在蚁群算法的抽象模型中，ρ表示信息素蒸发系数，1-ρ则表示信息素持久性系数。因此，ρ的取值范围应该是0～1之间的一个数，表示信息素的蒸发程度，它实际上反映了蚂蚁群体中个体之间相互影响的强弱。ρ过小时，则表示以前搜索过的路径被再次选择的可能性过大，会影响到算法的随机性能和全局搜索能力；ρ过大时，说明路径上的信息素挥发的相对变多，虽然可以提高算法的随机搜索性能和全局搜索能力，但过多无用搜索操作势必会降低算法的收敛速度。

4.蚂蚁数目m蚁群算法是一种随机搜索算法，与其他模拟进化算法一样，通过多个候选解组成的群体进化过程来寻求最优解，在该过程中不仅需要每个个体的自适应能力，更需要群体之间的相互协作能力。蚁群在搜索过程中之所以表现出复杂有序的行为，是因为个体之间的信息交流与相互协作起着至关重要的作用。

5.最大进化代数G是表示蚁群算法运行结束条件的一个参数，表示蚁群算法运行到指定的进化代数之后就停止运行，并将当前群体中的最佳个体作为所求问题的最优解输出。一般G取100～500。

6.禁忌表：在禁忌搜索算法中，禁忌表是用来防止搜索过程中出现循环，避 免陷入局部最优的。

八、相关文献参考

1.《人工智能算法》
2.《智能优化算法及其MATLAB实例》