数学狂想曲（六）——Gabriel's Horn, 函数连续性

https://antkillerfarm.github.io/

数学的深渊

Gabriel’s Horn

Gabriel’s Horn，又名托里拆利小号（Torricelli’s trumpet），是数学史上非常经典的模型。它最早由Evangelista Torricelli提出，故名。

注：Evangelista Torricelli，1608~1647，意大利物理学家和数学家。主要研究气压、水压，提出了托里拆利原理，并发明了气压计。

上图是Gabriel’s Horn的图像，它由 y=1x(x>1) 绕x轴旋转得到。Torricelli发现Gabriel’s Horn是个体积有限，而表面积无限的形状。

V=π∫1a(1x)2dx=π(1−1a)

lima→∞V=lima→∞π(1−1a)=π⋅lima→∞(1−1a)=π

A=2π∫1a1x1+(−1x2)2−−−−−−−−−−−√dx>2π∫1adxx=2πln(a)

lima→∞A≥lima→∞2πln(a)=∞

但是反过来的情况，即表面积有限，而体积无限的情况，也就是所谓的Gabriel’s horn逆现象，是不存在的。——实际上，众所周知的是表面积一定的形状中，球形体积最大。

Gabriel’s horn现象不仅存在于表面积/体积中，也存在于长度/面积中，即所谓的无限长海岸线问题。对此的进一步研究，开拓了数学中的分形几何领域。

函数连续性

函数连续性本质上是刻画函数在自变量变化的情况下，函数值变化的稳定程度。

连续函数（Continuous function）

∀x∈I∀ϵ>0∃δ>0∀y∈I;|x−y|<δ⇒|f(x)−f(y)|<ϵ

连续函数有很多种等价定义，为了方便和之后的一致连续进行对比，这里选用量词（Quantifier）逻辑的定义。

这个定义实际上是个Nest定义。以 ∃ 为界，整个Quantifier被分成3部分：定值、存在变量、变量。上边的例子实际上是说：在给定 x,ϵ 的情况下，存在 δ ，对所有y，结论都成立。

因为x不变，所以这实际上是个定点连续的条件。因此，这种连续又叫做Pointwise continuity。

通俗的说法：f的函数曲线在区间内没有断点。

一致连续（Uniform continuity）

∀ϵ>0∃δ>0∀x,y∈I;|x−y|<δ⇒|f(x)−f(y)|<ϵ

Uniform continuity比Pointwise continuity要严格一些，因为x,y都是变量。

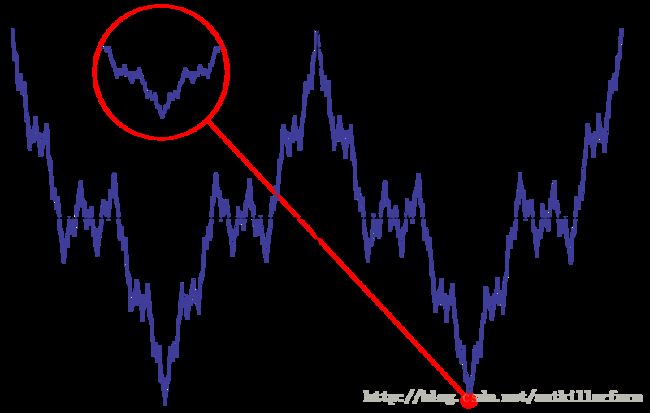
Uniform continuity的形象解释如下所示：

上图中蓝框和红框的顶部和底部用粗线表示，在方框的运动过程中，红线始终没有穿过方框的顶部或底部，所以它是Uniform continuity的，而蓝线不是。

f(x)=1x 不是Uniform continuity的最大原因在于 x→0,f(x)→∞ ，由于值域没有上界，因此，对于给定的 δ ， ϵ 也是没有上界的。

但如果定义域限定为闭区间，则值域必有界。这时，Uniform continuity和Pointwise continuity是等价的。

绝对连续（Absolute continuity）

∀ε>0∃δ>0∀(xk,yk)∈I;∑k(yk−xk)<δ⇒∑k|f(yk)−f(xk)|<ε

Absolute continuity不仅要求整个函数满足Uniform continuity，而且任意子区间也要满足该条件。因此，Absolute continuity比Uniform continuity更严格。

Lipschitz连续

∀x1,x2∈I;|f(x1)−f(x2)|≤K|x1−x2|,K>0 is const

注：Rudolf Otto Sigismund Lipschitz，1832～1903，德国数学家，先后就读于柯尼斯堡大学和柏林大学，导师Dirichlet。波恩大学教授。

Lipschitz连续的直观图示如上所示。该曲线上的所有点的切线斜率的绝对值

≤K

。

易知，Lipschitz continuity比Absolute continuity更严格。

连续可微

这个的定义比较简单：函数的导数是连续的。直观来说就是：函数曲线光滑，没有尖。

由“闭区间的连续函数必有界”可知，Continuously differentiable一定是Lipschitz continuity的。

综上：

Continuously differentiable⊆Lipschitz continuous⊆Absolute continuity⊆uniformly continuous=continuous

需要注意，这些结论只在闭区间成立。比如 f(x)=x2 是连续可微的，但却不是一致连续的。因此又有Local Uniform continuity之类的说法。

Weierstrass Function

Karl Theodor Wilhelm Weierstrass，1815～1897，德国数学家，被誉为“现代分析之父”。
青年时代，Weierstrass被父亲送到波恩大学学习法律和商业，然而他对此根本不感兴趣，精力都花到数学上了，这直接导致离开大学时，没有拿到学位。
此后经过努力，他获得了一份中学数学教师的职位。他30～40岁的时光，就是在两所不知名的中学度过的。
所幸，他的努力没有白费。1854年，他获得格尼斯堡大学荣誉博士学位。此后先后任教于柏林工业大学和柏林洪堡大学。
他的博士学生知名的有：集合论创始人Georg Cantor，世界历史上第一位数学女博士Sofia Kovalevskaya和Hermann Schwarz（没错就是提出Cauchy–Schwarz inequality的那位）。

事实上，本文中使用的 ε−δ 定义，就是Weierstrass的成果。Weierstrass首次采用数学的方式定义极限，取代了之前Newton的物理或几何式的极限定义。

物理或几何式的极限定义有着直观的优势，但不够严格，Weierstrass Function就是最好的反例。

上图是Weierstrass Function图像。它是一类处处连续而处处不可导的实值函数，其表达式为：

f(x)=∑n=0∞ancos(bnπx)

其中， 0<a<1 ，b是奇数，且 ab>1+32π 。最小的满足该条件的值是 b=7 。

一般人会直觉上认为连续的函数必然是近乎可导的。即使不可导，所谓不可导的点也必然只占整体的一小部分。根据Weierstrass在他的论文中所描述，早期的许多数学家，包括高斯，都曾经假定连续函数不可导的部分是有限或可数的。这可能是因为直观上想象一个连续但在不可数个点上不可导的函数是很困难的事。

Weierstrass Function的出现（1872年）说明了所谓的“病态”函数的存在性，改变了当时数学家对连续函数的看法。

Weierstrass Function也被视为第一个分形函数（尽管分形（Fractal）的概念出现的相当晚（1973年），差不多过了整整一个世纪。）：将Weierstrass Function在任一点放大，所得到的局部图都和整体图形相似。因此，无论如何放大，函数图像都不会显得更加光滑，也不存在单调的区间。

参考：

https://wenku.baidu.com/view/21877fea551810a6f524868c.html

一个反例处处连续处处不可导的函数

函数连续性和神经网络

理论上说，多层神经网络只要有足够的深度和宽度，就可以任意逼近任意连续函数。（严格的说，这里的连续函数必须是Borel可测函数。）

然而从网络训练的角度来说，只有Lipschitz连续的函数才一定会收敛，否则的话，可能会出现梯度爆炸的情况。

参考

https://www.zhihu.com/question/32201415

函数连续和一致连续有什么区别？开区间上的连续函数不一定是一致连续的，为什么？

https://zhuanlan.zhihu.com/p/27554191

非凸优化基石：Lipschitz Condition

http://www.cnblogs.com/flywithyou/p/4135562.html

Lipschitz连续

https://www.zhihu.com/question/62554985

神经网络的上同调理论

http://tech.scichina.com:8082/sciE/CN/abstract/abstract404403.shtml

神经网络的本质逼近阶

http://www.doc88.com/p-2337088655000.html

神经网络的函数逼近理论

https://zhuanlan.zhihu.com/p/25590725

神经网络为什么能够无限逼近任意连续函数？

https://max.book118.com/html/2015/0401/14126427.shtm

浅谈Borel可测函数及其性质