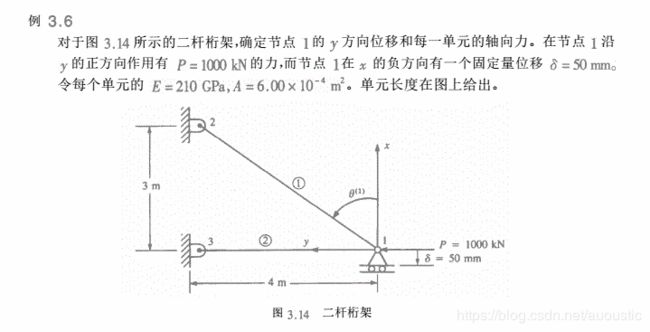
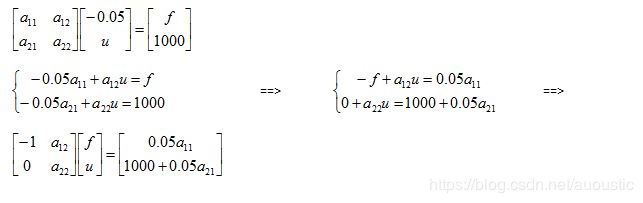Python 进行有限元分析 -- 有限元方法基础教程 （第五版）（例题3.6）

在《有限元方法基础教程》（第五版）中，第三章是桁架问题。

这里再重新强调一遍有限元分析的基本步骤（重要的事情我们要经常说）：

step 1： 离散和选择单元类型。

step 2: 选择位移函数。（位移函数一般都是多项式函数，一般都选线性，类似于y = ax +b .除非特别情况，一般都是选择这个函数）

step 3: 写出力和位移的关系，或者应力/应变关系。

step 4: 得到单元刚度矩阵。

step 5: 组合总体刚度矩阵。

step 6: 带入边界条件。

step 7: 求解未知量（一般是求解出力和位移）。以及自己想要获取的量（有时候让求解应力和应变）。

以上便是直接刚度法来进行有限元求解的步骤了。

接下来，我们便开始通过Python来编写计算本题的有限元程序。

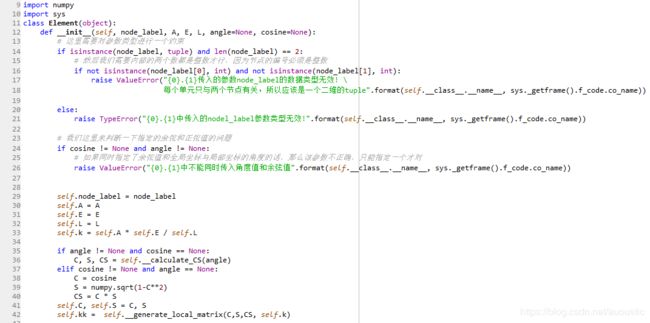
第一步： 我们创建一个单元类，其实例用来表示单元，单元的基本信息包括：A（横截面积），E（杨氏模量）,L(单元的长度)，angle(局部坐标系相对于全局坐标系所转过的角度), <最重要的特性><与单元相关的节点的编号i， j>(因为节点编号是我们将单元刚度矩阵组合到总体刚度矩阵中去的时候的关键因素，所以这个特性非常重要，而且对应的顺序也不能变)。

这是我们的单元类，在Python中__init__()函数就类似于java中的类的构造器，我们可以注意到这里传入的参数有6个，第一个Node_label是与当前单元有关系的节点的编号所组成的tuple。我们在本函数的代码部分，对部分参数的类型进行限制，这里强制要求传入的Node_label必须是tuple类型，而且必须是2个元素的tuple。之所以这么设置是因为当前的单元是一个杆单元，只有两端的节点与其有关系。

2~4参数分别为：横截面接，杨氏模量，单元长度。

对于第五个参数angle设置为了None, 并且第六个参数cosine也设置为了None.关于此参数的说明请见: 函数的参数 - 廖雪峰的官方网站 . 之所以这么设置，是因为我们注意到对于本题，求解局部坐标相对于全局坐标的偏转角度的正余弦要比求角度方便的多，于是我们在这里添加了直接设置余弦和正弦的参数，并且我们也不想抛弃掉设置angle参数的功能，因为在某些问题中，可能设置角度更为方便。

第二步： 我们先来生成单元实例，通过实例我们再来判断一下刚度矩阵的组合方式。

我们通过一个列表来将存储所有的单元。（如果查看过Abaqus的Python Reference的话，你会发现所有的不管是单元还是节点都会存在在对应的单元仓库和节点仓库，类型是list）

第三步： 我们再来组合对应的总体刚度矩阵

第四步： 带入对应的边界条件

这里一定要注意，如果不设置dtype的话，整个array会默认为全部元素为字符串，下面根本无法进行计算。

第五步： 计算对应的未知量。

这里要注意，力/位移关系满足： F=KU; 那么U中为0的元素将不会对F中的内容有任何贡献。那么剩下的U中只有前两个元素。而且我们要再来得到F中的前两个元素，但是这里边U中有一个未知量，F中有一个未知量，所以我们无法通过矩阵的操作来实现方程组的求解。为了能使本题采用矩阵的相乘法来得到未知量的值：

我们需要做以下处理： 因为在排除掉U中的0元素之后，剩下的是两个方程，由两个方程来确定两个未知量，是完全没有问题的。

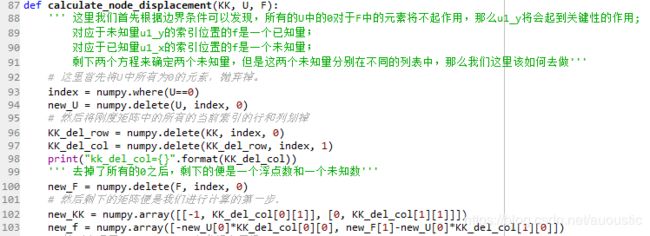
其对应的算法实现如下所示：

接下来便可以通过矩阵的方式来求解对应的未知量了。

然后再接下来，便将所计算出来的u写入到原位移矩阵U中，然后再将通过原位移矩阵U，跟刚度矩阵K的乘积来得到力矩阵。

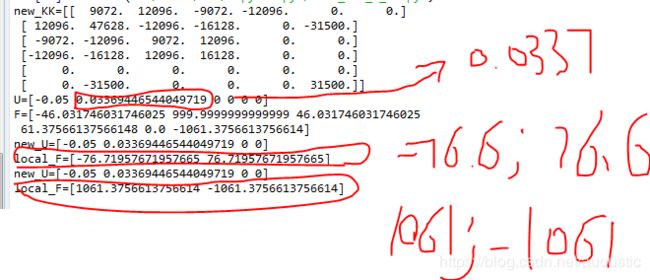
到此，要计算的位移矩阵和力矩阵便完全计算得到了，接下来便是可以来计算对应的局部坐标系下的力。

到此，我们可以对比显示的结果和书本中给出的例题的结果：

赞助一点钱.