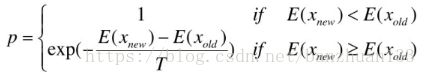启发式算法解TSP问题

一、前言

       旅行商问题(TravelingSalesmanProblem，TSP)是一个经典的组合优化问题。经典的TSP可以描述为：一个商品推销员要去若干个城市推销商品，该推销员从一个城市出发，需要经过所有城市后，回到出发地。应如何选择行进路线，以使总的行程最短。由于该问题的可行解是所有顶点的全排列，随着顶点数的增加，会产生组合爆炸，它是一个NP完全问题。早期的研究者使用精确算法求解该问题，常用的方法包括：分枝定界法、线性规划法、动态规划法等。但是，随着问题规模的增大，精确算法将变得无能为力，因此，在后来的研究中，国内外学者重点使用近似算法或启发式算法，主要有遗传算法、模拟退火法、蚁群算法、禁忌搜索算法、贪婪算法和神经网络等。

二、模拟退火法

       模拟退火算法的思想借鉴于固体的退火原理，当固体的温度很高的时候，内能比较大，固体的内部粒子处于快速无序运动，当温度慢慢降低的过程中，固体的内能减小，粒子的慢慢趋于有序，最终，当固体处于常温时，内能达到最小，此时，粒子最为稳定。模拟退火算法便是基于这样的原理设计而成。其流程可以概括如下

• 随机产生一个初始访问序列，并计算响应的行程和，保存为当前最佳路径。
• 设置初始温度T(0)，终止温度T(min)，降温系数a。
  
• while(T>T(min))，在当前的最优值，按照某一邻域函数，产生新的路径，并计算新路径的路径和。如果优于最优值，则更迭最优决策，如果不是，按照Metropolis法则选择是否更新。
• 降温，达到循环终止条件则跳出。
• Metropolis法则

可以避免局部陷阱

• matlab代码

%C表示初始城市坐标
C=[1,2;70,90;80,60;10,100;800,200;800,100;90,80;200,600;230,4;500,90];
n=length(C);
D=zeros(n,n);%D表示完全图的赋权邻接矩阵
%计算距离矩阵
for i=1:n
    for j=i:n
        if i~=j
            D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;
        else
            D(i,j)=eps;      %i=j时不计算，应该为0，用eps（浮点相对精度）表示
        end
        D(j,i)=D(i,j);   %对称矩阵
    end
end
%初始化
path_best=[];
T=3000;
delta_T=0.98; %降温系数
p=randperm(n);
dist=0.0;
path_best=p;
for i=1:n-1
    dist=dist+D(p(i),p(i+1));
end
dist=dist+D(p(1),p(n));
dist_best=dist;
%降温循环过程
while(T>1e-8)
    %采用最简单的邻域取法，直接对换其中两个节点的城市
    x=ceil(n*rand());
    y=ceil(n*rand());
    while(x==y)
        x=ceil(n*rand());
        y=ceil(n*rand());
    end
    z=p(x);
    p(x)=p(y);
    p(y)=z;
    for i=1:n-1
        dist=dist+D(p(i),p(i+1));
    end
    dist=dist+D(p(1),p(n));    
    if(distb)  %概率大于产生随机数时则采用
            dist_best=dist;
            path_best=p;  
        end
    end
    T=T*delta_T;
end
%画图输出结果
subplot(1,1,1) 
scatter(C(:,1),C(:,2));
hold on
plot([C(path_best(1),1),C(path_best(n),1)],[C(path_best(1),2),C(path_best(n),2)],'g')
hold on
for ii=2:n
plot([C(path_best(ii-1),1),C(path_best(ii),1)],[C(path_best(ii-1),2),C(path_best(ii),2)],'g')
hold on
end
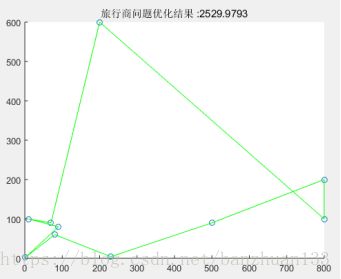
title(['旅行商问题优化结果 :',num2str(dist_best)])

• 输出结果

                              

从结果可以看出启发式算法的特点，由于是经验算法，结果并不是严格意义上的最优解，因此具有一定的随机性，但只要迭代次数足够多，总可以收敛到最优解附近。

三、遗传算法

       遗传算法（GA）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。遗传算法是从代表问题可能潜在的解集的一个种群开始的，而一个种群则由经过基因编码的一定数目的个体(individual)组成。每个个体实际上是染色体带有特征的实体。由于仿照基因编码的工作很复杂，我们往往进行简化，如二进制编码，初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代演化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度大小选择个体，并借助于自然遗传学的遗传算子进行组合交叉和变异，产生出代表新的解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码，可以作为问题近似最优解。

其主要流程如下：

• 初始化参数，包括种群数量，繁衍代数，变异概率，城市坐标，染色体长度等。
• 计算距离矩阵，生成初始种群。
• 当迭代次数不满足时，执行杂交循环。
• 杂交包括选择，交叉，变异三个过程。选择的方法有很多种，此处采用最简单的最优者生存的方法，即目标函数前60%的个体可以顺利繁衍后代。也可以采用轮盘赌的方法，所有个体均可以繁衍后代，但是目标值越优的个体被挑选的概率越大。交叉的过程是随机生成染色体长度内的两个整数值，并将选择出的两个个体的该段染色体交叉互换。变异按照一定概率进行，当生成的随机数大于变异概率时则进行变异。
• 更新种群，采用“精英保留”的策略。即在种群数量一定的情况下，每次总是留下目标最优的群体。继续循环直到满足跳出条件。

matlab代码如下：

%主程序部分
NUM=20;%种群大小
GEN=100;%代数
P=0.7;%变异概率
C=[1,2;70,90;80,60;10,100;800,200;800,100;90,80;200,600;230,4;500,90];%城市坐标
n=length(C);
D=zeros(n,n);%D表示完全图的赋权邻接矩阵
%计算初始距离矩阵
for i=1:n
    for j=i:n
        if i~=j
            D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;
        else
            D(i,j)=eps;      %i=j时不计算，应该为0，用eps（浮点相对精度）表示
        end
        D(j,i)=D(i,j);   %对称矩阵
    end
end
group=zeros(NUM,n);%种群
dist=zeros(NUM,1);%路径和

%生成初始种群
for i=1:NUM
    group(i,:)=randperm(n);
    for j=1:n-1
        dist(i)=dist(i)+D(group(i,j),group(i,j+1));
    end
    dist(i)=dist(i)+D(group(i,1),group(i,n));
end
res=[group,dist];
res=sortrows(res,n+1);%按路径和排序
path_best=res(1,1:n);%保存最优路径和最小路径和
dist_min=res(1,n+1);
M=floor(NUM*0.6);%0.6为适应度系数，即假设60%为适应并繁衍的种群

%执行杂交操作
for i=1:GEN         
    res=yichuan(res,M,n,D,P,NUM);
    path_best=res(1,1:n);
    dist_min=res(1,n+1);
end
%输出结果
subplot(1,1,1) 
scatter(C(:,1),C(:,2));
hold on
plot([C(path_best(1),1),C(path_best(n),1)],[C(path_best(1),2),C(path_best(n),2)],'g')
hold on
for ii=2:n
plot([C(path_best(ii-1),1),C(path_best(ii),1)],[C(path_best(ii-1),2),C(path_best(ii),2)],'g')
hold on
end
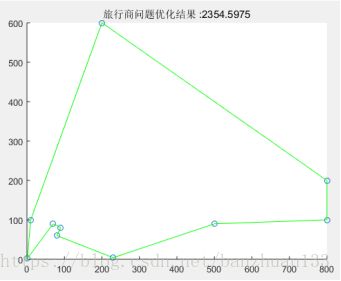
title(['旅行商问题优化结果 :',num2str(dist_min)])

遗传函数部分

function [res]=yichuan(res,M,n,D,P,NUM)
%res为储存路径和总距离的矩阵，M为适应生存的种群数，n为染色体长度，D为距离矩阵，P是变异概率，NUM为种群数
group=res(1:M,1:n);
dist=res(1:M,n+1);
list=randperm(M);%随机生成父本和母本序列
for j=1:2:M-1
    [group(list(j),:),group(list(j+1),:)]=jiaocha(group(list(j),:),group(list(j+1),:),n,P);
    dist(j)=cal_dist(group(j,:),D,n);
    dist(j+1)=cal_dist(group(j+1,:),D,n); 
end
R=zeros(2*M,n+1);
R=[res;group,dist];
R=sortrows(R,n+1);
res=R(1:NUM,:);%精英保留
end

%交叉，变异
function [r1,r2]=jiaocha(r1,r2,n,P)
    a=randperm(n,2);
    l=min(a);
    m=max(a);
    while(l==m)
        a=randperm(10,2);
        l=min(a);
        m=max(a);
    end    
    a1=r1;
    a2=r2;
    %交换中间部分，并替换重复出现的染色体
    for k=l:m
        r1(k)=a2(k);
        r2(k)=a1(k);
        x=find(a1==r1(k));
        y=find(a2==r2(k));
        r1(x)=a1(k);
        r2(y)=a2(k);
        a1=r1;
        a2=r2;
    end
    %随机数大于变异概率则变异
    if(rand()>P)
        q=randperm(n,2);
        s=r1(q(1));
        r1(q(1))=r1(q(2));
        r1(q(2))=s;
    end
    if(rand()>P)
        q=randperm(n,2);
        s=r2(q(1));
        r2(q(1))=r2(q(2));
        r2(q(2))=s;
    end
end

%计算路径和
function [dist]=cal_dist(path,Dist,n)
    dist=0;
    for k=1:n-1
        dist=dist+Dist(path(k),path(k+1));
    end
    dist=dist+Dist(path(1),path(n));
        
end

输出结果

四、蚁群算法

       最早是由Marco Dorigo等人在1991年提出，基于信息正反馈原理。蚂蚁视觉十分不发达，却能够在没有任何提示的情况下找到食物源到巢穴的最短路径，并在周围环境发生变化后，自适应地搜索新的最佳路径。原因是蚂蚁在寻找食物源的时候，能在其走过的路径上释放信息素，当一些路径上通过的蚂蚁越来越多，信息素也越来越多，蚂蚁选择该路径的概率也就越大。对单个蚂蚁来说，它没有找到最短路径，但对整个蚁群来说，却达到了寻找最优路径的客观效果。

其算法流程如下：

• 对相关参数进行初始化，包括蚁群规模、信息素因子、启发函数因子、信息素挥发因子、信息素常数、最大迭代次数等，以及将数据读入程序，并进行预处理：比如将城市的坐标信息转换为城市间的距离矩阵。 
  
• 随机将蚂蚁放于不同出发点，对每个蚂蚁计算其下个访问城市，直到有蚂蚁访问完所有城市。 
  
• 计算各蚂蚁经过的路径长度LkLk，记录当前迭代次数最优解，同时对路径上的信息素浓度进行更新。
  
• 判断是否达到最大迭代次数，若否，继续循环。
  
• 输出结果，并根据需要输出寻优过程中的相关指标，如运行时间、收敛迭代次数等。
  

代码如下：

%%第一步：变量初始化
C=[1,2;70,90;80,60;10,100;800,200;800,100;90,80;200,600;230,4;500,90];

NC_max=200;
m=18;
Alpha=1;
Beta=5;
Rho=0.5;
Q=1;
n=size(C,1);%n表示问题的规模（城市个数）
D=zeros(n,n);%D表示完全图的赋权邻接矩阵
for i=1:n
    for j=i:n
        if i~=j
            D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;
        else
            D(i,j)=eps;      %i=j时不计算，应该为0，但后面的启发因子要取倒数，用eps（浮点相对精度）表示
        end
        D(j,i)=D(i,j);   %对称矩阵
    end
end
Eta=1./D;          %Eta为启发因子，这里设为距离的倒数
Tau=ones(n,n);     %Tau为信息素矩阵
Tabu=zeros(m,n);   %存储并记录路径的生成
NC=1;               %迭代计数器，记录迭代次数
R_best=zeros(NC_max,n);       %各代最佳路线
L_best=inf.*ones(NC_max,1);   %各代最佳路线的长度
L_ave=zeros(NC_max,1);        %各代路线的平均长度
 
while NC<=NC_max        %停止条件之一：达到最大迭代次数，停止
%%第二步：将m只蚂蚁放到n个城市上
Randpos=[];   %随即存取
for i=1:(ceil(m/n))  %向上取整
    Randpos=[Randpos,randperm(n)];  %并成一列
end
Tabu(:,1)=(Randpos(1,1:m))';    %第一行的1到m列元素
 
%%第三步：m只蚂蚁按概率函数选择下一座城市，完成各自的周游
for j=2:n     %所在城市不计算
    for i=1:m    
        visited=Tabu(i,1:(j-1)); %记录已访问的城市，避免重复访问
        J=zeros(1,(n-j+1));       %待访问的城市
        P=J;                      %待访问城市的选择概率分布
        Jc=1;
        for k=1:n
            if length(find(visited==k))==0   %开始时置0，找出未访问的城市,find返回的是位置
                J(Jc)=k;
                Jc=Jc+1;                         
            end
        end
%下面计算待选城市的概率分布
        for k=1:length(J)
            P(k)=(Tau(visited(end),J(k))^Alpha)*(Eta(visited(end),J(k))^Beta);
        end
        P=P/(sum(P));
        %按概率原则选取下一个城市
%         Pcum=cumsum(P);     %cumsum返回行和和列和，sum返回列和
%         Select=find(Pcum>=rand); %若计算的概率大于原来的就选择这条路线
        Select=max(P);
        Select=find(P==Select);
        to_visit=J(Select(1));
        Tabu(i,j)=to_visit;
    end
end
if NC>=2
    Tabu(1,:)=R_best(NC-1,:);
end
 
%%第四步：记录本次迭代最佳路线
L=zeros(m,1);     %开始距离为0，m*1的列向量
for i=1:m
    R=Tabu(i,:);
    for j=1:(n-1)
        L(i)=L(i)+D(R(j),R(j+1));    %原距离加上第j个城市到第j+1个城市的距离
    end
    L(i)=L(i)+D(R(1),R(n));      %一圈，回到起点
end
L_best(NC)=min(L);           %最佳距离取最小
pos=find(L==L_best(NC));
R_best(NC,:)=Tabu(pos(1),:); %此轮迭代后的最佳路线
L_ave(NC)=mean(L);           %此轮迭代后的平均距离
NC=NC+1                      %迭代继续
 
 
%%第五步：更新信息素
Delta_Tau=zeros(n,n);        %开始时信息素为n*n的0矩阵
for i=1:m
    for j=1:(n-1)
        Delta_Tau(Tabu(i,j),Tabu(i,j+1))=Delta_Tau(Tabu(i,j),Tabu(i,j+1))+Q/L(i);          
        %此次循环在路径（i，j）上的信息素增量
    end
    Delta_Tau(Tabu(i,n),Tabu(i,1))=Delta_Tau(Tabu(i,n),Tabu(i,1))+Q/L(i);
    %此次循环在整个路径上的信息素增量
end
Tau=(1-Rho).*Tau+Delta_Tau; %考虑信息素挥发，更新后的信息素
Tabu=zeros(m,n);             %%直到最大迭代次数
end
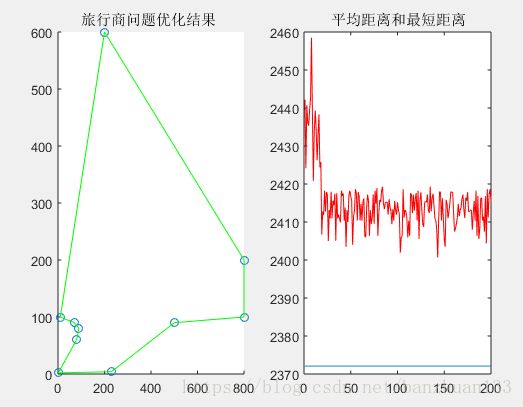
%%第六步：输出结果
Pos=find(L_best==min(L_best)); %找到最佳路径（非0为真）
Shortest_Route=R_best(Pos(1),:) %最大迭代次数后最佳路径
Shortest_Length=L_best(Pos(1)) %最大迭代次数后最短距离
subplot(1,2,1)                  %绘制第一个子图形
DrawRoute(C,Shortest_Route)     %画路线图的子函数
subplot(1,2,2)                  %绘制第二个子图形
plot(L_best)
hold on                         %保持图形
plot(L_ave,'r')
title('平均距离和最短距离')     %标题
end


function DrawRoute(C,R)
N=length(R);
scatter(C(:,1),C(:,2));
hold on
plot([C(R(1),1),C(R(N),1)],[C(R(1),2),C(R(N),2)],'g')
hold on
for ii=2:N
plot([C(R(ii-1),1),C(R(ii),1)],[C(R(ii-1),2),C(R(ii),2)],'g')
hold on
end
title('旅行商问题优化结果 ')
end

输出结果