题面如下:
X 国王有一个地宫宝库,是 n×m个格子的矩阵,每个格子放一件宝贝,每个宝贝贴着价值标签。
地宫的入口在左上角,出口在右下角。
小明被带到地宫的入口,国王要求他只能向右或向下行走。
走过某个格子时,如果那个格子中的宝贝价值比小明手中任意宝贝价值都大,小明就可以拿起它(当然,也可以不拿)。
当小明走到出口时,如果他手中的宝贝恰好是 kk 件,则这些宝贝就可以送给小明。
请你帮小明算一算,在给定的局面下,他有多少种不同的行动方案能获得这 kk 件宝贝。
输入格式
第一行 3 个整数,n,m,k,含义见题目描述。
接下来 n 行,每行有 m个整数 Ci用来描述宝库矩阵每个格子的宝贝价值。
输出格式
输出一个整数,表示正好取 k 个宝贝的行动方案数。
该数字可能很大,输出它对 1000000007取模的结果。
数据范围
1≤n,m≤50
1≤k≤12
0≤Ci≤12
输入样例1:
2 2 2
1 2
2 1
输出样例1:
2
输入样例2:
2 3 2
1 2 3
2 1 5
输出样例2:
这个题的题目数据范围很小,可以预估是一个维数较多的dp,我最开始的思路如下(虽然这个思路不对,但是AC思路是在这个基础上做了一点很小的调整):
每个点都只能往下或者往右移动,可以选择拿走下面/右面的宝物,也可以不拿,如果拿了,k维度上升一层,否则仍然在这一层,同时维护当前手中最大的物品重量就可以了
枚举顺序和Lintcode114 Unique Paths等走迷宫类似的题目的枚举顺序一样,一行行计算即可,只不过多加了一重k的限制
起始点宝物的拾取不能按照上述规则处理,所以在最开始单独给dp[0][0][1]特殊赋值一下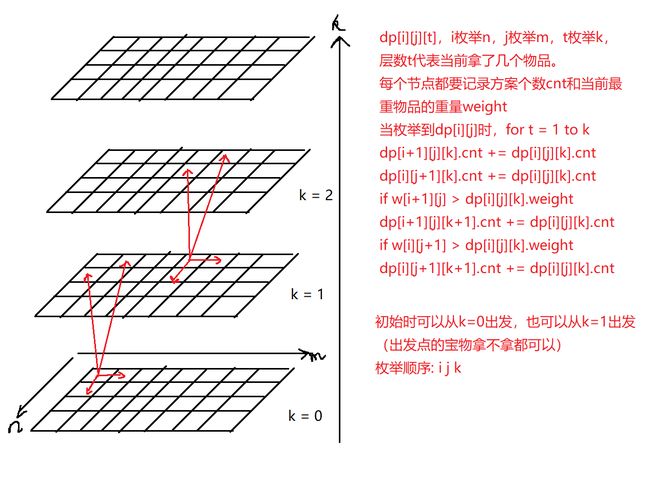
然后开开心心地吃了两发WA,感觉事情不对劲,突然意识到这个手中最大宝物重量不能直接存个最大的,举个例子:3,3,3处有5种走法,最大重量是7;2,3,4处有6种走法,最大重量是9,这两个位置都能来到3,3,4这个位置,虽然方案数看着可以合并,但是他们最大重量是不同的,所以实际上不能直接合并(3,3,4这个点需要记录着有5种走法的最大重量是7;有6种走法的最大重量是9,不然面临一个重量为8的宝物,你是没办法处理的),所以。。我们还要再加一层数组,把它变成四维数组,其中第四维表示最大重量,这样我们的dp数组表示的含义就变成了下面这样:
dp[i][j][t][p]表示位置在i,j处,当前已经拿了t个物品,这些物品中的最大重量是p的方案个数有多少种,转移方程没太大变化,就是加了一个第四维的循环
AC代码如下:
#include#include #include #include using namespace std; #define modulus 1000000007 long long arr[55][55][13][14]; int weight[55][55]; int main() { int n, m, k; cin >> n >> m >> k; for(int i = 0; i < n; i++) { for(int j = 0; j < m; j++) { int temp; scanf("%d", &temp); weight[i][j] = temp + 1; } } arr[0][0][0][0] = 1; arr[0][0][1][weight[0][0]] = 1; for(int i = 0; i < n; i++) { for(int j = 0; j < m; j++) { for(int t = 0; t <= k; t++) { for(int p = 0; p < 14; p++) { arr[i+1][j][t][p] += arr[i][j][t][p]; arr[i+1][j][t][p] %= modulus; arr[i][j+1][t][p] += arr[i][j][t][p] % modulus; arr[i][j+1][t][p] %= modulus; if(weight[i+1][j] > p) { arr[i+1][j][t+1][weight[i+1][j]] += arr[i][j][t][p]; arr[i+1][j][t+1][weight[i+1][j]] %= modulus; } if(weight[i][j+1] > p) { arr[i][j+1][t+1][weight[i][j+1]] += arr[i][j][t][p]; arr[i][j+1][t+1][weight[i][j+1]] %= modulus; } } //cout << "i=" << i <<" j=" << j << " t=" << t << endl; //cout << arr[i][j][t] << endl; } } } int sum = 0; for(int i = 0; i < 14; i++) { sum = sum + arr[n-1][m-1][k][i]; sum %= modulus; } cout << sum << endl; return 0; }