大部分机器学习模型处理的都是特征,是实际工作中最耗时的一部分。大部分情况下,收集到的数据需要经过预处理后才能被后续的机器学习算法所使用。
一、数据预处理包括以下几个步骤
1、数据过滤
比如用户ID是一个唯一值,当出现两个相同的用户ID就需要过滤掉一个。
2、处理数据缺失
如果有500个样本,其中第230个样本的某个数据缺失,我们可以考虑使用总体样本的平均值、中位数(Mediam,所有数据值从大到小排序最中间的那个值)、众数(Mode,数据中出现次数最多的那个值) 来代替该样本的缺失的值。
当特征是离散型数据的时候,多数用众数来填补缺失值。比如一组数据为(1,1,1,1,NaN,0,1,1) 用什么值来填充NaN比较合适呢?也许这组数据体现的是姓别(0=男、1=女),显然使用中位数或均值都不能代表样本的特性,因此选择众数。
3、处理可能的异常值、错误值
手机号的数据中出现了一个中文,那么考虑将这组样本删除。
4、合并多个数据源数据
租房预测模型中,待租房屋的特征中包含长度和宽度,那么如果将这两组数据合并成面积或许更能体现特征的价值。
二、数据预处理的方法
1、哑编码
功能:分类编码,将非数值型的特征值转化为数值型的数据。
描述:假设变量的取值有k个,如果对这些值用1到k编号,则可用k的向量来表示一个变量的值。在这样的向量里,该取值所对应的需要所在的元素为1,其他元素为0。
| 样本/特征 | T1 | T2 | T3 |
|---|---|---|---|
| R1 | A | 1 | 2 |
| R2 | A | 2 | 3 |
| R3 | B | 3 | 3 |
| R4 | C | 2 | 2 |
| R5 | C | 1 | 2 |
T1特征有三种分类:A、B、C,但无法确定哪种分类更好。在T1的基础上生成三个新的特征 T1-A 、T1-B 、T1-C。于是在原有的T1维度上进行了扩张,将1维变成了3维。
| 向量/类型 | T1-A | T1-B | T1-C |
|---|---|---|---|
| A | 1 | 0 | 0 |
| B | 0 | 1 | 0 |
| C | 0 | 0 | 1 |
生成的新数据集删除了原本的T1特征,新增了 T1-A 、T1-B 、T1-C特征:
| 样本/特征 | T1-A | T1-B | T1-C | T2 | T3 |
|---|---|---|---|---|---|
| R1 | 1 | 0 | 0 | 1 | 2 |
| R2 | 1 | 0 | 0 | 2 | 3 |
| R3 | 0 | 1 | 0 | 3 | 3 |
| R4 | 0 | 0 | 1 | 2 | 2 |
| R5 | 0 | 0 | 1 | 1 | 2 |
哑编码是一个将数据集从低维变成高维的过程,是对数据的一种扩充。但该方法既有正向的影响也有负向的影响,具体的问题在后续欠拟合与过拟合的问题中进一步叙述。
PS: 大家可以思考一下,如果此时将T1-C删除了,会对结果有什么影响?提示:多重共线性。其实删除了T1-C对于结果没有影响,因为10、01、00即可表示三种不同的类型。后续哑编码会用得比较多,希望大家能够看明白。
2、文本数据提取
词袋法(BOW):将文本当作一个无序的数据集合,文本特征可以采用文本中的词条T进行体现,那么文本中出现的所有词条及其出现的次数就可以体现文档的特征。
词袋法有几个关键点:
1、每个公司的词库是不同的,词条T可以理解为词组,比如“人工智能”、“爬虫”、“机器学习”,“大数据” 这词条出现得多了,可以默认文章属于IT类的,更细分可以规定为AI分类。
2、不是所有的词条都是有意义的,比如“我”,“的”,“了” 这些对于文章内容是毫无意义的词组。再比如说:“刀”、“剑” 在武侠小说中出现几乎没有意义,但在新闻里如果出现了就变得很有意义。
所以词频的重要性,有时候和出现的频率成正比,有时候成反比。于是引入了TF-IDF算法。
TF-IDF:
1、TF:词频。指某个词条出在文本中的次数,一般会将其进行归一化操作 (该词条数量/该文档中所有词条的数量)。
2、IDF:逆向文件频率。指一个词条重要性的度量= 总文件数/包含词语的文件数。有时候得到的商还会取对数操作。
3、TF-IDF = TF*IDF
举个栗子:
文档1的内容:A(2)、B(1)、C(3)、D(9)、E(1)
文档2的内容:A(1)、B(5)、C(2)、D(10)
BoW模型:
| 样本/特征 | A | B | C | D | E |
|---|---|---|---|---|---|
| 文档1 | 2 | 1 | 3 | 9 | 1 |
| 文档2 | 1 | 5 | 2 | 10 | 0 |
TF(A|文档1的总词条) = 2/(2+1+3+9+1)=1/8
...
TF(E|文档2的总词条) = 0/(1+5+2+10)=0/18=0
IDF(A) = IDF(B) = IDF(C) = IDF(D) = 2/2
IDF(E) = 2/1
A、B、C、D字条在文档1和文档2中都有出现,而E词条只在文档2中出现。
最后计算 TF*IDF 得到模型:
| 样本/TF-IDF(X) | A | B | C | D | E |
|---|---|---|---|---|---|
| 文档1 | 1/8 | 1/16 | 3/16 | 9/16 | 1/8 |
| 文档2 | 1/18 | 5/18 | 1/9 | 5/9 | 0 |
3、傅立叶变换。
处理图像或音频(像素、声波、音频、振幅)
4、数值数据转换为类别数据,以减少变量的值
比如:年龄分段
1.童年---0岁—6岁。
2.少年---7岁—17岁。
3.青年---18岁—40岁。
4.中年---41—65岁。
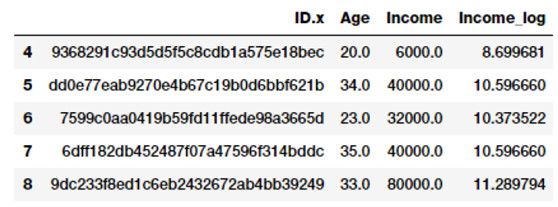
5、数值数据进行转换:对数转换
这组数据斜率非常大,需要利用统计或数学变换来减轻数据分布倾斜的影响。使原本密集的区间的值尽可能的分散,原本分散的区间的值尽量的聚合。
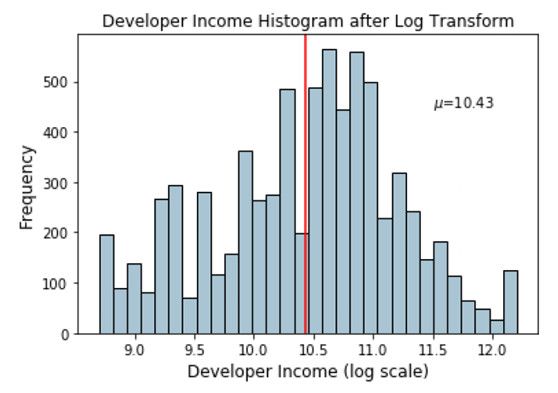
Log变换通常用来创建单调的数据变换。它的主要作用在于帮助稳定方差,始终保持分布接近于正态分布并使得数据与分布的平均值无关。
y=logc(1+λx)。λ 通常设置为1,c通常设置为变换数据的最大值。
Log变换倾向于拉伸那些落在较低的幅度范围内自变量值的范围,压缩或减少较高幅度范围内的自变量值的范围。从而使得倾斜分布尽可能的接近正态分布。
对数转换部分参考文献:
https://www.leiphone.com/news/201801/T9JlyTOAMxFZvWly.html